[Computer Vision]实验二:图像特征点提取
目录
一、实验内容
二、实验过程及结果
2.1 Harris角点检测
2.2 SIFT算法
三、实验小结
一、实验内容
- 采用Harris与SIFT分别提取特征点及对应的描述子,对比两者的区别(特征点数量、分布、描述子维度、图像变化对二者的影响等)
- 利用特征匹配算法实现两幅相近图像的特征匹配,打印匹配点数量级结果
二、实验过程及结果
2.1 Harris角点检测
以下是Harris.py文件
from PIL import Image
from pylab import *
import matplotlib.pyplot as plt
from scipy.ndimage import filters
def compute_harris_response(im,sigma=3):
imx = zeros(im.shape)
filters.gaussian_filter(im, (sigma,sigma), (0,1), imx)
imy = zeros(im.shape)
filters.gaussian_filter(im, (sigma,sigma), (1,0), imy)
Wxx = filters.gaussian_filter(imx*imx,sigma)
Wxy = filters.gaussian_filter(imx*imy,sigma)
Wyy = filters.gaussian_filter(imy*imy,sigma)
Wdet = Wxx*Wyy - Wxy**2
Wtr = Wxx + Wyy
return Wdet / Wtr
def get_harris_points(harrisim, min_dist=10, threshold=0.1):
corner_threshold = harrisim.max() * threshold
harrisim_t = (harrisim > corner_threshold) * 1
coords = array(harrisim_t.nonzero()).T
candidate_values = [harrisim[c[0], c[1]] for c in coords]
index = argsort(candidate_values)
allowed_locations = zeros(harrisim.shape)
allowed_locations[min_dist:-min_dist, min_dist:-min_dist] = 1
filtered_coords = []
for i in index:
if allowed_locations[coords[i, 0], coords[i, 1]] == 1:
filtered_coords.append(coords[i])
allowed_locations[(coords[i, 0] - min_dist):(coords[i, 0] + min_dist),
(coords[i, 1] - min_dist): (coords[i, 1] + min_dist)] = 0
return filtered_coords
def plot_harris_points(image, filtered_coords):
figure()
gray()
imshow(image)
plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], '*')
show()
def get_descriptors(image,filtered_coords,wid=5):
desc = []
for coords in filtered_coords:
patch = image[coords[0]-wid:coords[0]+wid+1,coords[1]-wid:coords[1]+wid+1].flatten()
desc.append(patch)
return desc
def match(desc1,desc2,threshold=0.5):
n = len(desc1[0])
d = -ones((len(desc1),len(desc2)))
for i in range(len(desc1)):
for j in range(len(desc2)):
d1 = (desc1[i] - mean(desc1[i])) / std(desc1[i])
d2 = (desc2[j] - mean(desc2[j])) / std(desc2[j])
ncc_value = sum(d1*d2) / (n-1)
if ncc_value > threshold:
d[i,j] = ncc_value
ndx = argsort(-d)
matchscores = ndx[:,0]
return matchscores
def match_twosided(desc1,desc2,threshold=0.5):
matches_12 = match(desc1,desc2,threshold)
matches_21 = match(desc2,desc1,threshold)
ndx_12 = where(matches_12 >= 0)[0]
for n in ndx_12:
if matches_21[matches_12[n]] != n:
matches_12[n] = -1
return matches_12
def appendimages(im1,im2):
rows1 = im1.shape[0]
rows2 = im2.shape[0]
if rows1 < rows2:
im1 = concatenate((im1,zeros((rows2-rows1,im1.shape[1]))),axis=0)
elif rows1 > rows2:
im2 = concatenate((im2,zeros((rows1-rows2,im2.shape[1]))),axis=0)
return concatenate((im1,im2), axis=1)
def plot_matches(im1,im2,locs1,locs2,matchscores,show_below=True):
im3 = appendimages(im1,im2)
if show_below:
im3 = vstack((im3,im3))
imshow(im3)
cols1 = im1.shape[1]
for i,m in enumerate(matchscores):
if m>0:
plot([locs1[i][1],locs2[m][1]+cols1],[locs1[i][0],locs2[m][0]],'c')
axis('off')以下是test.py文件
from pylab import *
from PIL import Image
import harris
import sift
import cv2
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)
def harris_points(im):
harrisim = harris.compute_harris_response(im)
harrisim1 = 255 - harrisim
figure()
gray()
suptitle("Harris")
subplot(2,3,1)
title("test picture")
imshow(im)
subplot(2,3,2)
title("harris response")
imshow(harrisim1)
print (harrisim1.shape)
threshold1 = 0.01
threshold2 = 0.05
threshold3 = 0.1
filtered_coord1 = harris.get_harris_points(harrisim, 6, threshold1)
filtered_coord2 = harris.get_harris_points(harrisim, 6, threshold2)
filtered_coord3 = harris.get_harris_points(harrisim, 6, threshold3)
print (im.shape)
subplot(2, 3, 4)
title("thres=0.01")
imshow(im)
plot([p[1] for p in filtered_coord1], [p[0] for p in filtered_coord1], '+c')
subplot(2, 3, 5)
title("thres=0.05")
imshow(im)
plot([p[1] for p in filtered_coord2], [p[0] for p in filtered_coord2], '+c')
subplot(2, 3, 6)
title("thres=0.1")
imshow(im)
plot([p[1] for p in filtered_coord3], [p[0] for p in filtered_coord3], '+c')
axis('off')
axis('equal')
show()
def harris_match(im1,im2,wid):
harrisim1=harris.compute_harris_response(im1,5)
filtered_coords1=harris.get_harris_points(harrisim1,wid+1)
d1=harris.get_descriptors(im1,filtered_coords1,wid)
harrisim2=harris.compute_harris_response(im2,5)
filtered_coords2=harris.get_harris_points(harrisim2,wid+1)
d2=harris.get_descriptors(im2,filtered_coords2,wid)
print("starting harris matching")
matches=harris.match_twosided(d1,d2)
figure()
gray()
harris.plot_matches(im1,im2,filtered_coords1,filtered_coords2,matches)
show()
if __name__ == '__main__':
im = array(Image.open('D:\Computer vision\School picture\school1.jpg').convert('L'))
im1 = array(Image.open('D:\Computer vision\School picture\school1.jpg').convert('L'))
im2 = array(Image.open('D:\Computer vision\School picture\school11.jpg').convert('L'))
wid=5
harris_points(im)
harris_match(im1,im2,wid)实验结果如下所示:
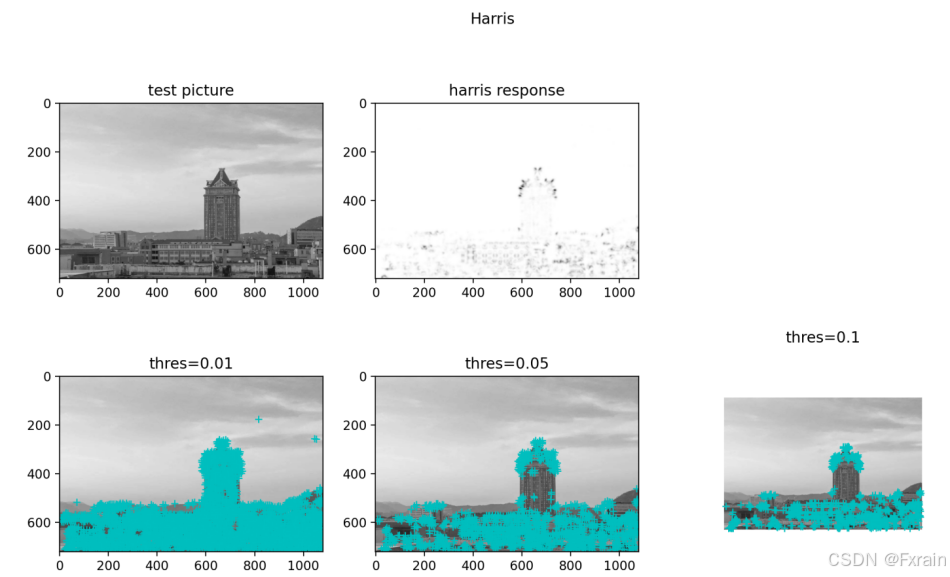
(1)绘制角点
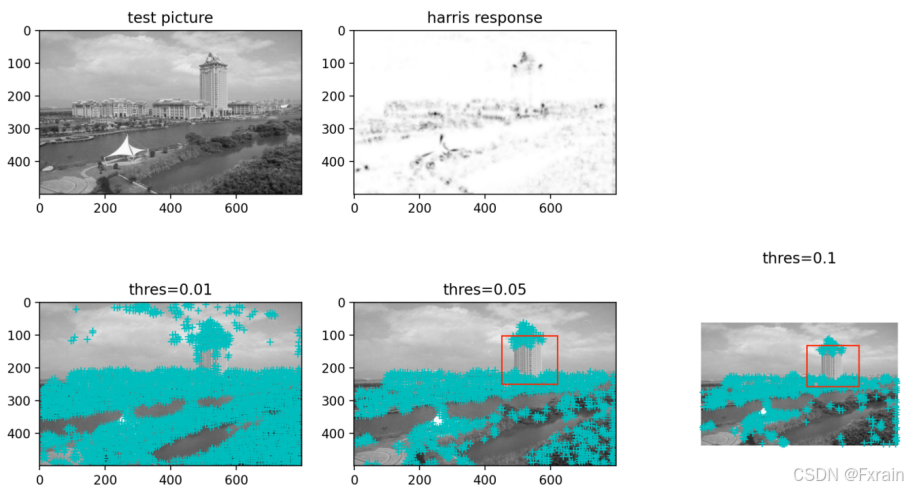
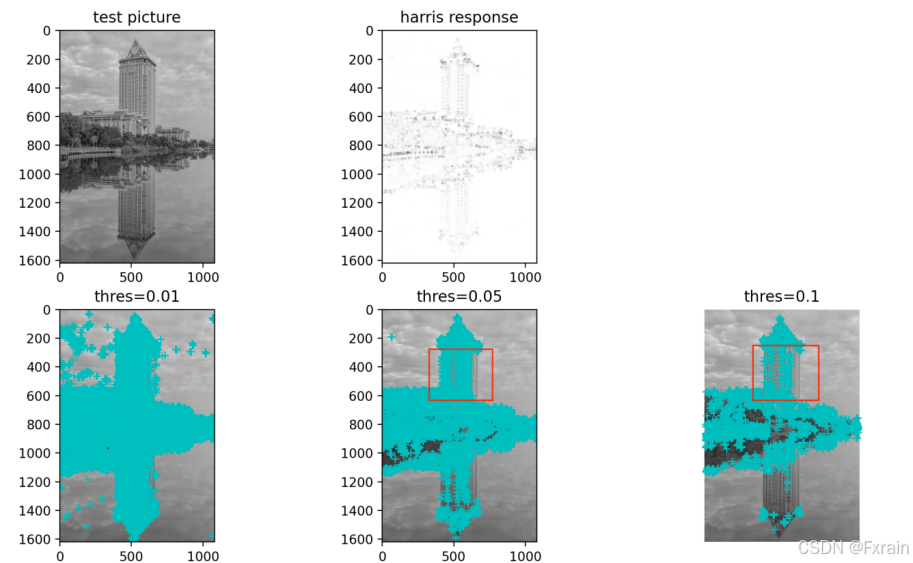
如图1所示,左上角图片为实验使用的灰度图像,第一行第二幅图代表使用Harris角点检测器的Harris响应函数,第二行三幅图分别为使用阈值为0.01检测出的角点图像,使用阈值为0.05检测出的角点图像,使用阈值为0.1检测出的角点图像,通过对比可以发现,使用的阈值越小,检测出的角点数量越多,使用的阈值越大,检测出的角点数量越少。当使用其他测试图像时,运行后的结果如图2、图3所示。对比图2、图3可以看到,当图像放大后,原来能检测到的角点就变成边线了,就检测不到了(对比图2、图3的红色标记框)这是Harris角点检测最大的缺陷,Harris角点检测不具有尺度不变性。
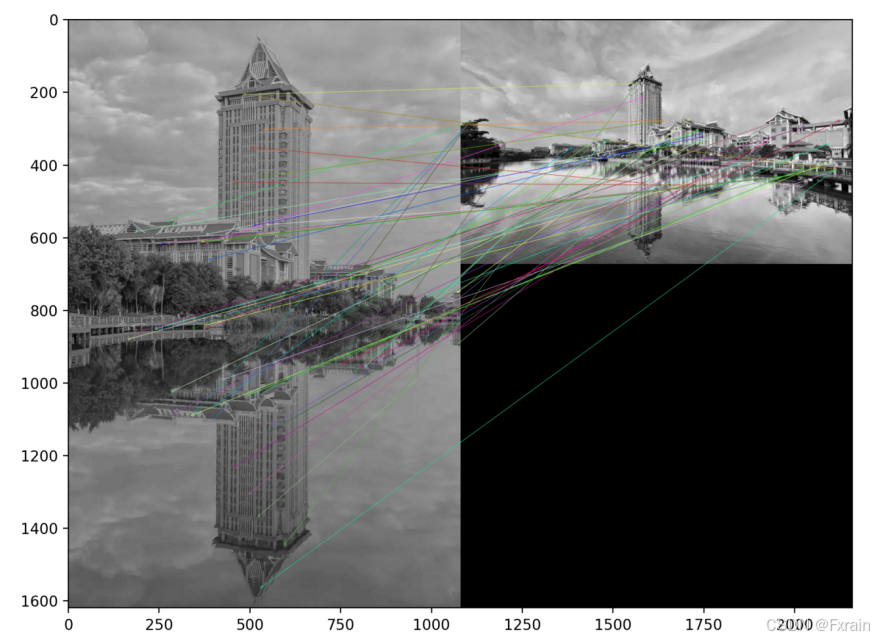
(2)图像的特征匹配
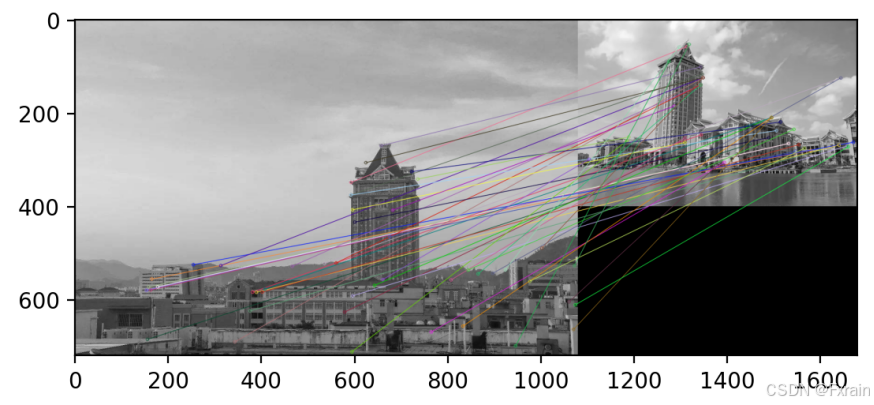
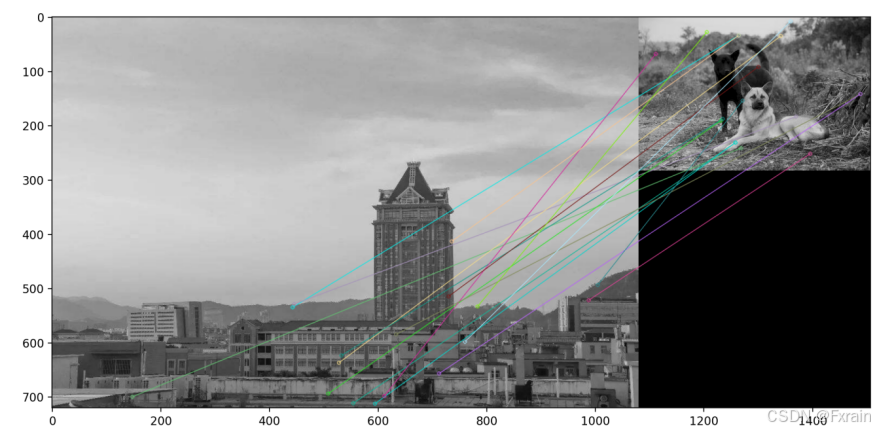
如图4所示,将归一化的互相关矩阵应用于Harris角点周围图像块,来寻找匹配对应点,图中以关键点为中心的邻域的大小,即descriptor描述符的窗口宽度wid=5,对于每一个关键点坐标 coords,都会提取以该点为中心、宽度为 wid 的邻域作为特征描述符。最后,所有的描述符被添加到一个列表 desc 中并返回。当修改窗口宽度wid=8时,结果如图5所示。当使用其他两幅相似的匹配图像时,结果如图6所示。当使用两幅内容不相似的图像时结果如图7所示。




2.2 SIFT算法
以下是sift.py文件
import cv2
import numpy as np
import matplotlib.pyplot as plt
def sift_compute(img1,img2):
sift = cv2.SIFT_create()
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)
FLANN_INDEX_KDTREE = 1
index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
search_params = dict(checks=50)
flann = cv2.FlannBasedMatcher(index_params, search_params)
matches = flann.knnMatch(des1, des2, k=2)
goodMatch = []
for m, n in matches:
if m.distance < 0.75*n.distance:
goodMatch.append(m)
goodMatch = np.expand_dims(goodMatch, 1)
print("匹配点数量级结果: " + str(len(goodMatch)))
#print(goodMatch[:50])
img_out = cv2.drawMatchesKnn(img1, kp1, img2, kp2, goodMatch, None, flags=2)
img_out_rgb = cv2.cvtColor(img_out, cv2.COLOR_BGR2RGB)
plt.figure()
plt.imshow(img_out_rgb)
plt.show()以下是test.py文件
def sift_process(img):
gray= cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
sift = cv2.SIFT_create()
kp,des=sift.detectAndCompute(gray,None)
cv2.drawKeypoints(img,kp,img,flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
plt.figure(figsize=(8,6),dpi=100)
plt.imshow(img[:,:,::-1]),plt.title('sift检测描述子',fontproperties=font)
plt.xticks([]), plt.yticks([])
plt.show()
def sift_match(img1,img2):
sift.sift_compute(img1,img2)
if __name__ == '__main__':
img = cv2.imread('School picture/school1.jpg')
img1 = cv2.imread('D:/Computer vision/School picture/school1.jpg', cv2.IMREAD_GRAYSCALE)
img2 = cv2.imread('D:/Computer vision/School picture/school11.jpg', cv2.IMREAD_GRAYSCALE)
sift_process(img)
sift_match(img1,img2)实验结果如下所示:
(1)绘制描述子
图8为通过opencv使用SIFT算法检测绘制描述子的结果,结果图中显示描述子的方向、尺度信息。当使用其他测试图像时,运行后的结果如图9、图10所示,对比Harris检测,SIFT特征提取具有一定的鲁棒性,即使在图像发生较大变化的情况下,仍然能够找到相似的特征点并生成相应的描述子(对比图2、图3的红色标记框)。



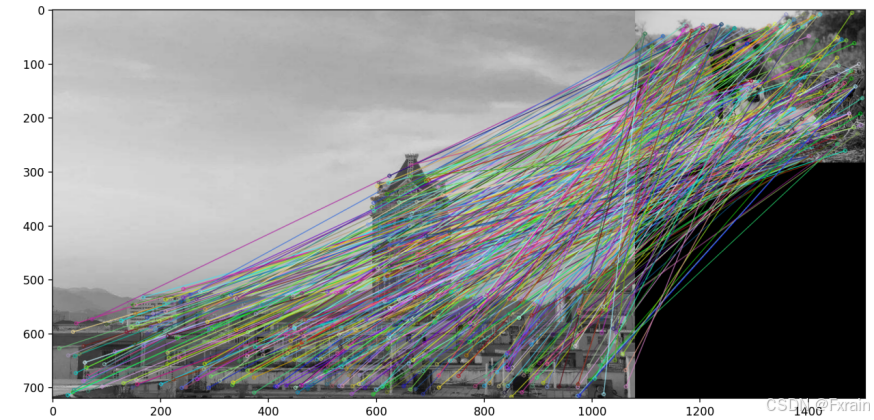
(2)图像的特征匹配
如图11所示,使用OpenCV库中的SIFT算法来检测和计算图像的特征点和描述符,然后使用FLANN匹配器进行特征点匹配。最后将匹配结果绘制在一幅图像上并显示出来。当使用其他两幅相似的匹配图像时,结果如图12所示。当使用两幅不相似的图像时,结果如图13所示。当如果第一个匹配的距离小于第二个匹配距离的0.75倍,即(m.distance < 0.75*n.distance),匹配结果良好,当匹配距离的倍数过大或过小,会导致匹配结果较差(如图14、15)
三、实验小结
Harris角点检测产生的特征点为角点的位置信息,SIDT特征提取为每个特征点生成描述子,包括特征点的方向、尺度等信息。实验中发现,当图像发生缩放、亮度等变换时,Harris角点检测可能会丢失一些角点或产生新的角点,SIFT特征提取具有一定的鲁棒性。
