当前位置：首页 > article >正文

遗传算法与深度学习实战（33）——WGAN详解与实现

article 2025/2/3 1:55:59

遗传算法与深度学习实战（33）——WGAN详解与实现

- 0. 前言
- 1. 训练生成对抗网络的挑战
- 2. GAN 优化问题
- - 2.1 梯度消失
  - 2.2 模式崩溃
- 2.3 无法收敛
- 3 Wasserstein GAN
- - 3.1 Wasserstein 损失
  - 3.2 使用 Wasserstein 损失改进 DCGAN
- 小结
- 系列链接

0. 前言

原始的生成对抗网络 (Generative Adversarial Network, GAN) 在训练过程中面临着模式坍塌和梯度消失等问题，为了解决这些问题，研究人员提出了大量的关键技术以提高GAN模型的整体稳定性，并降低了上述问题出现的可能性。例如 WGAN (Wasserstein GAN) 和 WGAN-GP (Wasserstein GAN-Gradient Penalty) 等，通过对原始生成对抗网络 (Generative Adversarial Network, GAN) 框架进行了细微调整，就能够训练复杂 GAN。在本节中，我们将学习 WGAN 与 WGAN-GP，两者都对原始 GAN 框架进行了细微调整，以改善图像生成过程的稳定性和质量。

1. 训练生成对抗网络的挑战

生成对抗网络 (Generative Adversarial Network, GAN) 需要平衡鉴别器和生成器之间的学习能力，如果任何一个模型超越了另一模型，则整个系统将会失败。由于鉴别器是单独训练的，因此它有机会作为独立的图像识别模型，但在实际应用中，其性能往往不如专门为图像识别训练的模型。
虽然构建和训练 GAN 的目标是能够生成逼真的伪造样本，但同时也能够得到强大的鉴别器，区分给定数据集中的真实样本和伪造样本。鉴别器本质上是一个分类器，可以识别给定数据集中真实样本与伪造样本之间的差异，从而使模型能够重用为所用数据集的简单分类器。例如，如果在面部图像数据集上训练 GAN，则训练后的鉴别器可以用于将图像分类为面部图像或非面部图像。
构建和训练一个能够得到逼真图像的 GAN 是极其困难的，在本节中，我们将探讨训练 GAN 时的问题，并将研究解决这些问题的策略。

2. GAN 优化问题

通常，生成对抗网络 (Generative Adversarial Network, GAN) 训练的主要问题是使生成器和鉴别器有效地并行收敛到一个解。通常，当生成图像中出现各种伪影时，就表明模型遇到了问题，在训练 GAN 时最常见的问题包括：

梯度消失-如果鉴别器擅长识别伪造样本，这通常会减少反馈给生成器的损失量。反过来，减少的损失会降低应用于生成器的训练梯度，并导致梯度消失
模式崩溃-生成器可能会被困在不断生成相同输出的状态中，不同输出间的变化很小。这是因为模型会记住能够骗过鉴别器的单一模式，实质上过拟合了生成的输出
无法收敛-如果生成器在训练过程中改进得太快，会导致鉴别器崩溃，并且基本上在真实或伪造图像之间进行随机猜测

了解这些问题以及出现这些问题的原因对于理解和训练 GAN 非常有用，接下来，我们将复现 GAN 中的这些问题。

2.1 梯度消失

为了复现生成器的梯度消失问题，我们通常只需要调整鉴别器使用的优化器。另外，网络架构也可能导致梯度消失问题，但我们已经采取了批归一化、droput 等措施来解决这一问题。
设置鉴别器优化器，使得鉴别器能更好地或非常好地识别伪造图像和真实图像。因此，随着训练的进行，虽然生成器的损失已经最小化，但输出没有明显改善：

gen_optimizer = Adam(0.0002, 0.5)
disc_optimizer = Adam(.00000001, .5)

训练输出如下图所示，可以看到生成器由于梯度消失而出现的问题。判断GAN是否遇到此问题的两个主要指标是生成器损失和鉴别器对伪造图像的损失，如图所示，鉴别器对伪造品的损失在整个训练过程中保持在一个小范围内不变。对于生成器来说，这会导致随着时间的推移，损失的变化较小，产生梯度消失的现象。

梯度消失

通常，当我们观察到深度学习模型中出现梯度消失时，需要检查模型架构，并寻找可能导致梯度消失的部分。在生成器模型构建时，我们使用了 ReLU 激活函数，可以通过改变生成器的激活函数观察问题是否得到解决：

model.add(Dense(128 * cs * cs, activation="relu", input_dim=latent_dim))
model.add(Reshape((cs, cs, 128)))
model.add(UpSampling2D())
model.add(Conv2D(128, kernel_size=3, padding="same"))
model.add(BatchNormalization(momentum=0.8))
#model.add(Activation("relu"))
model.add(LeakyReLU(alpha=0.2))
model.add(UpSampling2D())
model.add(Conv2D(64, kernel_size=3, padding="same"))
model.add(BatchNormalization(momentum=0.8))
#model.add(Activation("relu"))
model.add(LeakyReLU(alpha=0.2))
model.add(Conv2D(channels, kernel_size=3, padding="same"))
model.add(Activation("tanh"))

修改生成器激活函数后重新运行代码，可以看到模型的改进很小。这是因为问题出在鉴别器上，改变生成器的激活函数并无太大影响。解决 GAN 中梯度消失的常用方法是调整优化器或改变损失计算的方式。

2.2 模式崩溃

当 GAN 的输出几乎完全相同时，则表示发生了模式崩溃，这种情况下，生成器只会学习一种或少量几种能够骗过鉴别器的输出。然后，随着鉴别器的改进，生成器只会在很小范围内变化以得到能够继续欺骗鉴别器的输出。
为了重现 GAN 中的模式崩溃问题，设置鉴别器优化器，使鉴别器以较高速率学习：

gen_optimizer = Adam(0.0002, 0.5)
disc_optimizer = Adam(.002, .9)))

训练 GAN 25 个 epoch 后，结果如下所示，可以看到输出图像的模式崩溃。

模式崩溃

克服模式崩溃的简单方法是选用合适的优化器，也可以通过调整损失函数来解决这一问题。接下来，我们使用一个非常简单的方法来缓解模式崩溃问题，在标签中添加噪声。添加一个布尔型常量 ADD_NOISE，用于控制是否添加噪声：

if ADD_NOISE:
    fake_d = np.random.sample(BATCH_SIZE) * 0.2
    valid_d = np.random.sample(BATCH_SIZE) * 0.2 + 0.8
    valid_g = np.ones((BATCH_SIZE, 1))
else:
    valid_d = np.ones((BATCH_SIZE, 1))
    fake_d = np.zeros((BATCH_SIZE, 1))
    valid_g = np.ones((BATCH_SIZE, 1))

添加噪声后训练 GAN 25 个 epoch 后结果如下所示，可以看到，虽然由于优化器的问题，结果仍然不是很好，但输出图像间已经有所变化。

运行结果

可以看出，只需将噪声添加到标签中，就能够纠正模式崩溃问题。

2.3 无法收敛

无法收敛是 GAN 中的另一潜在问题，可能是模式崩溃、梯度消失或优化不平衡的结果。因此，我们可以相对容易地重现收敛失败的情况。
为了重现收敛失败的情况，设置生成器优化器：

disc_optimizer = RMSprop(.00001)
# convergence
gen_optimizer = RMSprop(.00001)

下图显示了 GAN 生成器收敛失败的情况，尽管鉴别器能够很好的收敛，但生成器损失无法收敛。

无法收敛

纠正收敛问题有一个相对简单的方法是打破生成器和鉴别器训练之间的回合制交替训练，可以通过允许生成器和鉴别器的训练彼此独立地进行循环来实现。
为了支持进行独立的迭代，在训练循环中添加两个内部循环，一个用于训练鉴别器，另一个用于训练生成器。可以使用变量 CRITIC_ITS 控制鉴别器迭代的频率，使用 GEN_ITS 控制生成器迭代的频率：

CRITIC_ITS = 5
GEN_ITS = 10
for e in range(EPOCHS):
    for i in tqdm(range(batches)):
        for _ in range(CRITIC_ITS):
            idx = np.random.randint(0, train_images.shape[0], BATCH_SIZE)
            imgs = train_images[idx]
            noise = np.random.normal(0, 1, (BATCH_SIZE, latent_dim))
            gen_imgs = g.predict(noise)
            d_loss_real = d.train_on_batch(imgs, valid_d)
            d_loss_fake = d.train_on_batch(gen_imgs, fake_d)
            d_loss = 0.5 * np.add(d_loss_real, d_loss_fake)
        for _ in range(GEN_ITS):
            g_loss = gan.train_on_batch(noise, valid_g)

将 CRITIC_ITS 的值设置为 5，将 GEN_ITS 的值设置为10，运行代码，打破生成器和鉴别器之间紧密依赖关系后的 GAN 收敛结果如下所示。

运行结果

3 Wasserstein GAN

WGAN (Wasserstein GAN) 是提高 GAN 训练稳定性方面的一次巨大进步，在经过一些简单改动后 GAN 就能够实现以下两个特点:

与生成器的收敛度和生成样本质量相关的损失度量
优化过程的稳定性得到提高

具体来说，WGAN 针对判别器和生成器提出了一种新的损失函数 (Wasserstein Loss)，用这种损失函数代替二元交叉熵就可以让 GAN 的收敛更加稳定。

3.1 Wasserstein 损失

首先我们来回顾一下二元交叉嫡, 在训练 DCGAN 判别器和生成器时采用以下损失函数：
$-\frac 1 n \sum_{i=1}^n(y_ilog(p_i)+(1-y_i)log(1-p_i))$
为了训练 GAN 的判别器 D，我们根据以下两者计算损失：真实图像的预测 $p_i=D(x_i)$ 与标签 $y_i=1$ 之间的误差，以及生成图像的预测 $p_i=D(G(z_i))$ 与标签 $y_i=0$ 之间的误差。因此，对于 GAN 的判别器来说，损失函数最小化的过程可以表示为:
$\mathop {\min} \limits_{D}-(\mathbb E_{x\sim p_X}[\log D(x)]+\mathbb E_{z\sim p_Z}[\log (1-D(G(z)))])$
为了训练 GAN 的生成器 G，我们根据生成图像的预测 $p_i=D(G(z_i))$ 与标签 $y_i=1$ 的误差计算损失。因此，对于 GAN 的生成器来说，将损失函数最小化的过程可以表示为:
$\mathop {\min}\limits_{G}-(\mathbb E_{z\sim p_Z}[\log D(G(z))])$
接下来，我们比较上述损失函数与 Wasserstein 损失函数。
Wasserstein 损失 (Wasserstein Loss) 是用于 Wasserstein GAN (WGAN) 的一种损失函数。与传统的二元交叉熵损失函数不同，Wasserstein 损失引入了标签 1 和 -1，将判别器的输出从概率值转变为分数 (score)，因此，WGAN 的判别器通常也被称为评论家 (critic)，并要求判别器是 1-Lipschitz 连续函数。
具体来说，Wasserstein 损失使用标签 $y_i=1$ 和 $y_i=-1$ 代替 $y_i=1$ 和 $y_i=0$ ，同时还需要移除判别器最后一层的 Sigmoid激活函数，如此一来预测结果 $p_i$ 就不一定在 $[0, 1]$ 范围内了，它可以是 $[- \infty, \infty]$ 范围内的任何值。Wasserstein 损失的定义如下：
$-\frac 1 n∑_{i=1}^n(y_ip_i)$
在训练 WGAN 的判别器 D 时，我们将计算以下损失：判别器对真实图像的预测 $p_i=D(x_i)$ 与标签 $y_i=1$ 之间的误差，判别器对生成图像的预测 $p_i=D(G(z_i))$ 与标签 $y_i=-1$ 之间的误差。因此，对于 WGAN 判别器，最小化损失函数的过程可以表示为：
$\mathop {\min}\limits_ D - (\mathbb E_{x\sim p_X}[D(x)] - \mathbb E_{z\sim p_Z}[D(G(z))])$
换句话说，WGAN 判别器试图最大化其对真实图像的预测和生成图像的预测之间的差异，且真实图像的得分更高。
而对于 WGAN 生成器 G 的训练，我们根据判别器对生成图像的预测 $p_i=D(G(z_i))$ 与标签 $y_i=1$ 计算损失。因此，对于 WGAN 生成器，最小化损失函数可以表示为：
$\mathop {\min}\limits_ G - (\mathbb E_{z\sim p_Z}[D(G(z))])$
换句话说，WGAN 生成器试图生成被判别器以极高分数判定为真实图像的图像(即，令判别器认为它们是真实的)。

3.2 使用 Wasserstein 损失改进 DCGAN

在本节中，将介绍如何在 GAN 中实现 Wasserstein 距离损失，代码构建在 DCGAN 之上，在其中添加 Wassertein 损失。

(1) 首先，导入所需库和数据集：

from tensorflow.keras.datasets import mnist as data
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.layers import Input, Dense, Activation, Flatten, Reshape, Dropout, ZeroPadding2D
from tensorflow.keras.layers import Conv2D, Conv2DTranspose, UpSampling2D, Convolution2D
from tensorflow.keras.layers import BatchNormalization
from tensorflow.keras.layers import LeakyReLU
from tensorflow.keras.optimizers import Adam, RMSprop

import tensorflow.keras.backend as K

import numpy as np
import matplotlib.pyplot as plt
from livelossplot import PlotLosses
from tqdm import tqdm_notebook

import random
from tqdm.notebook import tqdm as tqdm

(train_images, train_labels), (test_images, test_labels) = data.load_data()

# split dataset
#train_images = train_images.reshape(train_images.shape[0], 28, 28, 1).astype("float32") / 255.0
print(train_images.shape)

# Rescale -1 to 1
train_images = (train_images.astype(np.float32) - 127.5) / 127.5
train_images = np.expand_dims(train_images, axis=3)
print(train_images.shape)

def extract(images, labels, class_):
    idx = labels == class_
    print(idx)
    imgs = images[idx]
    print(imgs.shape)
    return imgs

train_images = extract(train_images, train_labels, 5)

(2) 实例化优化器，将鉴别器模型的名称更改为评论家 critic，这是因为评论家预测真实性或虚假性的量度，而不是真实或虚假的概率，生成器和评论家使用相同的优化器。我们之所以能够这样做，也是因为各项度量之间的差异被归一化了：

latent_dim = 100

gen_optimizer = RMSprop(lr=0.00005)
critic_optimizer = RMSprop(lr=0.00005)

(3) 使用 wasserstein_loss() 函数计算 Wasserstein 损失。将真实输入的平均值与预测值相乘，输出两个分布之间的 Wasserstein 距离：

def wasserstein_loss(y_true, y_pred):
return K.mean(y_true * y_pred)

cs = int(train_images.shape[1] / 4)
print(train_images.shape)
channels = train_images.shape[3]
img_shape = (train_images.shape[1], train_images.shape[2], channels)

然后，在评论家模型编译时使用 wasserstein_loss 函数。

(4) 更新评论家训练代码。Wasserstein 损失引入了爆炸梯度的可能性，为了解决这一问题，添加权重裁剪步骤，对于评论家的每个训练迭代，确保将每个模型权重裁剪到 clip_value 超参数内。这种权重剪切消除了可能出现的爆炸梯度，并降低了收敛模型空间：

def build_generator():
    model = Sequential()

    model.add(Dense(128 * cs * cs, activation="relu", input_dim=latent_dim))
    model.add(Reshape((cs, cs, 128)))
    model.add(UpSampling2D())
    model.add(Conv2D(128, kernel_size=3, padding="same"))
    model.add(BatchNormalization(momentum=0.8))
    model.add(Activation("relu"))
    model.add(UpSampling2D())
    model.add(Conv2D(64, kernel_size=3, padding="same"))
    model.add(BatchNormalization(momentum=0.8))
    model.add(Activation("relu"))
    model.add(Conv2D(channels, kernel_size=3, padding="same"))
    model.add(Activation("tanh"))

    model.summary()

    noise = Input(shape=(latent_dim,))
    img = model(noise)

    return Model(noise, img)
g = build_generator()

def build_critic():
    model = Sequential()
    model.add(Conv2D(32, kernel_size=3, strides=2, input_shape=img_shape, padding="same"))
    model.add(LeakyReLU(alpha=0.2))
    model.add(Dropout(0.25))
    model.add(Conv2D(64, kernel_size=3, strides=2, padding="same"))
    model.add(ZeroPadding2D(padding=((0,1),(0,1))))
    model.add(BatchNormalization(momentum=0.8))
    model.add(LeakyReLU(alpha=0.2))
    model.add(Dropout(0.25))
    model.add(Conv2D(128, kernel_size=3, strides=2, padding="same"))
    model.add(BatchNormalization(momentum=0.8))
    model.add(LeakyReLU(alpha=0.2))
    model.add(Dropout(0.25))
    model.add(Conv2D(256, kernel_size=3, strides=1, padding="same"))
    model.add(BatchNormalization(momentum=0.8))
    model.add(LeakyReLU(alpha=0.2))
    model.add(Dropout(0.25))
    model.add(Flatten())
    model.add(Dense(1))

    model.summary()

    img = Input(shape=img_shape)
    validity = model(img)

    return Model(img, validity)

critic = build_critic()
critic.compile(loss=wasserstein_loss,
            optimizer=critic_optimizer,
            metrics=['accuracy'])

(5) 在 MNIST 手写数字数据集的单个类别上训练 80 个 epoch，结果如下图所示。还可以删除对 extract() 函数的调用，以查看模型在数据集的所有类别中的表现：

z = Input(shape=(latent_dim,))
img = g(z)

# For the combined model we will only train the generator
critic.trainable = False

# The discriminator takes generated images as input and determines validity
valid = critic(img)

# The combined model  (stacked generator and discriminator)
# Trains the generator to fool the discriminator
gan = Model(z, valid)
gan.compile(loss=wasserstein_loss, optimizer=gen_optimizer)

def plot_generated(n_ex=10, dim=(1, 10), figsize=(12, 2)):
    noise = np.random.normal(0, 1, size=(n_ex, latent_dim))
    generated_images = g.predict(noise)
    generated_images = generated_images.reshape(n_ex, img_shape[0], img_shape[1])

    plt.figure(figsize=figsize)
    for i in range(generated_images.shape[0]):
        plt.subplot(dim[0], dim[1], i+1)
        plt.imshow((1-generated_images[i])*255, interpolation='nearest', cmap='gray_r')
        plt.axis('off')
    plt.tight_layout()
plt.show()

EPOCHS = 75 #@param {type:"slider", min:5, max:100, step:1}
BATCH_SIZE = 256 #@param {type:"slider", min:64, max:256, step:2}
CRITIC_ITS = 5 #@param {type:"slider", min:1, max:10, step:1}

clip_value = .01

groups = { "Critic" : {"Real", "Fake"}, "Generator":{"Gen"}}
plotlosses = PlotLosses(groups=groups)

plt_frq = 1
batches = int(train_images.shape[0] / BATCH_SIZE)

# Adversarial ground truths
valid = -np.ones((BATCH_SIZE, 1))
fake = np.ones((BATCH_SIZE, 1))

for e in range(EPOCHS):
    for i in tqdm(range(batches)):
        for _ in range(CRITIC_ITS):
            #  Train Critic
            # Select a random half of images
            idx = np.random.randint(0, train_images.shape[0], BATCH_SIZE)
            imgs = train_images[idx]  

            # Sample noise and generate a batch of new images
            noise = np.random.normal(0, 1, (BATCH_SIZE, latent_dim))
            gen_imgs = g.predict(noise)

            # Train the critic (real classified as ones and generated as zeros)
            c_loss_real = critic.train_on_batch(imgs, valid)
            c_loss_fake = critic.train_on_batch(gen_imgs, fake)
            c_loss = 0.5 * np.add(c_loss_real, c_loss_fake)  
            
            #clip critic weights
            for l in critic.layers:
                weights = l.get_weights()
                weights = [np.clip(w, -clip_value, clip_value) for w in weights]
                l.set_weights(weights) 

            #  Train Generator
            g_loss = gan.train_on_batch(noise, valid)  

    loss = dict(Real = c_loss[0], Fake = c_loss[1], Gen = g_loss)  
    plotlosses.update(loss)
    plotlosses.send()
    plot_generated()

运行结果

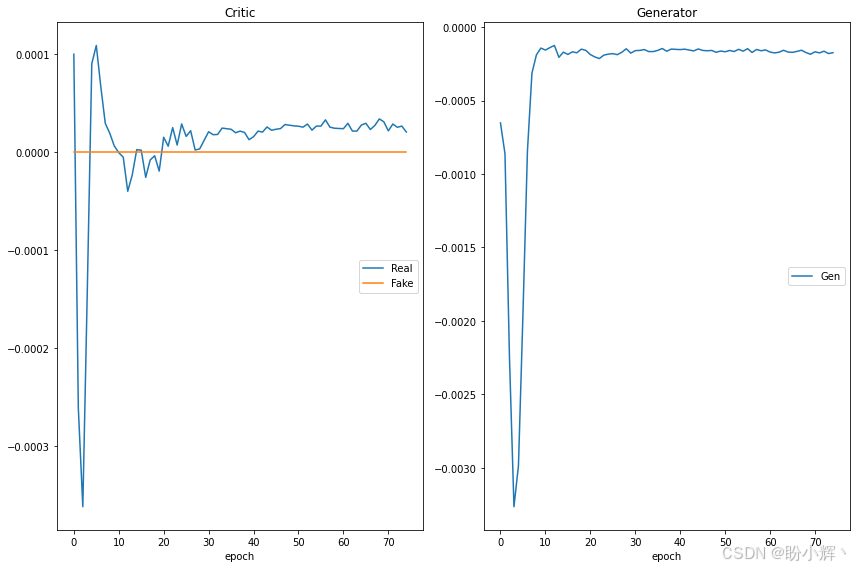
将 Wasserstein 损失引入 DCGAN 消除了标准 GAN 的几个问题，使我们更容易构建最佳 GAN。

小结

WGAN 是 GAN 的一种变体，通过使用 Wasserstein 距离来衡量生成样本与真实样本之间的差异。在本节中，我们学习了如何使用 Wasserstein 损失函数以解决经典 GAN 训练过程中的模式坍塌和梯度消失等问题，使得 GAN 的训练过程更加稳定和可靠。

系列链接

遗传算法与深度学习实战（1）——进化深度学习
遗传算法与深度学习实战（2）——生命模拟及其应用
遗传算法与深度学习实战（3）——生命模拟与进化论
遗传算法与深度学习实战（4）——遗传算法（Genetic Algorithm）详解与实现
遗传算法与深度学习实战（5）——遗传算法中常用遗传算子
遗传算法与深度学习实战（6）——遗传算法框架DEAP
遗传算法与深度学习实战（7）——DEAP框架初体验
遗传算法与深度学习实战（8）——使用遗传算法解决N皇后问题
遗传算法与深度学习实战（9）——使用遗传算法解决旅行商问题
遗传算法与深度学习实战（10）——使用遗传算法重建图像
遗传算法与深度学习实战（11）——遗传编程详解与实现
遗传算法与深度学习实战（12）——粒子群优化详解与实现
遗传算法与深度学习实战（13）——协同进化详解与实现
遗传算法与深度学习实战（14）——进化策略详解与实现
遗传算法与深度学习实战（15）——差分进化详解与实现
遗传算法与深度学习实战（16）——神经网络超参数优化
遗传算法与深度学习实战（17）——使用随机搜索自动超参数优化
遗传算法与深度学习实战（18）——使用网格搜索自动超参数优化
遗传算法与深度学习实战（19）——使用粒子群优化自动超参数优化
遗传算法与深度学习实战（20）——使用进化策略自动超参数优化
遗传算法与深度学习实战（21）——使用差分搜索自动超参数优化
遗传算法与深度学习实战（22）——使用Numpy构建神经网络
遗传算法与深度学习实战（23）——利用遗传算法优化深度学习模型
遗传算法与深度学习实战（24）——在Keras中应用神经进化优化
遗传算法与深度学习实战（25）——使用Keras构建卷积神经网络
遗传算法与深度学习实战（26）——编码卷积神经网络架构
遗传算法与深度学习实战（27）——进化卷积神经网络
遗传算法与深度学习实战（28）——卷积自编码器详解与实现
遗传算法与深度学习实战（29）——编码卷积自编码器架构
遗传算法与深度学习实战（30）——使用遗传算法优化自编码器模型
遗传算法与深度学习实战（31）——变分自编码器详解与实现
遗传算法与深度学习实战（32）——生成对抗网络详解与实现