Deep Crossing：深度交叉网络在推荐系统中的应用

实验和完整代码

完整代码实现和jupyter运行：https://github.com/Myolive-Lin/RecSys--deep-learning-recommendation-system/tree/main

引言

在机器学习和深度学习领域，特征工程一直是一个关键步骤，尤其是对于大规模的推荐系统和广告点击率预测任务。传统的特征工程通常依赖于手动设计的组合特征，这些特征虽然有效，但在大规模数据场景下，其开发和维护成本极高。Deep Crossing 是一种新型的深度学习模型，能够自动学习特征组合，无需手动设计组合特征，从而在大规模数据上实现高效建模。

背景知识

Deep Crossing 是由微软研究院提出的一种深度神经网络模型，专门用于处理大规模稀疏特征数据。该模型的核心思想是通过嵌入层（Embedding Layer）、残差单元（Residual Units）和评分层（Scoring Layer）自动学习特征之间的复杂交互关系。Deep Crossing 的主要贡献在于它能够自动发现重要的特征组合，而无需依赖于手动设计的组合特征。

1. 模型结构

Deep Crossing 的网络结构主要包括以下几个部分：

1. Embedding 层
   • 将稀疏的类别特征嵌入到低维的稠密向量中。每个类别特征都有一个对应的嵌入矩阵，嵌入矩阵的大小为 (类别数, 嵌入维度)。
   • 例如，对于用户 ID 和项目 ID 等类别特征，可以将其嵌入到一个低维的稠密向量中，以便神经网络能够更好地处理。
2. 残差单元（Residual Units）
   • 残差单元是 Deep Crossing 的核心部分，用于学习特征之间的复杂交互关系。每个残差单元包含两个全连接层（nn.Linear），中间通过非线性激活函数（ReLU）和批量归一化（BatchNorm）进行处理。
   • 残差单元的输出通过残差连接（Residual Connection）与输入相加，从而保留了输入的特征信息，避免了梯度消失问题。
3. 评分层（Scoring Layer）
   • 评分层是一个全连接层，用于将经过残差单元处理后的特征向量映射到最终的预测值。输出层通常使用 Sigmoid 函数将输出值映射到 [0, 1] 范围内，表示预测的概率。

模型结构如下：

其中Feature #1 和 Features #n都是分类型数据，Feature #2是数值型数据

残差模块结构如下：

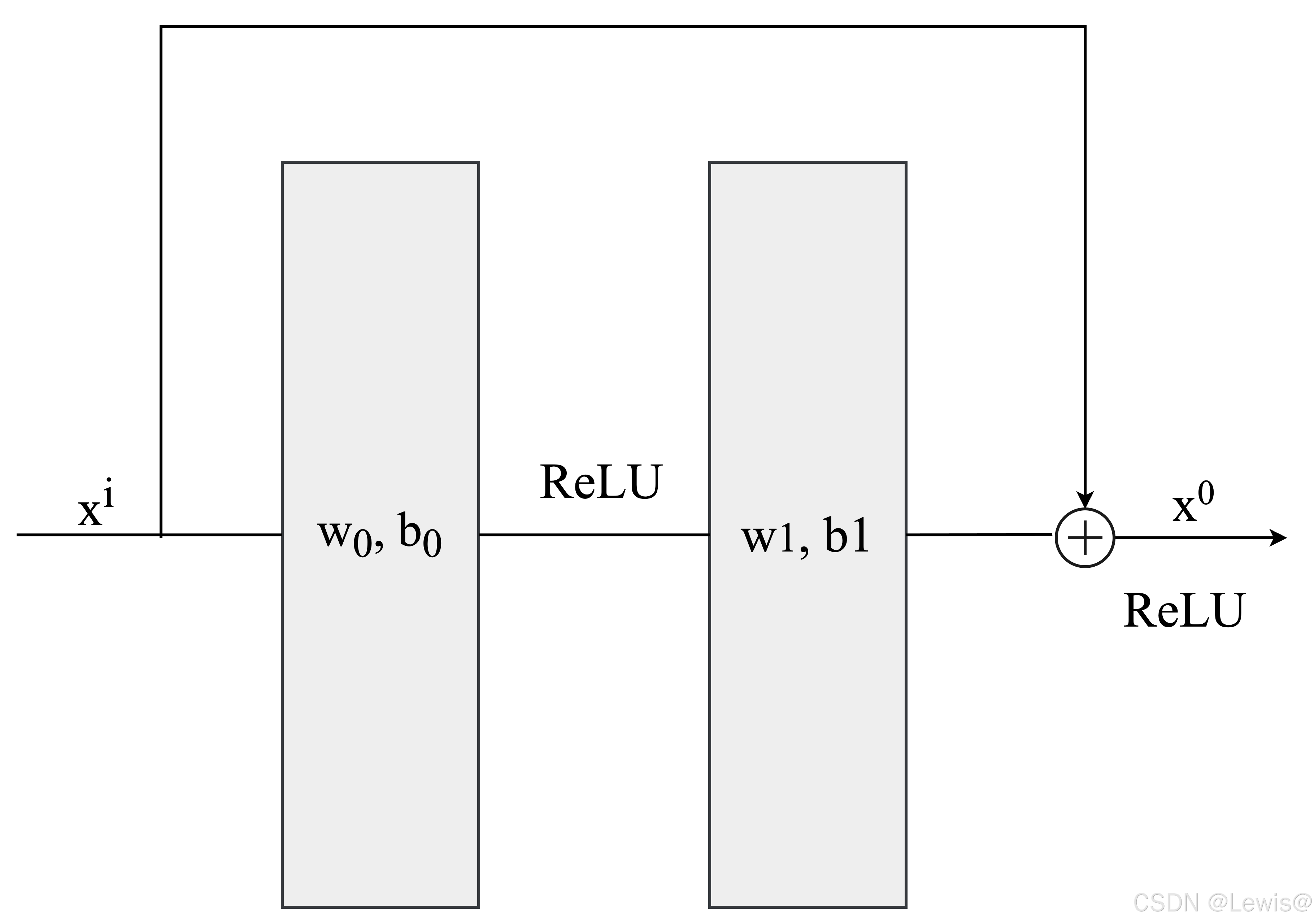
随着网络的加深，梯度在反向传播过程中可能会逐渐衰减（梯度消失）或指数级增长（梯度爆炸）。残差连接（Residual Connection） 通过 恒等映射（Identity Mapping），使梯度可以直接沿着跳跃连接传播，从而减轻梯度消失或爆炸的问题。这对于深度神经网络（DNN）而言尤为重要。

数学上，假设残差模块的输入为 $\mathbf{x}$，非线性变换为 $F(\mathbf{x})$，则输出为：

$$y=F(x)+x$$

这样，在反向传播时，梯度可以通过 $F(\mathbf{x})$ 传播，也可以通过恒等映射直接传播：

$$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}=\frac{\partial F(\mathbf{x})}{\partial \mathbf{x}}+1$$

这保证了梯度不会因层数加深而过度衰减。

此外，从模型的表达能力来看，由于残差模块能够直接建模

$$F(x)=H(x)-x$$

模型学习的是输入和输出之间的残差，而不是直接拟合输出$H(X)$，使得模型更容易优化，也能学习到更复杂的特征交互关系。

2. 模型理论框架

2.1 整体架构

Deep Crossing采用经典的Embedding+MLP范式，其数学表达为：

$$\hat{y}=\sigma (W^{(L)}\cdot h^{(L-1)}+b^{(L)})$$

其中$h^{(l)}$表示第$l$层隐藏状态，包含以下核心组件：

1. 特征嵌入层

​ 对类别型特征$c_i\in {\mathbb{R}}^{d_i}$进行降维：

$$e_i=E_i^T{c}_i,E_i\in {\mathbb{R}}^{d_i\times k}$$

​ 数值型特征直接标准化处理：

$$v_j=\frac{x_j-{\mu }_j}{{\sigma }_j}$$

2. 特征堆叠层

​ 将各特征向量拼接：

$$h^{(0)}=[e_1;e_2;...;e_m;v_1;v_2;...;v_n]$$

3. 残差层

采用改进的残差单元（受ResNet启发）：

$$h^{(l)}=f(W_2^{(l)}\cdot \text{ReLU}(W_1^{(l)}{h}^{(l-1)}+b_1^{(l)})+b_2^{(l)})+h^{(l-1)}$$
其中f为激活函数，实验表明ReLU效果最优。

4. 评分层

最终预测层实现为：

$$p=\text{sigmoid}(W^{(L)}{h}^{(L-1)}+b^{(L)})$$

3. 代码实现

残差模块

#残差网络块
class ResidualUnit(nn.Module):
    def __init__(self, input_dim, hidden_dim, dropout_rate):
        super(ResidualUnit, self).__init__()
        self.layers = nn.Sequential(
            nn.Linear(input_dim, hidden_dim),
            nn.BatchNorm1d(hidden_dim),
            nn.ReLU(),
            nn.Dropout(dropout_rate),
            nn.Linear(hidden_dim, input_dim),
            nn.BatchNorm1d(input_dim),
            nn.Dropout(dropout_rate)
        )
        self.relu = nn.ReLU()
    
    def forward(self, x):
        residual = self.layers(x)
        return self.relu(x + residual)
    

Deep Crossing模块

class DeepCrossing(nn.Module):
    def __init__(self, cat_sizes, num_sizes, config):
        super(DeepCrossing, self).__init__()

        #Embedding层
        self.embeddings = nn.ModuleList([
            nn.Embedding(size, config.embedding_dim ) for size in cat_sizes #生成对应 Embedding层    
        ])

        #计算总特征维度
        total_dim = len(cat_sizes) * config.embedding_dim + num_sizes

        #多层Residual units
        self.res_uint = nn.Sequential()
        for _ in range(config.num_residual_units):
            self.res_uint.append(
                ResidualUnit(total_dim, config.hidden_dim, config.dropout_rate)
            )

        #scoring层
        self.fc = nn.Linear(total_dim,1)

    def forward(self, x_cat, x_num):
        #处理类别特征,注意x_cat 每一列都是一个类别特征,采用类似Ordinal Encoder
        embeddings = []
        for i in range(len(self.embeddings)):
            embeddings.append(self.embeddings[i](x_cat[:,i]))
        
        x = torch.cat(embeddings, dim = 1) #拼接起来

        #拼接数值特征
        x = torch.cat([x,x_num], dim = 1)

        #残差单元
        x = self.res_uint(x)

        #输出层
        return torch.sigmoid(self.fc(x)).squeeze()
        
        

4. 实验

由于没有合适的数据，使用sklearn中make_classification方法生成的数据进行实验如下：

实验结果表明，Deep Crossing 模型在训练和测试集上都表现良好，损失逐渐减小，AUC 分数逐渐提高，且训练和测试结果接近，说明模型能够有效地学习特征之间的交互关系，并具有良好的泛化能力。这些结果验证了 Deep Crossing 模型在处理大规模稀疏数据和自动特征学习方面的优势。

总结

Deep Crossing 通过 Residual Network 深度建模特征交互，避免了手工特征工程的复杂性，并在 CTR 预估等任务中表现优异。相比于传统神经网络，残差结构的加入有效缓解了梯度消失问题，使得深度学习在推荐系统领域取得更大突破。

Reference

[1]. Y. Shan, T. R. Hoens, J. Jiao, H. Wang, D. Yu, and J. C. Mao, “Deep Crossing: Web-Scale Modeling without Manually Crafted Combinatorial Features,” in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2016, pp. 255-262.