图的基本术语——非八股文

        我之前只看到了数据结构与算法的冰山一角，感觉这些术语只会让知识越来越难理解，现在来看，他们完美抽象一些概念和知识，非常重要。

        本篇概念肯定总结不全，只有遇到的会写上，持续更新，之前文章已经提过的如并查集、最短路径、邻接表等不再重复，这里为补充。

        图形结构中的元素之间存在多对多的联系。

        图形结构中，每一个元素前驱结点可以有多个，后继结点也可以有多个。    

         首先我们肯定都知道图可以分为有向图和无向图，它们各自有一些独属于自己的术语和共同的术语，下面这个思维导图帮大家理清一些概念：  

共同术语 

我们先从共同的概念说起 ：

• 完全图：针对有向图和无向图，即每两个顶点都有一条边（有向图至少  条边，无向图至少条边），如图所示。

• 稀疏图与稠密图 ：根据概念来说，有很少条边或弧（如  ，其中e为边的数目，n为顶点的个数）。需要注意的的是，因为这两个概念常用于选择邻接矩阵或邻接表，具体选用要与算法结合。
• 权和网：权和网可以理解为带权图，在绝大数应用中，每条边应该是带有权重的，权可以表示从一个顶点到另一个顶点的距离、时间或代价等含义。
• 邻接点：无向图中邻接点是没有方向的，或者称为对称的，假若顶点v 和顶点w 之间存在一条边， 则称顶点v 和w 互为邻接点。在有向图中，邻接点是有方向的，如果存在从顶点到顶点的有向边，那么我们说顶点是顶点的出边邻接点，顶点是顶点的入边邻接点。

无向图

• 连通：两个顶点有路径。
• 连通图：任意两个顶点有路径，但不一定都有边。
• 连通分量：指在无向图中的极大连通子图，如图中的无向非连通图有两个连通分量。

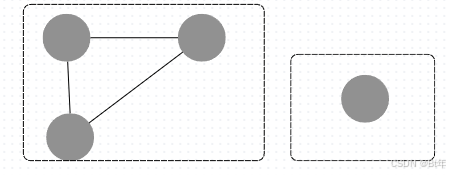
• 度：顶点v的度是指和v相关联的边的数目；如图中，顶点v的度为3。

有向图

• 强连通图：任意两个顶点有路径，但不一定都有边。（注意并不一定两个顶点和有两条边，只要可以形成环就行。）完全有向图肯定就是强连通图。
• 强连通分量：有向图中的极大强连通子图称作有向图的强连通分量，如图所示的有向非强连通图有两个强连通分量。

• 出度和入度：对于有向图，顶点v的度被分为出度和入度，入度是以顶点v为头的的弧数目（箭头指向v），出度就是以顶点v为尾的的弧数目。顶点v的入度为1，出度为2。 

压缩存储

        压缩存储是指在不丢失数据信息的前提下，对数据进行重新编码或组织，以减少数据所占用的存储空间的方法。通过特定的算法和数据结构，将原始数据转换为一种更紧凑的表示形式，在需要使用数据时再进行解压缩还原。

        这里主要介绍矩阵的压缩存储。

        对称矩阵

        即，首先我们先回顾一个等差数列的公式：。

根据这个公式，我们就可以把一个n维矩阵，用一个一维数组进行存储了。无向图的邻接矩阵就是对称矩阵可用一维数组压缩储存。 

        可以按行主序即下三角存储；或者按列主序即上三角存储。如果我们要找矩阵中位置第i行第j列的元素,还是利用上面等差数列公式按行存储和列存储即可搞定。

        三角矩阵

        三角矩阵即只有矩阵的一个三角的数字有意义，对称矩阵就可以理解为三角矩阵，所以三角矩阵的压缩储存与对角矩阵基本一样。

        对角矩阵

        就是只在对角线上存在的元素有意义。 一般分两种方式存储：行序存储和对角线。

        可以将主对角线元素存储在一个一维数组中，通过数组下标与矩阵主对角线元素的对应关系来实现对矩阵元素的访问和操作。例如，对于对角矩阵的主对角线元素，可以存储在一维数组中，。

        其它

        另外稀疏矩阵的压缩存储可以用一个三元组表来表示稀疏矩阵中的非0元素。

        稀疏矩阵是指矩阵中绝大多数元素为 0，只有少数非 0 元素的矩阵。为了节省存储空间和提高运算效率，通常采用压缩存储的方式来存储稀疏矩阵，其中一种常见的方法就是用三元组表来表示稀疏矩阵中的非 0 元素。

        三元组表中的每个三元组通常表示为（行标，列标，值），分别记录了稀疏矩阵中每个非 0 元素所在的行、列位置以及该元素的值。通过这种方式，可以只存储稀疏矩阵中的非 0 元素，而不必像常规的二维数组存储方式那样为大量的 0 元素分配存储空间，从而达到压缩存储的目的。例如，对于一个稀疏矩阵：

        可以用三元组表表示为：{(1, 1, 1), (2, 3, 3), (4, 2, 4)}

        除了三元组表，压缩存储稀疏矩阵还可以使用十字链表等其他方法。

参考文献

稠密图与稀疏图判别 - 焓青 - 博客园

【数据结构】图的基本概念—无/有向图、权和网、完全图、路径与回路-阿里云开发者社区