机器学习笔记:层次聚类
1 原理
1.1 主体思路
- 通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。
- 在聚类树中,不同类别的原始数据点是树的最低层,树的顶层是一个聚类的根节点。
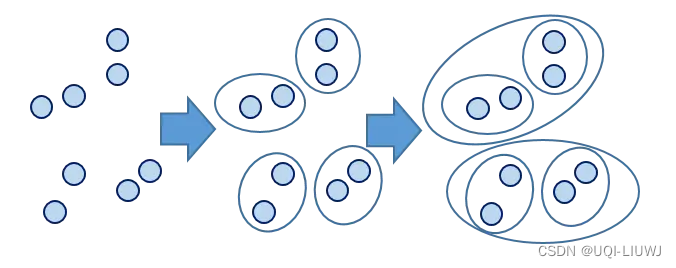
- 创建聚类树有自下而上合并(凝聚层次分类,agglomerative)和自上而下分裂(分裂层次分类,divisive)两种方法
- 自下而上:先让所有点分别成为一个单独的簇,然后通过相似性不断组合,直到最后只有一个簇为止
- 自上而下:从单个集群开始逐步分裂,直到无法分裂(无法继续分裂即每个点都是一个簇)
- 自下而上:先让所有点分别成为一个单独的簇,然后通过相似性不断组合,直到最后只有一个簇为止
1.2 两个簇之间的距离
1.2.1 single linkage
- 两个簇中距离最近的两个数据点间的距离作为这两个簇的距离
- 问题:两个不相似的簇,可能因为其中的两个极端值很近,故而合并到了一块
1.2.2 complete linkage
- 两个簇中距离最远的两个数据点间的距离作为这两个簇的距离
- 问题:两个相似的簇,可能因为其中的两个极端值很远,故而无法合并到了一块
1.2.3 Average linkage
- 计算两个簇中的每个数据点与其他所有数据点的距离。
- 将所有距离的均值作为两个簇间的距离。
- 这种方法计算量比较大,但结果比前两种方法更合理。
- 比如簇(A,F)和簇(B,C)之间的距离可以计算为:

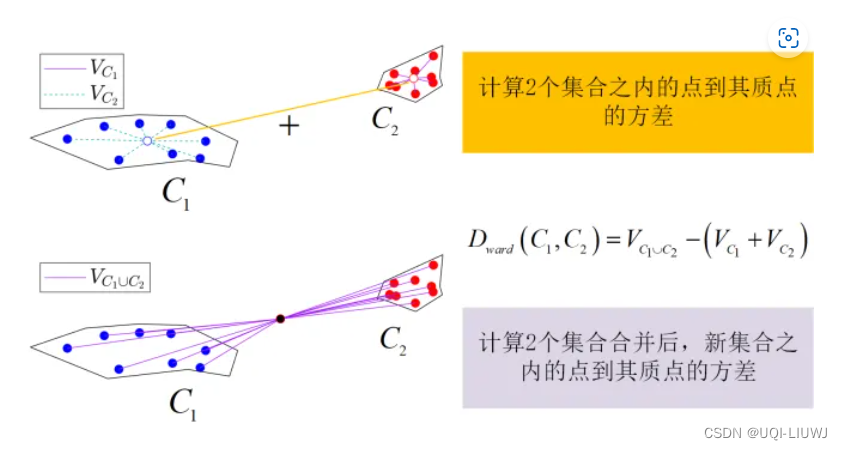
1.2.4 Ward
2 举例
2.1 问题描述
- 一位老师想要将学生分成不同的组。
- 现在有每个学生在作业中的分数,想根据这些分数将他们分成几组。
- 关于拥有多少组,这里没有固定的目标(K-means需要事先提供K,层次聚类则不需要)
| Student_ID | Marks |
| 1 | 10 |
| 2 | 7 |
| 3 | 28 |
| 4 | 20 |
| 5 | 35 |
2.2 解决方法(自下而上的层次聚类)
2.2.1 创建临近矩阵
这里的距离就是两个学生成绩的差
| ID | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 3 | 18 | 10 | 25 |
| 2 | 3 | 0 | 21 | 13 | 28 |
| 3 | 18 | 21 | 0 | 8 | 7 |
| 4 | 10 | 13 | 8 | 0 | 15 |
| 5 | 25 | 28 | 7 | 15 | 0 |
2.2.2 合并聚类
这里我们假设使用single linkage
- 首先,每个学生单独成簇
- 【1】【2】【3】【4】【5】
- 然后找临近矩阵中最小的非零距离,合并距离最小的两个簇
- 此时最小的距离是【1】和【2】
- ——>【1,2】【3】【4】【5】
- 然后更新临近矩阵
-
ID (1,2) 3 4 5 (1,2) 0 18 10 25 3 18 0 8 7 4 10 8 0 15 5 25 7 15 0
-
-
接下来最近的是【3】和【5】
-
合并之【1,2】【3,5】【4】
-
-
再计算临近矩阵
-
ID (1,2) (3,5) 4 (1,2) 0 18 10 (3,5) 18 0 8 4 10 8 0
-
-
然后聚类【3,5】和【4】
-
ID (1,2) (3,4,5) (1,2) 0 10 (3,4,5) 10 0
-
-
最后把【1,2】和【3,4,5】合并,层次聚类结束
2.2.3 如何聚类

- 1,我需要k个类,那么我们就从下而上不断合并,直至还剩k个类
参考内容:
一文读懂层次聚类(Python代码) - 知乎 (zhihu.com)
机器学习--聚类系列--层次聚类 - 理想几岁 - 博客园 (cnblogs.com)