Chapter8.3:控制系统校正的根轨迹法
该系列博客主要讲述Matlab软件在自动控制方面的应用,如无自动控制理论基础,请先学习自动控制系列博文,该系列博客不再详细讲解自动控制理论知识。
自动控制理论基础相关链接:https://blog.csdn.net/qq_39032096/category_10287468.html?spm=1001.2014.3001.5482
博客参考书籍:《MATLAB/Simulink与控制系统仿真》。
3.控制系统校正的根轨迹法
3.1 概述
- 根轨迹法是一种图解法,描述了系统某一参数从零变化到无穷大时,其闭环极点位置的变化;
- 通过引入适当的校正装置来改变原来系统的根轨迹,以获得期望的系统性能;
- 引入校正装置即在系统中增加零极点,通过零极点的变化改变根轨迹的形状;
- 用根轨迹法进行校正的基础,是通过在系统开环传递函数中增加零极点来改变根轨迹的形状,从而使系统根轨迹在 s s s平面上通过希望的闭环极点;
- 根轨迹法校正的特征是基于闭环系统具有一对主导闭环极点,零点和附加的极点会影响响应特性;
- 应用根轨迹进行校正,实质上是通过采用校正装置改变根轨迹,从而将一对主导闭环极点配置到期望的位置上;
- 在开环传递函数中增加极点,可以使根轨迹向右方移动,从而降低系统的相对稳定性,增大系统调节时间;
- 在开环传递函数中增加零点,可以使根轨迹向左方移动,从而提高系统的相对稳定性,减小系统调节时间;
- 当系统性能指标是以最大超调量、上升时间、调节时间、阻尼比,及希望的闭环阻尼比、闭环极点无阻尼频率等表示时,采用根轨迹法进行校正较为方便;
- 采用根轨迹法确定串联校正参数的条件是:
- 已确定采用串联校正方案;
- 给定时域指标: σ p 、 t s 、 e s s ( ∞ ) \sigma_p、t_s、e_{ss}(\infty) σp、ts、ess(∞);
3.2 基于根轨迹法的超前校正
用根轨迹法设计超前校正装置步骤:
-
先假定系统的控制性能由靠虚轴最近的一对闭环共轭极点 s d s_d sd主导;
-
应用二阶系统参量 ζ \zeta ζ和 ω n \omega_n ωn与时域指标之间的关系,按给定的 σ p \sigma_p σp和 t s t_s ts确定闭环主导极点的位置;
-
绘制原系统根轨迹,如果根轨迹不能通过希望的闭环主导极点,则表明仅调整增益不能满足给定要求,需要增加校正装置;如果原系统根轨迹位于期望极点的右侧,则应加入超前校正装置;
-
计算超前校正装置应提供的超前相角;
-
按下式计算校正装置零极点位置:
φ c = ± ( 2 k + 1 ) π − ∠ G 0 ( s d ) \varphi_c=±(2k+1)\pi-\angle{G_0(s_d)} φc=±(2k+1)π−∠G0(sd) -
由幅值条件确定校正后系统增益;
-
校验系统的性能指标,如果系统不能满足要求指标,适当调整零极点位置;如果需要大的静态误差系数,则应采用其他方案;
3.3 基于根轨迹法的滞后校正
用根轨迹法设计滞后校正装置步骤:
- 绘制出未校正系统的根轨迹;
- 根据要求的瞬态响应指标,确定希望的闭环主导极点,根据根轨迹的幅值条件,计算与主导极点对应的开环增益;
- 按给定的性能指标中关于稳态误差的要求,计算应增大的误差系数值;
- 由应增大的误差系数值确定校正装置 β \beta β值,通常 β \beta β取值不超过 10 10 10;
- 确定滞后校正装置的零极点,原则是使零极点靠近坐标原点,且两者相距 β \beta β倍;
- 绘制校正后系统的根轨迹,并求出希望的主导极点;
- 由希望的闭环极点,根据幅值条件,适当调整放大器的增益;
- 校验校正后系统各项性能指标,如不满足要求,则适当调整校正装置零极点位置;
3.4 基于根轨迹法的超前滞后校正
用根轨迹法设计超前滞后校正装置步骤:
-
根据要求的性能指标,确定希望的主导极点 s d s_d sd位置;
-
为使闭环极点位于希望的位置,计算超前滞后校正中超前部分应产生的超前相角:
φ c = ± ( 2 k + 1 ) π − ∠ G 0 ( s d ) \varphi_c=±(2k+1)\pi-\angle{G_0(s_d)} φc=±(2k+1)π−∠G0(sd) -
超前滞后校正装置的传递函数为:
φ c = ± ( 2 k + 1 ) π − ∠ G 0 ( s d ) , G c ( s ) = K c ( s + 1 T 1 s + β T 1 ) ( s + 1 T 2 s + 1 T 2 β ) \varphi_c=±(2k+1)\pi-\angle{G_0(s_d)},G_c(s)=K_c\left(\frac{s+\displaystyle\frac{1}{T_1}}{s+\displaystyle\frac{\beta}{T_1}}\right)\left(\frac{s+\displaystyle\frac{1}{T_2}}{s+\displaystyle\frac{1}{T_2\beta}}\right) φc=±(2k+1)π−∠G0(sd),Gc(s)=Kc s+T1βs+T11 s+T2β1s+T21 -
对超前滞后校正中滞后部分的 T 2 T_2 T2选择要足够大,即:
∣ s d + 1 T 2 s d + 1 T 2 β ∣ = 1 , ∣ s d + 1 T 1 s d + β T 1 ∣ ∣ K 1 G 0 ( s d ) ∣ = 1 , ∠ ( s d + 1 T 1 ) − ∠ ( s d + β T 1 ) = φ \begin{vmatrix} \displaystyle\frac{s_d+\displaystyle\frac{1}{T_2}}{s_d+\displaystyle\frac{1}{T_2\beta}} \end{vmatrix}=1,\begin{vmatrix} \displaystyle\frac{s_d+\displaystyle\frac{1}{T_1}}{s_d+\displaystyle\frac{\beta}{T_1}} \end{vmatrix}\begin{vmatrix}K_1G_0(s_d)\end{vmatrix}=1,\angle\left(s_d+\displaystyle\frac{1}{T_1}\right)-\angle\left(s_d+\displaystyle\frac{\beta}{T_1}\right)=\varphi sd+T2β1sd+T21 =1, sd+T1βsd+T11 K1G0(sd) =1,∠(sd+T11)−∠(sd+T1β)=φ -
利用求得的 β \beta β值,选择 T 2 T_2 T2,使:
∣ s d + 1 T 2 s d + 1 T 2 β ∣ ≈ 1 , 0 ° < ∠ ( s d + 1 T 2 s d + 1 T 2 β ) < 3 ° \begin{vmatrix} \displaystyle\frac{s_d+\displaystyle\frac{1}{T_2}}{s_d+\displaystyle\frac{1}{T_2\beta}} \end{vmatrix}≈1,0°<\angle\left(\frac{s_d+\displaystyle\frac{1}{T_2}}{s_d+\displaystyle\frac{1}{T_2\beta}}\right)<3° sd+T2β1sd+T21 ≈1,0°<∠ sd+T2β1sd+T21 <3° -
检验性能指标。
3.5 MATLAB/SIMULINK在根轨迹法校正中的应用
3.5.1 实战1:超前校正
实验要求:已知控制系统开环传递函数为: G ( s ) = 2.3 s ( 1 + 0.2 s ) ( 1 + 0.15 s ) G(s)=\displaystyle\frac{2.3}{s(1+0.2s)(1+0.15s)} G(s)=s(1+0.2s)(1+0.15s)2.3,设计超前校正环节,使其校正后系统的静态速度误差系数 K v ≤ 4.6 K_v≤4.6 Kv≤4.6,闭环主导极点满足阻尼比 ζ = 0.2 \zeta=0.2 ζ=0.2,自然振荡角频率 ω n = 12.0 r a d / s \omega_n=12.0{\rm rad/s} ωn=12.0rad/s,绘制校正前后系统的单位阶跃响应曲线、单位脉冲响应曲线和根轨迹。
解:
【 S T E P 1 {\rm STEP1} STEP1】:计算串联超前校正环节参数子函数程序设计。
% get_param子函数,文件名:get_param.m
function Gc=get_param(G,s1,kc)
numG=G.num{1};denG=G.den{1};
ngv=polyval(numG,s1);dgv=polyval(denG,s1);
g=ngv/dgv;
theta_G=angle(g);theta_s=angle(s1);
MG=abs(g);Ms=abs(s1);
Tz=(sin(theta_s)-kc*MG*sin(theta_G-theta_s))/(kc*MG*Ms*sin(theta_G));
Tp=-(kc*MG*sin(theta_s)+sin(theta_G+theta_s))/(Ms*sin(theta_G));
Gc=tf([Tz,1],[Tp,1]);
【 S T E P 2 {\rm STEP2} STEP2】:求解系统校正环节传递函数和校正后闭环传递函数及各响应曲线。
% 实例Chapter8.3.5.1
clc;clear;
% 建立校正前控制系统开环传递函数
num=2.3;den=conv([1,0],conv([0.2,1],[0.15,1]));
G=tf(num,den);
% 校正后系统的性能要求
zeta=0.2;wn=12.0;
[num,den]=ord2(wn,zeta);
s=roots(den);
s1=s(1);kc=2;
Gc=get_param(G,s1,kc);
GGc=G*Gc*kc; % 校正后系统开环传递函数
G_bf_close=feedback(G,1); % 校正前系统闭环传递函数
G_af_close=feedback(GGc,1); % 校正后系统闭环传递函数
% 绘制单位阶跃响应
figure(1);
step(G_af_close,'b',3.5);hold on;
step(G_bf_close,'r',3.5);grid;
legend('校正后闭环系统阶跃响应','校正前闭环系统阶跃响应');
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('校正前后系统阶跃响应','FontSize',15);
% 绘制单位脉冲响应
figure(2);
impulse(G_af_close,'b',3.5);hold on;
impulse(G_bf_close,'r',3.5);grid;
legend('校正后闭环系统脉冲响应','校正前闭环系统脉冲响应');
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('校正前后系统脉冲响应','FontSize',15);
% 绘制校正前后系统根轨迹图
figure(3);
rlocus(G,GGc);grid;
legend('校正前系统根轨迹图','校正后系统根轨迹图');
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('校正前后系统根轨迹','FontSize',15);
% 超前校正环节传递函数和校正后系统闭环传递函数
Gc,G_af_close
% 校正环节传递函数
Gc =
1.016 s + 1
------------
0.0404 s + 1
% 校正后系统闭环传递函数
G_af_close =
4.672 s + 4.6
-------------------------------------------------------
0.001212 s^4 + 0.04414 s^3 + 0.3904 s^2 + 5.672 s + 4.6
【 S T E P 3 {\rm STEP3} STEP3】:系统校正前后单位阶跃响应曲线。

【 S T E P 4 {\rm STEP4} STEP4】:系统校正前后单位脉冲响应曲线。

【 S T E P 5 {\rm STEP5} STEP5】:系统校正前后根轨迹。

【 S T E P 6 {\rm STEP6} STEP6】:性能分析。
- 串联超前校正环节传递函数为: G c ( s ) = 1.016 s + 1 0.0404 s + 1 G_c(s)=\displaystyle\frac{1.016s+1}{0.0404s+1} Gc(s)=0.0404s+11.016s+1;
- 由单位阶跃响应曲线知,校正前系统超调: σ = 17.3 % \sigma=17.3\% σ=17.3%,上升时间: t r = 0.58 s t_r=0.58{\rm s} tr=0.58s,调节时间: t s = 2.92 s t_s=2.92{\rm s} ts=2.92s;
- 由单位阶跃响应曲线知,校正后系统超调: σ = 31.7 % \sigma=31.7\% σ=31.7%,上升时间: t r = 0.123 s t_r=0.123{\rm s} tr=0.123s,调节时间: t s = 2.3 s t_s=2.3{\rm s} ts=2.3s;
- 因此,系统经串联超前校正后,系统性能提高;
- 从根轨迹图知,校正后系统根轨迹左移,提高系统相对稳定性,缩短系统调节时间;
3.5.2 实战2:滞后校正
实验要求:已知系统开环传递函数为: G ( s ) = 4 s ( s + 2.5 ) G(s)=\displaystyle\frac{4}{s(s+2.5)} G(s)=s(s+2.5)4,设计串联滞后校正环节,使其校正后系统的静态速度误差系数: K v ≤ 6 K_v≤6 Kv≤6,闭环主导极点满足阻尼比: ζ = 0.407 \zeta=0.407 ζ=0.407,绘制校正前后系统单位阶跃响应曲线、单位脉冲响应、根轨迹。
解:
【 S T E P 1 {\rm STEP1} STEP1】:计算串联滞后校正环节参数子函数程序设计。
% get_param_02子函数,文件:get_param_02.m
function [Gc,kc]=get_param_02(G,zeta,wc,Tz)
G=tf(G);[r,k]=rlocus(G);
za=zeta/sqrt(1-zeta^2);
ri=r(1,find(imag(r(1,:))>0));
ra=imag(ri)./real(ri);
kc=spline(ra,k(find(imag(r(1,:))>0)),1/za);
syms x;syms ng;syms dg;
ng=poly2sym(G.num{1});dg=poly2sym(G.den{1});
ess=limit(ng*kc/dg*x);
beta=round(100/sym2poly(ess)/wc);Tp=Tz/beta;
Gc=tf([1,Tz],[1,Tp]);
【 S T E P 2 {\rm STEP2} STEP2】:求解系统校正环节传递函数和校正后闭环传递函数及各响应曲线。
% 实例Chapter8.3.5.2
clc;clear;
% 建立校正前控制系统开环传递函数
num=4;den=conv([1,0],[1,2.5]);
G=tf(num,den);
% 校正后系统的性能要求
zeta=0.407;wc=6;Tz=0.1;
[Gc,Kc]=get_param_02(G,zeta,wc,Tz);
GGc=G*Gc*Kc; % 校正后系统开环传递函数
G_bf_close=feedback(G,1); % 校正前系统闭环传递函数
G_af_close=feedback(GGc,1); % 校正后系统闭环传递函数
% 绘制单位阶跃响应
figure(1);
step(G_af_close,'b');hold on;
step(G_bf_close,'r');grid;axis([0 15 0 1.4]);
legend('校正后闭环系统阶跃响应','校正前闭环系统阶跃响应');
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('校正前后系统阶跃响应','FontSize',15);
% 绘制单位脉冲响应
figure(2);
impulse(G_af_close,'b');hold on;
impulse(G_bf_close,'r');grid;
legend('校正后闭环系统脉冲响应','校正前闭环系统脉冲响应');
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('校正前后系统脉冲响应','FontSize',15);
% 绘制校正前后系统根轨迹图
figure(3);
rlocus(G,GGc);grid;
legend('校正前系统根轨迹图','校正后系统根轨迹图');
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('校正前后系统根轨迹','FontSize',15);
% 超前校正环节传递函数和校正后系统闭环传递函数
Gc,Kc,G_af_close
% 滞后校正环节传递函数
Gc =
s + 0.1
---------
s + 0.025
% 系统增益
Kc =
2.3581
% 校正后系统闭环传递函数
G_af_close =
9.433 s + 0.9433
----------------------------------
s^3 + 2.525 s^2 + 9.495 s + 0.9433
【 S T E P 3 {\rm STEP3} STEP3】:系统校正前后单位阶跃响应曲线。

【 S T E P 4 {\rm STEP4} STEP4】:系统校正前后单位脉冲响应曲线。

【 S T E P 5 {\rm STEP5} STEP5】:系统校正前后根轨迹。

【 S T E P 6 {\rm STEP6} STEP6】:性能分析。
- 串联滞后校正环节传递函数为: G c ( s ) = s + 0.1 s + 0.025 G_c(s)=\displaystyle\frac{s+0.1}{s+0.025} Gc(s)=s+0.025s+0.1;
- 由单位阶跃响应曲线知,校正前系统超调: σ = 8.08 % \sigma=8.08\% σ=8.08%,上升时间: t r = 0.961 s t_r=0.961{\rm s} tr=0.961s,调节时间: t s = 2.99 s t_s=2.99{\rm s} ts=2.99s;
- 由单位阶跃响应曲线知,校正后系统超调: σ = 27.4 % \sigma=27.4\% σ=27.4%,上升时间: t r = 0.478 s t_r=0.478{\rm s} tr=0.478s,调节时间: t s = 2.3 s t_s=2.3{\rm s} ts=2.3s;
- 因此,系统经串联滞后校正后,系统性能提高;
3.5.3 实战3:超前滞后校正环节
实验要求:已知系统开环传递函数为: G ( s ) = 8 s ( s + 0.4 ) G(s)=\displaystyle\frac{8}{s(s+0.4)} G(s)=s(s+0.4)8,设计超前滞后校正环节,使其校正后系统的静态速度误差系数: K v ≤ 5 K_v≤5 Kv≤5,闭环主导极点满足阻尼比: ζ = 0.2 \zeta=0.2 ζ=0.2和自然振荡角频率: ω n = 5 r a d / s \omega_n=5{\rm rad/s} ωn=5rad/s,相角裕度为: 50 ° 50° 50°,绘制校正前后系统的单位阶跃响应曲线、单位脉冲响应曲线和根轨迹。
解:
【 S T E P 1 {\rm STEP1} STEP1】:主函数。
% 实例Chapter8.3.5.3
clc;clear;
% 建立控制系统模型
z=[];p=[0,-0.4];k=8;
Gz=zpk(z,p,k);G=tf(Gz);
zeta=0.2;wn=5;
kc=1;Tz=0.1;dPm=50+5;
ng=G.num{1}; % 把G.num中的第一个元胞赋给ng.
[num,den]=ord2(wn,zeta);
s=roots(den);
s1=s(1);
Gc1=get_param(G,s1,kc);
G1=G*Gc1*kc;
[Gc2,Kc2]=get_param_02(G,zeta,wn,Tz);
GGc=G1*Gc2*Kc2; % 校正后系统开环传递函数
G_bf_close=feedback(G,1); % 校正前系统闭环传递函数
G_af_close=feedback(GGc,1); % 校正后系统闭环传递函数
% 绘制单位阶跃响应
figure(1);
step(G_af_close,'b');hold on;
step(G_bf_close,'r');grid;
legend('校正后闭环系统阶跃响应','校正前闭环系统阶跃响应');
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('校正前后系统阶跃响应','FontSize',15);
% 绘制单位脉冲响应
figure(2);
impulse(G_af_close,'b');hold on;
impulse(G_bf_close,'r');grid;
legend('校正后闭环系统脉冲响应','校正前闭环系统脉冲响应');
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('校正前后系统脉冲响应','FontSize',15);
% 绘制校正前后系统根轨迹图
figure(3);
rlocus(G,GGc);grid;
legend('校正前系统根轨迹图','校正后系统根轨迹图');
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('校正前后系统根轨迹','FontSize',15);
% 超前校正环节传递函数和校正后系统闭环传递函数
Gc1,Gc2,G_af_close
【 S T E P 2 {\rm STEP2} STEP2】:超前环节传递函数、滞后环节传递函数和校正后闭环传递函数。
% 超前校正环节传递函数
Gc1 =
1.358 s + 1
-----------
0.425 s + 1
% 滞后校正环节传递函数
Gc2 =
s + 0.1
----------
s + 0.0125
% 校正后系统闭环传递函数
G_af_close =
1.358 s^2 + 1.136 s + 0.1
-------------------------------------------------
0.425 s^4 + 1.175 s^3 + 1.773 s^2 + 1.141 s + 0.1
【 S T E P 3 {\rm STEP3} STEP3】:单位阶跃响应曲线。

【 S T E P 4 {\rm STEP4} STEP4】:单位脉冲响应曲线。

【 S T E P 5 {\rm STEP5} STEP5】:系统根轨迹曲线。
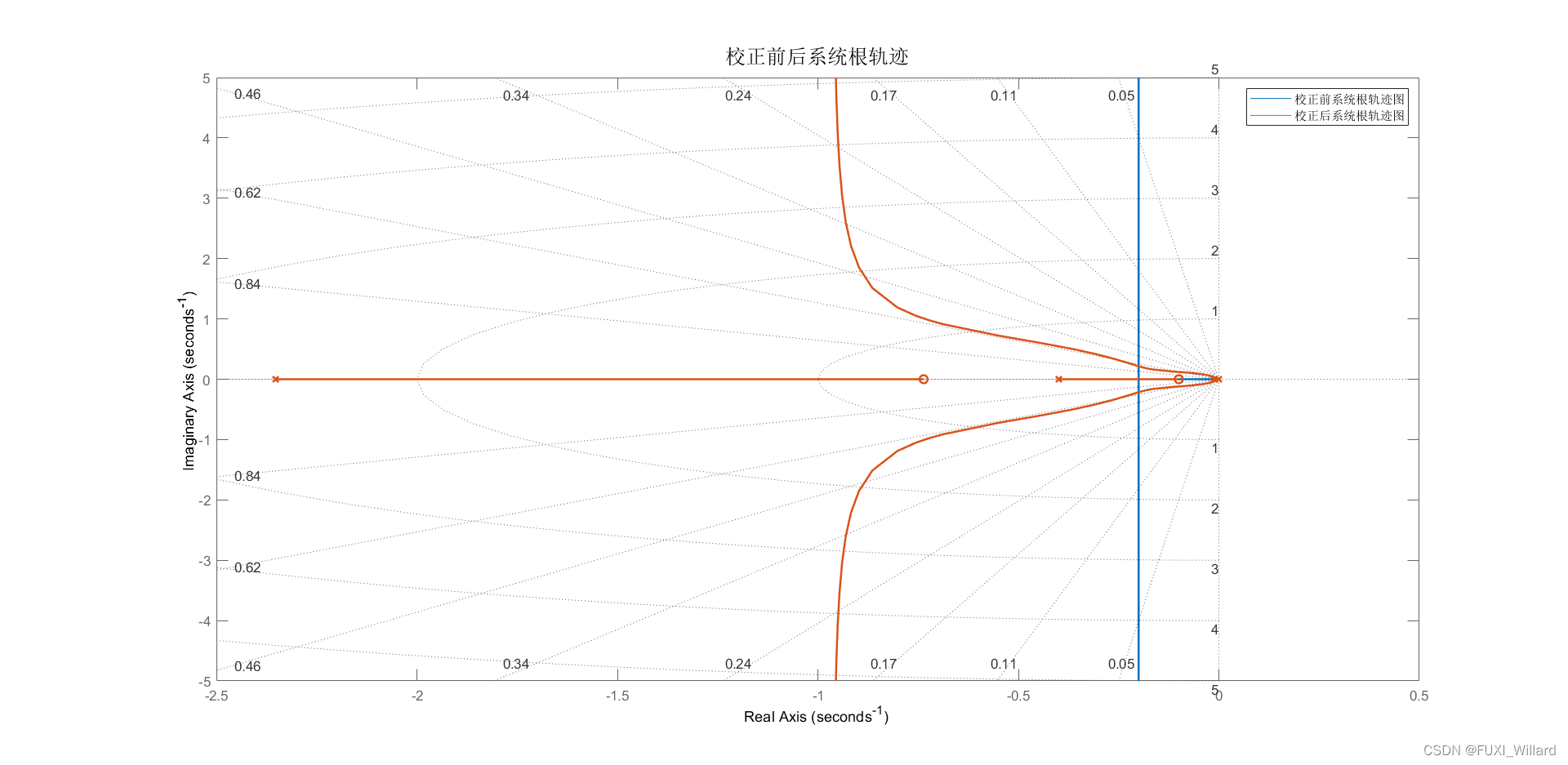
【 S T E P 6 {\rm STEP6} STEP6】:系统性能分析。
- 串联超前滞后校正环节传递函数为: G c ( s ) = 0.125 × s + 0.1 s + 0.0125 × 1.358 s + 1 0.425 s + 1 G_c(s)=0.125\times\displaystyle\frac{s+0.1}{s+0.0125}\times\displaystyle\frac{1.358s+1}{0.425s+1} Gc(s)=0.125×s+0.0125s+0.1×0.425s+11.358s+1;
- 由单位阶跃响应曲线知,校正前系统超调: σ = 79.9 % \sigma=79.9\% σ=79.9%,上升时间: t r = 0.384 s t_r=0.384{\rm s} tr=0.384s,调节时间: t s = 19.1 s t_s=19.1{\rm s} ts=19.1s;
- 由单位阶跃响应曲线知,校正后系统超调: σ = 28.9 % \sigma=28.9\% σ=28.9%,上升时间: t r = 0.907 s t_r=0.907{\rm s} tr=0.907s,调节时间: t s = 4.19 s t_s=4.19{\rm s} ts=4.19s;
- 因此,系统经串联超前滞后校正后,系统性能提高;
