一学就会:A*算法详细介绍(Python)
📢本篇文章是博主人工智能学习以及算法研究时,用于个人学习、研究或者欣赏使用,并基于博主对相关等领域的一些理解而记录的学习摘录和笔记,若有不当和侵权之处,指出后将会立即改正,还望谅解。文章分类在👉启发式算法专栏:
【人工智能】- 【启发式算法】(6)---《一学就会:A*算法详细介绍(Python)》
一学就会:A*算法详细介绍(Python)
目录
A*算法介绍
A*算法的核心概念
A*算法的特点
A*算法示例:迷宫
执行步骤
第1步:初始化
第2步:扩展当前节点(起始节点)
第3步:选择下一个节点(最低 f(n))
第4步:处理当前节点 (0,1)
第5步:继续探索
重点说明
最终结果
A*算法与其他相关算法的比较
[Python] A*算法实现
[Results] 运行结果
[Notice] 注意事项
适用场景
实现建议
A*算法介绍
A*算法是一种高效的路径搜索算法,广泛应用于人工智能、机器人技术、游戏开发等领域。它由Peter Hart、Nils Nilsson和Bertram Raphael于1968年首次提出。A算法结合了Dijkstra算法的系统性搜索和启发式搜索的优点,通过使用启发式函数来减少搜索空间,同时保证找到最短路径。
A*算法的核心概念
A*算法是一种最佳优先搜索算法,它通过以下三个关键函数来评估路径:
-
g(n):从起点到当前节点的实际代价。
-
h(n):从当前节点到目标节点的启发式估算代价。
-
f(n) = g(n) + h(n):通过当前节点到达目标的总估算代价。
在每次迭代中,A*算法会选择具有最低f(n)值的节点进行扩展,并更新其邻居节点的代价。如果邻居节点的试探性代价低于之前记录的值,则会更新该节点的代价,并将其添加到开放集合中。这一过程会持续进行,直到找到目标节点或确定路径不存在。
A*算法的特点
-
最优性:当使用可接受的启发式函数时,A*算法能够找到最短路径。
-
效率:启发式函数的引导使得A*算法比Dijkstra算法探索更少的节点。
-
灵活性:启发式函数可以根据不同场景进行定制。
-
完整性:如果存在解决方案,A*算法将找到它。
A*算法示例:迷宫
以下是使用A*算法在一个示例迷宫中寻找路径的详细步骤说明:
假设有以下10x10的迷宫:
S 0 0 0 0 0 0 0 0 0
0 1 1 0 1 1 0 1 1 0
0 1 0 0 0 0 0 0 1 0
0 1 1 1 1 1 0 1 1 0
0 0 0 0 1 0 0 0 0 0
0 1 1 0 1 1 1 1 1 0
0 1 0 0 0 0 0 0 0 0
0 1 1 1 1 1 1 1 1 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 E其中,S 表示起点 (0,0),E 表示终点 (9,9),0 表示可以通行的路径,1 表示障碍物.
执行步骤
第1步:初始化
-
起始节点:
(0,0),初始化其g(n)=0,h(n)由直线距离计算,f(n)=0+13.416=13.416。 -
开放列表:未被选择的节点。
-
封闭列表:已被选择的节点。
-
当前节点:起始节点。
第2步:扩展当前节点(起始节点)
-
邻节点:
(0,1),(1,0)。 -
检查范围:确保邻节点在迷宫范围内。
-
障碍物检查:
(0,1)是0,(1,0)是0。 -
计算邻节点
g(n):-
(0,1):起始节点的g(n)=0+1=1。 -
(1,0):起始节点的g(n)=0+1=1。
-
-
计算邻节点
h(n):-
(0,1)的h(n)=sqrt((9-0)^2 + (9-1)^2)= sqrt(81+64)=11.401。 -
(1,0)的h(n)=sqrt((9-1)^2 + (9-0)^2)=sqrt(64+81)=11.401。
-
-
计算邻节点
f(n):-
(0,1)的f(n)=1+11.401=12.401。 -
(1,0)的f(n)=1+11.401=12.401。
-
-
在开放列表中添加邻节点:
-
(0,1)和(1,0)添加到开放列表。
-
第3步:选择下一个节点(最低 f(n))
开放列表中有 (0,1) 和 (1,0),它们的 f(n) 都是 12.401。可以选择其中任意一个:
选择 (0,1) 作为当前节点。
第4步:处理当前节点 (0,1)
-
邻节点:
(0,0)(起点,已在封闭列表),(0,2),(1,1)。 -
障碍物检查:
-
(0,2)是0。 -
(1,1)是1(障碍物)。
-
-
生成有效邻节点:
(0,2)。 -
计算
(0,2)的g(n):-
来自
(0,1),g(n)=1+1=2。
-
-
计算
(0,2)的h(n):-
sqrt((9-0)^2 + (9-2)^2)= sqrt(81+49)=10.630。
-
-
计算
(0,2)的f(n):-
2+10.630=12.630。
-
-
将
(0,2)添加到开放列表:-
开放列表现在包含
(1,0), (0,2)。
-
第5步:继续探索
重复步骤,选择开放列表中 f(n) 最低的节点,继续扩展并更新邻节点的 g(h,f) 值,直到到达目标节点 (9,9)。
重点说明
-
扩展当前节点:每次从开放列表中取出
f(n)最低的节点,生成其邻节点。 -
更新邻节点信息:
-
如果邻节点未被访问过,计算其
g(h,f)并加入开放列表。 -
如果邻节点已在开放列表中,需要比较新的
g(n)是否更小。如果更小,更新父节点和g(n)。
-
-
终止条件:
-
当前节点是目标节点,回溯路径。
-
开放列表为空,没有路径。
-
最终结果
经过反复的节点扩展和评估,A* 算法最终找到从起点 (0,0) 到终点 (9,9) 的最短路径。路径将避免迷宫中的所有障碍物,确保每一步都是经过成本最低的选择。
A*算法与其他相关算法的比较
| 算法 | 与A*的关系 | 关键差异 | 优缺点 |
|---|---|---|---|
| Dijkstra算法 | A*是Dijkstra算法的扩展 | A*使用f(n)=g(n)+h(n),Dijkstra仅使用g(n) | A*在有启发式函数时性能更好,Dijkstra无需启发式函数 |
| Bellman-Ford算法 | 基于边的松弛 | Bellman-Ford支持负边权重,A*通常更快 | Bellman-Ford适用于有负权重的图,A*需要启发式函数 |
| Floyd-Warshall算法 | 解决所有点对最短路径问题 | Floyd-Warshall使用动态规划,A*是增量搜索 | Floyd-Warshall适合密集图,A*适合实时路径搜索 |
[Python] A*算法实现
项目代码我已经放入下面链接里面:🔥
A*算法实现
若是下面代码复现困难或者有问题,也欢迎评论区留言。
"""《A*算法实现》
时间:2025.02.27
环境:迷宫
作者:不去幼儿园
"""
import heapq
import matplotlib.pyplot as plt
import numpy as np
class Node:
"""节点类表示搜索树中的每一个点。"""
def __init__(self, parent=None, position=None):
self.parent = parent # 该节点的父节点
self.position = position # 节点在迷宫中的坐标位置
self.g = 0 # G值:从起点到当前节点的成本
self.h = 0 # H值:当前节点到目标点的估计成本
self.f = 0 # F值:G值与H值的和,即节点的总评估成本
# 比较两个节点位置是否相同
def __eq__(self, other):
return self.position == other.position
# 定义小于操作,以便在优先队列中进行比较
def __lt__(self, other):
return self.f < other.f
def astar(maze, start, end):
"""A*算法实现,用于在迷宫中找到从起点到终点的最短路径。"""
start_node = Node(None, start) # 创建起始节点
end_node = Node(None, end) # 创建终点节点
open_list = [] # 开放列表用于存储待访问的节点
closed_list = [] # 封闭列表用于存储已访问的节点
heapq.heappush(open_list, (start_node.f, start_node)) # 将起始节点添加到开放列表
while open_list:
current_node = heapq.heappop(open_list)[1] # 弹出并返回开放列表中 f 值最小的节点
closed_list.append(current_node) # 将当前节点添加到封闭列表
if current_node == end_node: # 如果当前节点是目标节点,则回溯路径
path = []
while current_node:
path.append(current_node.position)
current_node = current_node.parent
return path[::-1] # 返回反向路径,即从起点到终点的路径
(x, y) = current_node.position
neighbors = [(x-1, y), (x+1, y), (x, y-1), (x, y+1)] # 获取当前节点周围的相邻节点
for next in neighbors:
if 0 <= next[0] < maze.shape[0] and 0 <= next[1] < maze.shape[1]: # 确保相邻节点在迷宫范围内
if maze[next[0], next[1]] == 1: # 如果相邻节点是障碍物,跳过
continue
neighbor = Node(current_node, next) # 创建相邻节点
if neighbor in closed_list: # 如果相邻节点已在封闭列表中,跳过不处理
continue
neighbor.g = current_node.g + 1 # 计算相邻节点的 G 值
neighbor.h = ((end_node.position[0] - next[0]) ** 2) + ((end_node.position[1] - next[1]) ** 2) # 计算 H 值
neighbor.f = neighbor.g + neighbor.h # 计算 F 值
if add_to_open(open_list, neighbor): # 如果相邻节点的新 F 值较小,则将其添加到开放列表
heapq.heappush(open_list, (neighbor.f, neighbor))
return None # 如果没有找到路径,返回 None
def add_to_open(open_list, neighbor):
"""检查并添加节点到开放列表。"""
for node in open_list:
if neighbor == node[1] and neighbor.g > node[1].g:
return False
return True # 如果不存在,则返回 True 以便添加该节点到开放列表
def visualize_path(maze, path, start, end):
"""将找到的路径可视化在迷宫上。"""
maze_copy = np.array(maze)
for step in path:
maze_copy[step] = 0.5 # 标记路径上的点
plt.figure(figsize=(10, 10))
plt.imshow(maze_copy, cmap='hot', interpolation='nearest')
path_x = [p[1] for p in path] # 列坐标
path_y = [p[0] for p in path] # 行坐标
plt.plot(path_x, path_y, color='orange', linewidth=2)
start_x, start_y = start[1], start[0]
end_x, end_y = end[1], end[0]
plt.scatter([start_x], [start_y], color='green', s=100, label='Start', zorder=5) # 起点为绿色圆点
plt.scatter([end_x], [end_y], color='red', s=100, label='End', zorder=5) # 终点为红色圆点
plt.legend()
plt.show()
# 设定迷宫的尺寸
maze_size = 100
maze = np.zeros((maze_size, maze_size))
obstacle_blocks = [
(10, 10, 20, 20), # (y起始, x起始, 高度, 宽度)
(30, 40, 20, 30),
(60, 20, 15, 10),
(80, 50, 10, 45),
]
for y_start, x_start, height, width in obstacle_blocks:
maze[y_start:y_start+height, x_start:x_start+width] = 1
start = (0, 0)
end = (92, 93)
maze[start] = 0
maze[end] = 0
path = astar(maze, start, end)
if path:
print("路径已找到:", path)
visualize_path(maze, path, start, end)
else:
print("没有找到路径。")[Results] 运行结果
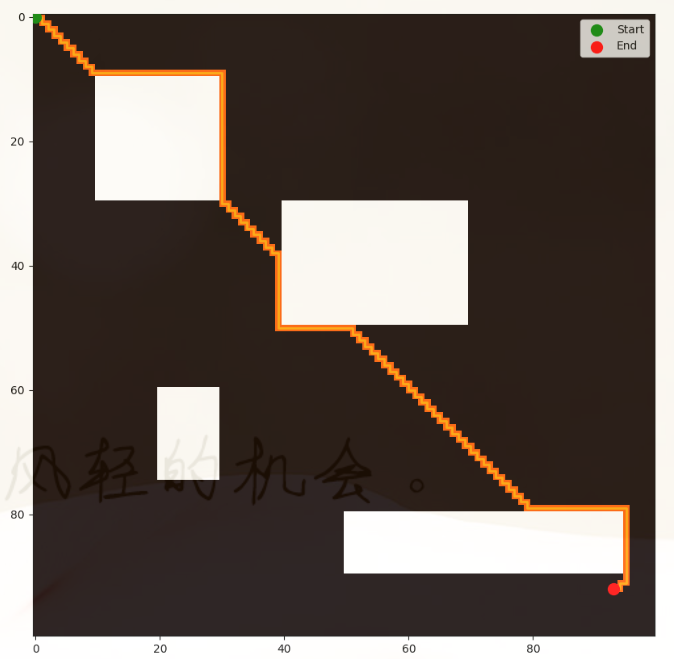
[Notice] 注意事项
# 环境配置
Python 3.11.5
torch 2.1.0
torchvision 0.16.0
gym 0.26.2由于博文主要为了介绍相关算法的原理和应用的方法,缺乏对于实际效果的关注,算法可能在上述环境中的效果不佳或者无法运行,一是算法不适配上述环境,二是算法未调参和优化,三是没有呈现完整的代码,四是等等。上述代码用于了解和学习算法足够了,但若是想直接将上面代码应用于实际项目中,还需要进行修改。
适用场景
A*算法最适合以下场景:
-
单源单目标路径搜索。
-
可以提供领域特定的启发式函数。
-
需要最优解。
-
有足够的内存来维护开放/关闭集合。
主要应用场景
-
迷宫寻路:在游戏开发中,A*算法可以用来为游戏角色找到从起点到终点的最短路径,例如在迷宫类游戏中,角色需要绕过障碍物尽快到达目标。
-
机器人路径规划:在机器人领域,A*算法可用于规划机器人在复杂环境中的移动路径,帮助其避开障碍物并找到到达目标位置的最佳路线。
-
地图导航:在 GPS 导航系统或地图应用中,A*算法可以计算两点之间的最短路径,考虑道路长度、交通状况等多种因素,为用户提供最优的行驶路线建议。
实现建议
-
使用优先队列(如二叉堆或斐波那契堆)快速选择节点。
-
根据图的大小选择合适的数据结构。
-
设计并验证有效的启发式函数。
算法优点
-
寻找最短路径:无论是二维平面还是三维空间,A*算法都能够有效地在复杂的环境图中找到从起点到终点的最短路径,尤其是在具有障碍物和多重路径选择的情况下。
-
优化效率:相比传统的广度优先搜索和深度优先搜索,A*算法通过结合启发式估计和实际路径成本,能够更高效地探索可能的路径,减少不必要的计算,大大提升了路径寻找的效率。
-
适应复杂环境:A*算法能够灵活地处理各种环境变化,如新增障碍物、改变目标位置等,只需重新计算路径即可,无需对整个地图进行重新规划。
实现效果
-
准确性:A*算法能够精确地找到最优路径,确保路径的总成本(如距离、时间等)最小,对于大多数场景来说,其结果都是全局最优的。
-
实时性:在处理复杂地图时,A*算法能够在较短时间内完成路径规划,满足实时性要求,特别是在一些动态环境(如即时战略游戏或动态交通导航)中。
-
可视化:通过可视化工具,可以清晰地看到 A*算法的搜索过程,路径是如何被逐步探索和确定的,这对于调试和理解算法的工作原理非常有帮助。
更多启发式算法文章,请前往:【启发式算法】专栏
博客都是给自己看的笔记,如有误导深表抱歉。文章若有不当和不正确之处,还望理解与指出。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请联系博主删除。如有错误、疑问和侵权,欢迎评论留言联系作者,或者添加VX:Rainbook_2,联系作者。✨
