蓝桥杯第15天(Python版)(数论)
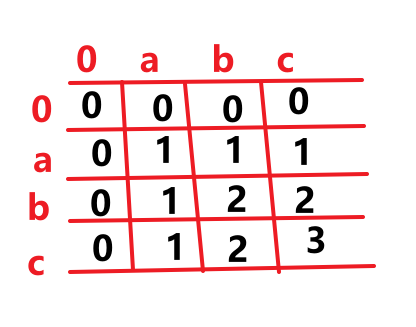
找最长公共子序列模板
import os
import sys
# 请在此输入您的代码
s1=list(input())
s2=list(input())
N=1000
dp=[[0]*N for i in range(N)]
for i in range(1,len(s1)):
for j in range(1,len(s2)):
dp[i][j]=max(dp[i][j-1],dp[i-1][j])
#继承原来的最大值,用max的原因是处理初始情况,即遍历到j=1时的情况的时候
if s1[i]==s2[j]: # 发现相等的就加1
dp[i][j]+=1
print(dp[len(s1)-1][len(s2)-1])合唱队形

要使得出列最少,那么就要留下最多的,我们想到了 LIS ,但是 LIS 只能处理单调序列最长,所以并不能直接用。
我们看到,这里是两头低,中间高的一种情况。
在这种情况下,最多的话那么就是最高的那个人的左侧加上右侧最高。
到这,我们发现。
在中间那个人左侧,从左到右做了一遍 LIS。
在那个人的右侧,从右到左的做了一遍 LIS。
至此,我们好像找了策略。
通过枚举中间那个人,然后看他左侧的LIS和他右侧的LIS的值之和的大小,就能将这道题目解出。
最长递增子序列,用一维数组dp[ ],i遍历[2 - n-1],遍历比i小的s[j],当前dp[ ] 更新为小的s[j]+1
if __name__ == "__main__":
# 输入并赋初值
n = int(input().strip())
t = list(map(int, input().split()))
dp1 = [1] * n
dp2 = [1] * n
# 预处理,从左往右LIS,找最长递增子序列
for i in range(1, n): # 从第二个开始
for j in range(i): # 找i之前比i小的
if t[i] > t[j]:
dp1[i] = max(dp1[i], dp1[j] + 1)
# 预处理,从右往左LIS
for i in range(n - 2, -1, -1): # 从倒数第二个开始
for j in range(n-1, i, -1):
if t[i] > t[j]:
dp2[i] = max(dp2[i], dp2[j] + 1)
maxx = 0
for i in range(n):
maxx = max(maxx, dp1[i] + dp2[i] - 1)
# 自己算了两次,所以-1
print(n - maxx)
字符串编辑距离

def init(s,t):
dp = [[0 for i in range(len(t) + 1)] for j in range(len(s) + 1)]
for i in range(len(s) + 1):
dp[i][0] = 0
for j in range(1,len(t) + 1):
dp[0][j] = 999999
return dp
if __name__ == '__main__':
s = list(input())
t = list(input())
dp=init(s,t)
for i in range(len(s)):
for j in range(len(t)):
if s[i] == t[j]:
dp[i + 1][j + 1] = dp[i][j]
else:
dp[i + 1][j + 1] = min(dp[i][j] + 1, dp[i][j + 1])
dp[i + 1][j + 1] = min( dp[i + 1][j + 1] ,dp[j+1][i]+1)
print(dp[-1][-1])
快速幂


位运算
通过 n&1=True,则n最低位就是1
n>>,n右移动
def fast(a,n,mod):
ans=1
a%=mod # 提升运算效率,Python不用担心大数月越界问题
while(n)>0:
if n&1 :
ans=(a*ans)%mod
#a=a*a # 翻倍
a=(a*a)%mod # 翻倍
n=n>>1 # 右移一位
a,b,mod = map(int,input().split())
print(fast(a,b,mod))最小公倍数公约数
a,b公倍数:
a*b//math.gcd(a,b)
a,b公约数
math.gcd(a,b)
最大最小公倍数



Hankson趣味题

必须从条件2反推,即b1是最大值,遍历[1,sqrt(b1)+1]寻找满足条件的数,注意公倍数,公约数性质,可以用来剪枝,加快运算效率,同时注意判别因子想等情况
36 int(sqrt(36))=6
1*36 2*18 3*12 4*9 6*6 sqrt(36)=6
27 int(sqrt(27))=5
1*27 3*9
答案:

素数筛选
36 int(sqrt(36))=6
1*36 2*18 3*12 4*9 6*6 sqrt(36)=6
27 int(sqrt(27))=5
1*27 3*9

primes = []*N # 记录素数
cnt = 0 # 记录多少个素数
bprime = [False]*N # 标记是否筛选过
def getPrimes (n):
global cnt, primes, bprime
bprime[0] = True
bprime[1] = True
for i in range(2,n+1):
if not bprime[i]: # 找到素数
primes[cnt] = i # 添加记录
cnt +=1
for j in range(i*2,n+1,i): # 晒选以他为因子的
bprime[j] = TrueRSA解密(用到了快速幂运算)

根据关系式反推, e*d ==X(p-1)(q-1)+1,注意n=p*q,p,q为质数,那么n只有这两个因子,没有其他因子,1不是质数
# e*d ==X(p-1)(q-1)+1
#
import math
n=1001733993063167141
d=212353
C=20190324
p=891234941
q=1123984201
e=823816093931522017
# 找p,q
'''for i in range(2,int(math.sqrt(n))+1):
if n%i==0:
print(i,n//i)
'''
# 找e
'''for i in range(2,n+1):
now =i*(p-1)*(q-1)+1
if now % d==0: # 找到了e
print(now//d)
break
'''
# 解密
ans =1
c=C
while e>0:
if e&1:
ans=(ans*c)%n # 取模
c=(c*c)%n # 取模加快运算
e=e>>1 # 记住右移动,不然死循环
print(ans) #记住细心,看清楚记录答案的变量
质因子个数(即判断有多少个质数,任何一个数都能分解为质数的乘积)
知识点



过50%的代码
# 40%
# import math
# def cheak(x):
# for i in range(2,int(math.sqrt(x))+1):
# if x%i==0:
# return False
# return True
# ans=0
# n = int(input())
# for i in range(2,n+1): #约数包括自身
# if n%i==0 and cheak(i): #约数同时是素数
# ans+=1
# print(ans)
# 过80%,只记录第一个出现的约数,第一个出现的约数必定是素数
# 标准模板,质因子分解
# n = int(input())
# ans=0
# i=2
# while i*i<=n:
# if n%i==0:
# ans+=1
# while n%i==0:
# n=n//i
# i+=1
# if n>1:
# ans+=1
# print(ans)阶乘约数


MAXN = 110
cnt = [0] * MAXN #记录对应质数幂次
for i in range(1, 101):
x = i
# 质因子分解
j = 2
while j * j <= x:
if x % j == 0: # 是一个质数约数
while x % j == 0: #类似埃式筛
x //= j
cnt[j] += 1
j += 1
if x > 1:
cnt[x] += 1
ans = 1
for i in range(1, 101):
if cnt[i] != 0:
ans *= (cnt[i] + 1) # 0 也是一种选择
print(ans)最少砝码问题
问题是要求最少砝码个数,那么需要将砝码利用最大化,即增加一个砝码,秤重范围不重复,刚好可以拼接。


砍竹子问题


a=[]
n=int(input())
s=list(map(int,ipnut().split()))
total=0 # 所有竹子砍的次数
cnt=0 #可以少砍的
a.append(set())
for i in range(1,n+1):
h=s[i-1]
a.append(set())
while h >1: # 高度大于1,一直砍
total+=1 # 记录砍的总数
if str(h) in a[i-1]: #当前高度是否在前一个过程中出现
cnt+=1 # 出现就记录,可以少砍一刀
a[i].add(str(h)) #记录当前自己的高度
f(h) #使用魔法