LeetCode222. 完全二叉树的节点个数(二分查找+二进制表示路径法)
一、题目描述
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
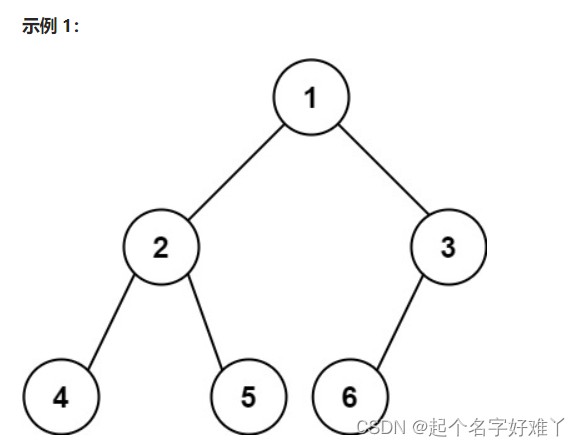
注:
树中节点的数目范围是[0, 5 * 104]
0 <= Node.val <= 5 * 104
题目数据保证输入的树是 完全二叉树
二、题目解析&思路分析
像我拿到这道题,那这还不简单,遍历计数不就搞定了嘛?
前几天刚好复习了二叉树的遍历方法,直接拿出来我最拿手的,也是最基础的 BFS(广度优先遍历,Breath First Search)
基础的二叉树遍历还不太了解的同学可以先看下这篇博客:
数据结构之二叉树构建、广度/深度优先(前序、中序、后序)遍历
话不多说直接上代码分析:
2.1 BFS 广度优先遍历计数法
class Solution {
public:
int countNodes(TreeNode* root) {
int count = 0;//计数器
if(root == nullptr)
{
return count;//空树节点为 0
}
else
{
count = 1;//根节点
}
queue<TreeNode*> quTemp;//利用队列来控制遍历顺序
quTemp.push(root);
while(!quTemp.empty())
{
//依次访问每个节点的左孩子右孩子并计数
TreeNode* nodeTemp = quTemp.front();
quTemp.pop();
if(nodeTemp->left != nullptr)
{
count++;
quTemp.push(nodeTemp->left);
}
if(nodeTemp->right != nullptr)
{
count++;
quTemp.push(nodeTemp->right);
}
}
return count;
}
};
没啥问题,好的提交运行看一下:
有点鸡肋啊,那我们换一种?
2.2 深度优先遍历
深度优先咱们不在此阐述了,不了解的还是照旧看上面的那个博客
咱们还是直接看代码:
class Solution {
public:
int countNodes(TreeNode* root) {
int count = 0;
if(root == nullptr)
{
return count;
}
else
{
DLR(count, root);
return count;
}
}
void DLR(int& count, TreeNode* root)//根左右
{
if(root == nullptr)
{
return;
}
count++;
DLR(count, root->left);
DLR(count, root->right);
}
};
再看运行结果:
leetcode对时间判定还是和电脑设备,网速有一定关系的
深度和广度这两时间上都是(O(n),不过深度优先遍历没有额外用队列来进行辅助,因此空间上是低于BFS的。
难道只能止步于50%多?还有没有更优的解法呢?
2.3 重新解读题目
题目给到的是完全二叉树,那么我们可以知道
完全二叉树:
所有的节点 从 0~n ,从上到下、从左至右,节点都是连续的,先有左孩子才有右孩子节点。
那么这样假设
1.全满节点的二叉树是满二叉树 每一层的节点数都达到最大值,假设树的高度为 h 那么 节点数就是 2^h -1
2.最后一层未满,那么和下图一样最后一个节点肯定在最后一层:
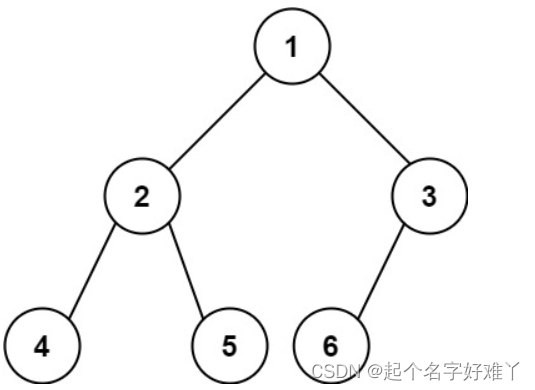
那么我们只需要知道树的高度 和 最后一层的最后一个节点是多少即可知道整颗二叉树的节点数
注:这里题目中没有说节点的值是从上到下,从左到右 是从 1~n 按顺序排列 但是实际上就是如此。
2.4 二分查找 + 二进制表示路径法
由以上分析可以得知我们更优的解法是
需要知道树的高度 和 最后一层的最后一个节点是多少即可知道整颗二叉树的节点数
2.4.1 树的高度
树的高度很容易得出,因为是完全二叉树,那么我们只需要从根节点一直往左孩子遍历即可得知树的高度
int level = 0;//层数 从 0 开始
TreeNode* node = root;
while (node->left != nullptr) {
level++;
node = node->left;
}
2.4.2 二分查找
查找某个值是否存在
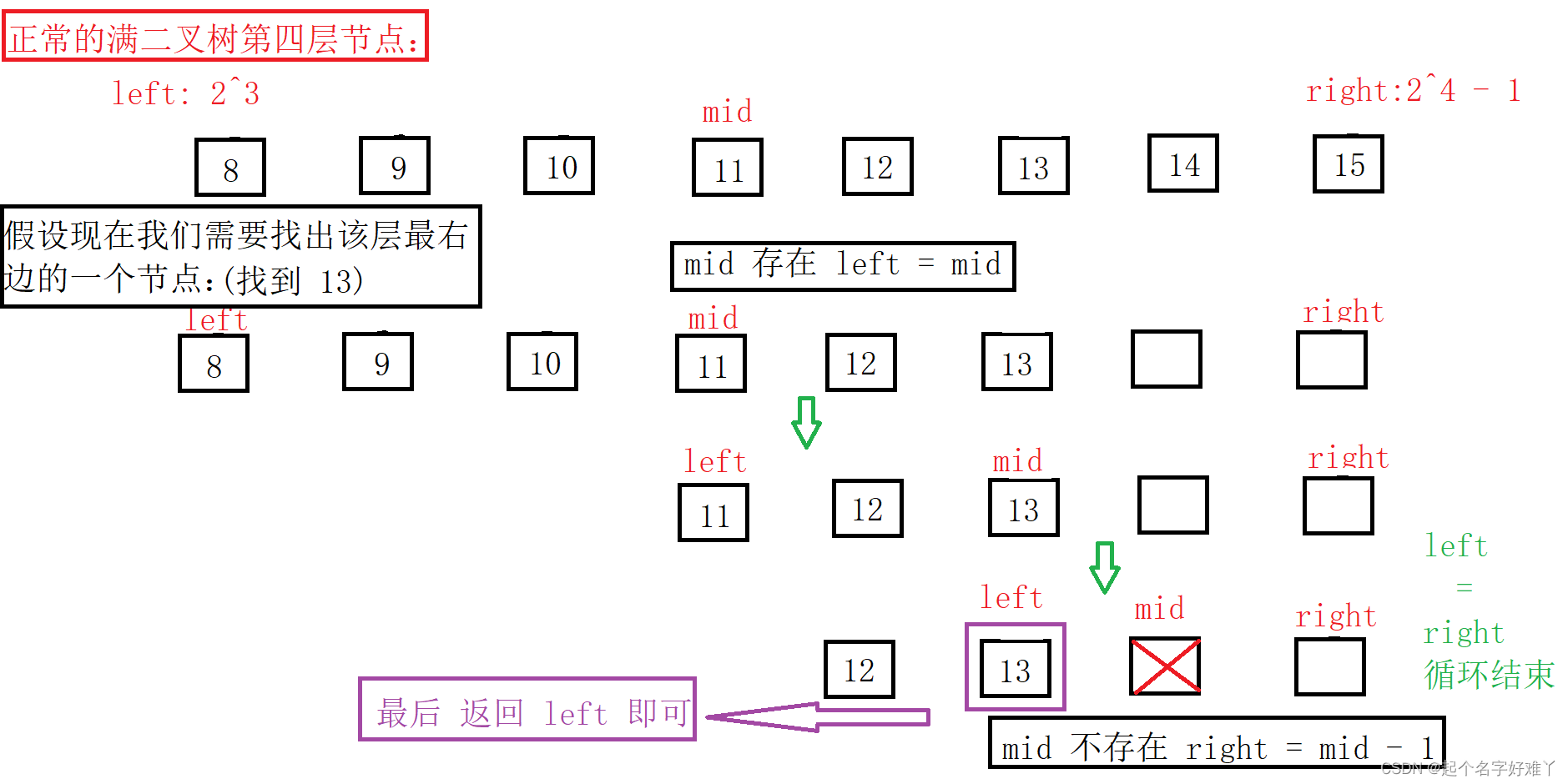
通过二分查找我们就可以知道最右边节点是哪一个,因此可以直接将该值返回,该值就是节点数。
代码实现:
int left = 1 << level, right = (1 << (level + 1)) - 1;
while (left < right)
{
int mid = (right - left + 1) / 2 + left;
if (Is_Exist(root, level, mid))
{
left = mid;
}
else
{
right = mid - 1;
}
}
return left;
但是这里有一个问题,上图讲的是在一个数组中进行值判断,而我们如何判断二叉树得最后一层得节点值是否存在呢?
继续往下看
2.4.3 该数字(节点)是否存在
我们先观察每个节点的值的二进制
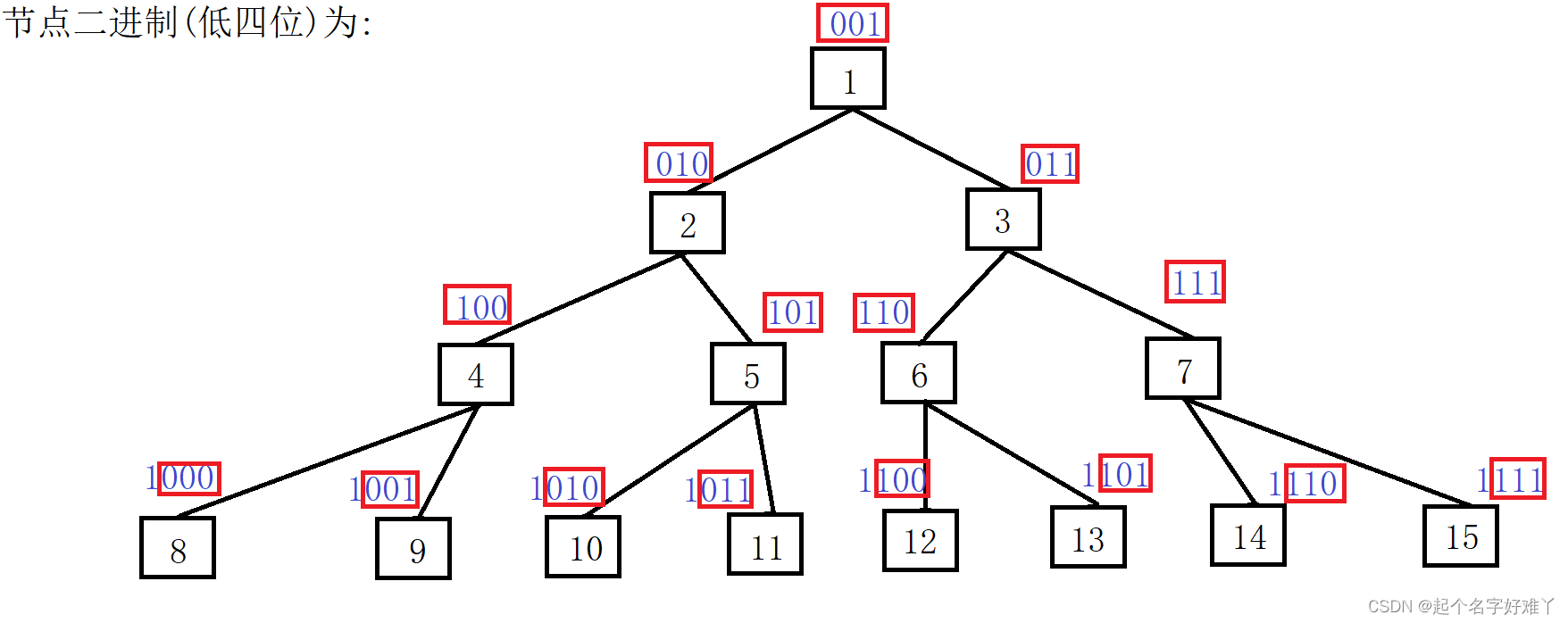
我们根据上图节点得值做出假设:
0 代表向 左
1 代表向 右
总结以下规律:
每个节点的值的部分二进制代表该节点从根节开始走向的路径 例如:
8 :000 代表 从根节点 向左 ->向左 ->向左
11 :011 代表 从根节点 向左 -> 向右 -> 向右
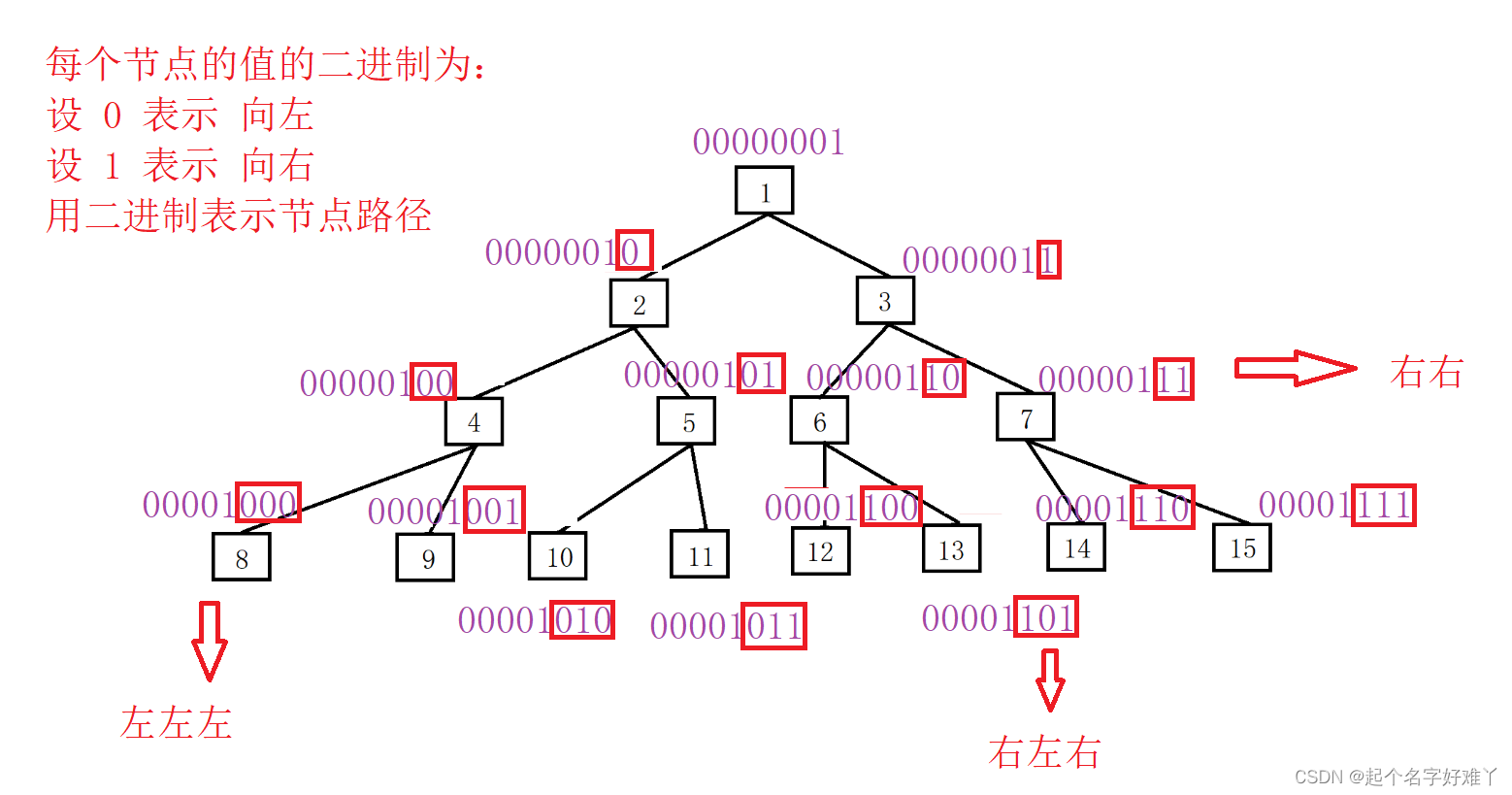
知道 二进制 如何表示 节点的路径之后 我们只需要从左至右逐个把每一位取出来,取出来是 0 就是 从根节点往左走,取出来是 1 表示从根节点往右走,这样一直走下去,最后判断这个节点 node 是不是 nullptr 就可以判断这个节点是不是存在。
代码示例:
bool Is_Exist(TreeNode* root, int level, int k)
{
//例如第 3 层 有 3 个 bit 位表示 路径 那么 就用 0100 按位 & 取即可
int bits = 1 << (level - 1);
TreeNode* node = root;
while (node != nullptr && bits > 0) {
if (bits & k)
{
//是 1 就 往右走
node = node->right;
}
else
{
//是 0 就往左走
node = node->left;
}
//取出来一位判断之后 继续取下一位
bits >>= 1;
}
//最后判断这个节点是不是 nullptr 即可判断该节点存不存在
return node != nullptr;
}
2.4.4 时间复杂度于空间复杂度分析
leetcode 复杂度分析:

三、代码实现
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == nullptr) {
return 0;
}
//二叉树层高从 0 开始
int level = 0;
TreeNode* node = root;
while (node->left != nullptr)
{
level++;
node = node->left;
}
//二分查找最后一层的每个节点是否存在
int left = 1 << level, right = (1 << (level + 1)) - 1;
while (left < right)
{
//每次判断 mid 是否存在
int mid = (right - left + 1) / 2 + left;
if (Is_Exist(root, level, mid))
{
left = mid;
}
else
{
right = mid - 1;
}
}
return left;
}
bool Is_Exist(TreeNode* root, int level, int k)
{
//例如第 3 层 有 3 个 bit 位表示 路径 那么 就用 100 按位 & 取即可
int bits = 1 << (level - 1);
TreeNode* node = root;
while (node != nullptr && bits > 0) {
if (bits & k)
{
//是 1 就 往右走
node = node->right;
}
else
{
//是 0 就往左走
node = node->left;
}
//取出来一位判断之后 继续取下一位
bits >>= 1;
}
//最后判断这个节点是不是 nullptr 即可判断该节点存不存在
return node != nullptr;
}
};
运行结果:可以看到时间效率大幅度提升

