计算机组成原理 --- 数据的表示和运算
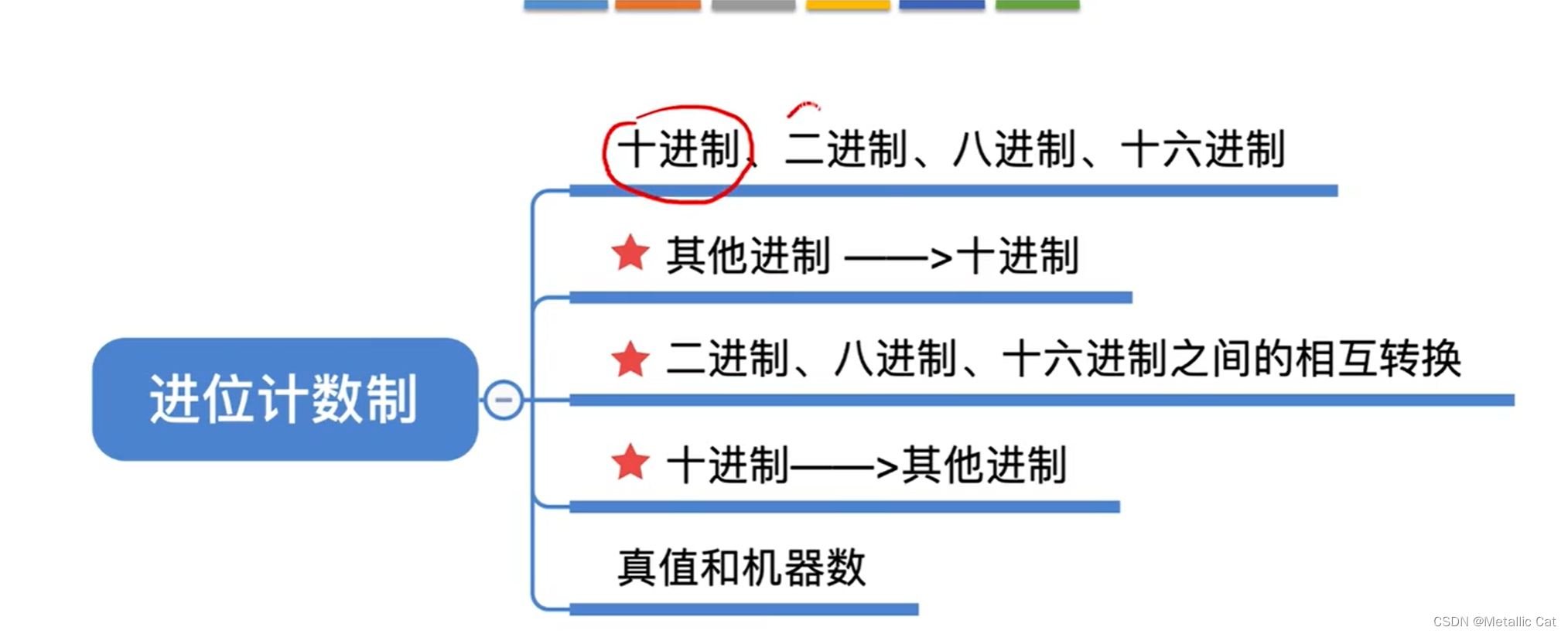
一.进位计数制
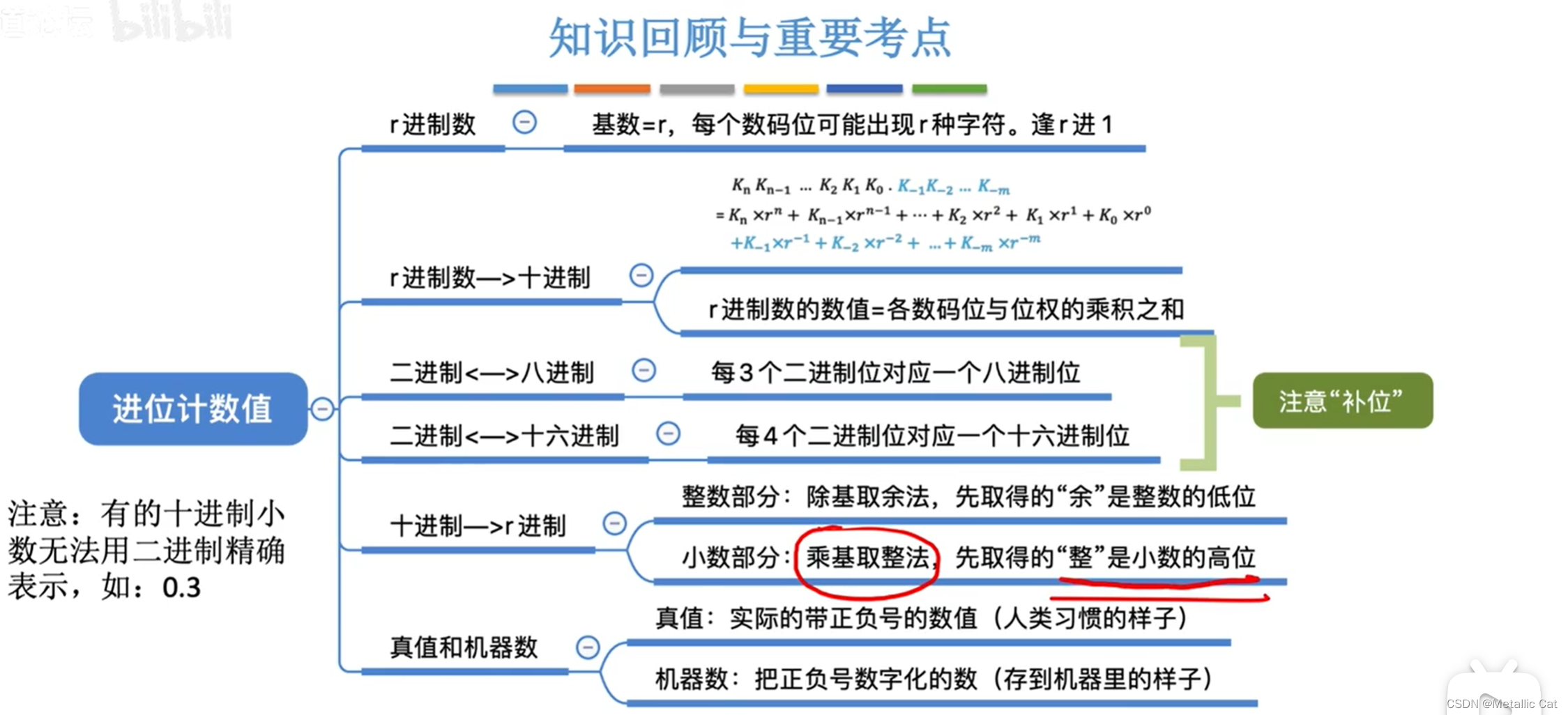
1.由位置确定的权重为位权 --- 比如个位的位权是10的0次方，十位的位权是10的1次方...
1.十进制的基数是 --- 0，1，2，3，4，5，6，7，8，9 ，二进制的基数是0，1....其它同理 
1.规定 --- 在进制中，当数字大于9的时候，就都用大写字母来表示 --- 如A表示10，B表示11... 
1.右边展示的是不同的进制转换为十进制 
2.不同的进制相加有不同的进位 --- 如八进制数则是满八进1，十六进制数相加就是满16进1，n进制数相加就是慢n进1
1.上面的三个理由就是为什么我们选择二进制作为计算机语言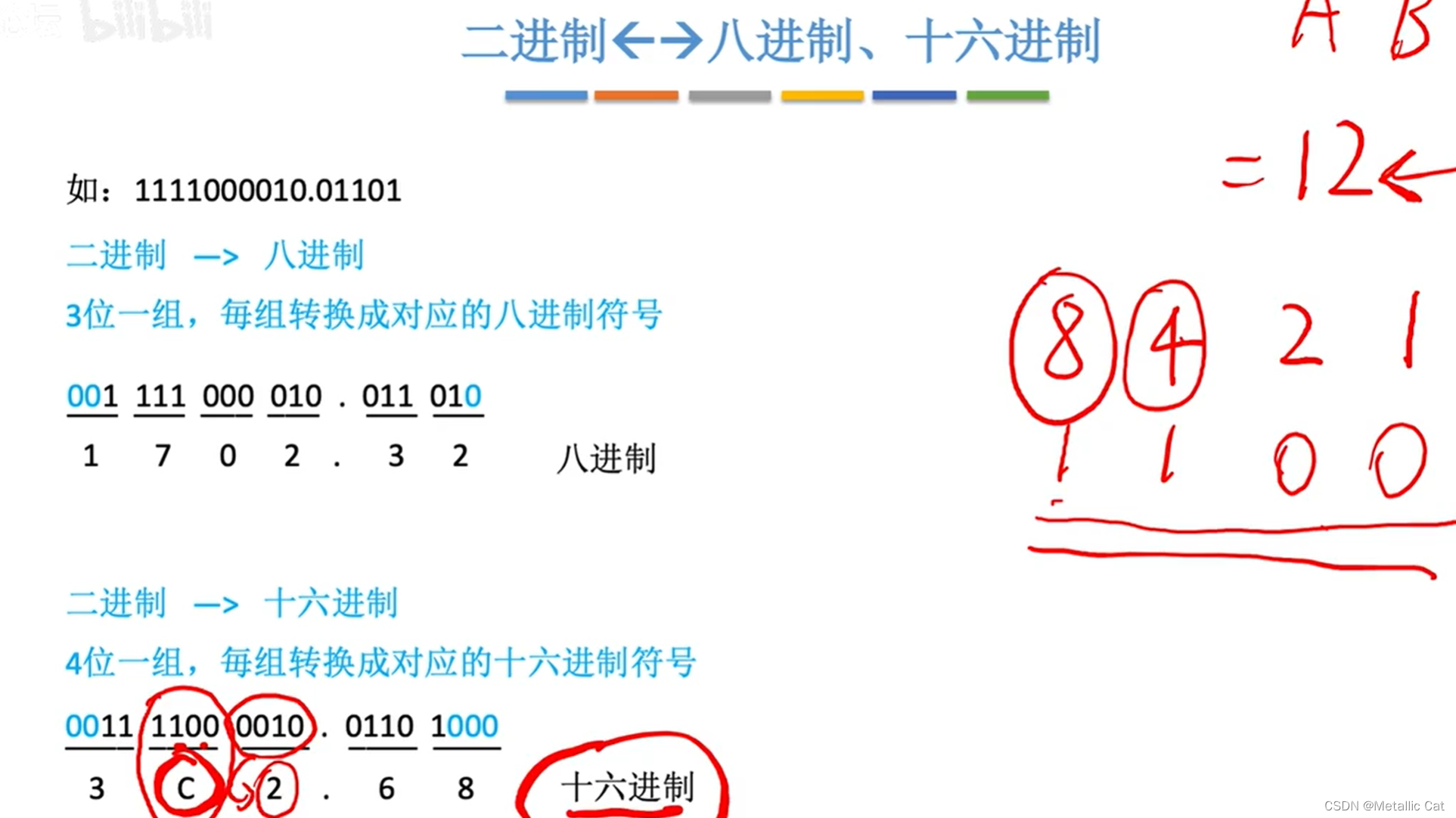 
1.二进制转换为8进制的时候需要明确一个规则就是 --- 每三个二进制数就能够表示一个八进制数（2的3次方等于8，其它的同理 --- 16进制就是每四个2进制数就能够表达，2的4次方等于16 --- 4个二进制数能够表示一个16进制数）
2.转换步骤 --- 以2转8为例 ---从后往前选取三个连续的二进制数（小数点前的和小数点后的是分开来算的，不能混在一起算）（如果不足三个就用0来补充空缺），然后将这三个二进制数转换为对应的十进制数 --- 2的2次方 + 2的1次方 + 2的0次方，每三个二进制数都转换为对应的十进制数之后组合起来的数就是 --- 原来那个二进制数对应的八进制数了（其它同理）
3.整数部分补零是补在头部，小数部分补零是补在尾部
1.八进制，16进制转换为2进制的原理就是 --- 将每一个八进制/十六进制的数转换为对应的二进制数，然后再按顺序组合在一起即可得到其对应的二进制表达。
1.Binary --- 是二进制的意思
2.在数字前面加上0x是表示该数是十六进制数
1.除基取余法的停止条件是除出来的结果中商等于0
1.十进制的小数部分转换为二进制的小数部分的时候常常会出现一种情况 ---- 即十进制的小数无法用二进制的小数精确表示 --- 二进制的小数表达往往只能够不断趋近十进制的小数表达，但无法精确
2.所以在转换的时候我们往往在 --- 第一次出现的小数部分再次出现时停止转换，当然你也可以继续转换下去，不断提高转换精度 
1.所谓的数字化就是增添符号位来让机器能够识别出数字的正负 