当前位置：首页 > article >正文

【图论刷题-6】力扣 797. 所有可能的路径

article 2025/1/19 3:43:37

图论刷题

机器人的运动范围
矩阵中的路径
图像渲染
水位上升的泳池中游泳
寻找图中是否存在路径
所有可能的路径

797. 所有可能的路径

力扣地址：https://leetcode.cn/problems/all-paths-from-source-to-target/

这是一道比较典型的深度优先遍历、广度优先遍历案例，强烈推荐初学者完成这道题并且常常回来看看（也欢迎来看看我的博客 ~ ）

难度：中等

深度优先遍历
广度优先遍历

问题描述

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j] 存在一条有向边）。

示例 1：
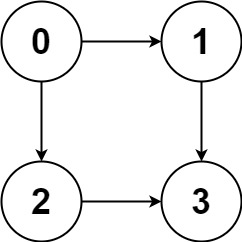
在这里插入图片描述

输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例2：
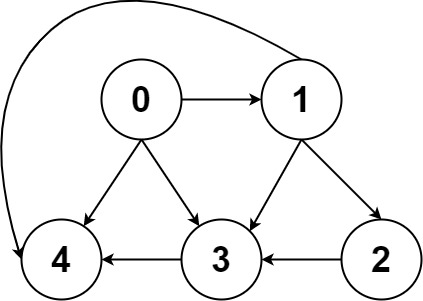
在这里插入图片描述

输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

提示：

n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i（即不存在自环）
graph[i] 中的所有元素互不相同
保证输入为 有向无环图（DAG）

问题分析

理解题目

以示例1 为例，输入的是 graph = [[1,2],[3],[3],[]] ，也就是graph[0] = [1, 2] 表示索引为 0 的点可以到达 1 和 2 两个点，graph[1] = [3] 表示索引为 1 的点可以到达 3。也就是说，graph[i] 即表示索引为 i 的点可以到达的点。

输出结果表示从起点(索引为0) 到终点索引为 n-1 的所有路径。比如这个例子输出的结果为 [[0,1,3],[0,2,3]] 即表示 0 到 3 的所有路径。

引如深度优先遍历

首先回顾一下深度优先遍历的写法，也可以参考一下我们完成的第一道题：机器人的运动范围，接着我们需要确定深度遍历的 遍历规则，也就是 当前点可以到达的下一个点 ，最后我们开始遍历的时候必须指定结束的条件，这个题目中，我们的结束条件就是访问到的点的索引为 n-1。

代码实现

class Solution {
public:
    // 所有的路径
    vector<vector<int>> allWays;
    // 现在走的路
    vector<int> oneWay;
    
    /**
     * 深度遍历图路径，因为是有向无环图所以不用考虑 "走回头路" 这种情况
     * 我们tarvel的目标是前往索引为 n - 1 的点 
     */
    void travel(vector<vector<int>>& graph, int current) {
        // 到达终点
        if (current == graph.size() - 1) {
            allWays.push_back(oneWay);
            return;
        }
        // graph[current] 表示当前点能够去的所有风景区，我们现在每个地方都去看看能不能到终点
        for (auto next : graph[current]) {
            // 记录一下我们当前走的路
            oneWay.push_back(next);
            travel(graph, next);
            // 不管前面的道路有没有到达，我们回到前一个地方
            oneWay.pop_back();
        }
    }
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        oneWay.push_back(0);
        travel(graph, 0);
        return allWays;
    }
};