逆向动力学算法(Python描述)
背景
IK在角色动画的表现中有着很重要的地位。通常的角色动画都是使用FK(Forward kinematics)来进行计算,这种计算方法中父骨骼的变换与子骨骼的变换决定了子骨骼最终的位置。而IK则相反,IK是先决定子骨骼的变换,然后再推导父骨骼需要由此而产生的变换。
就如同人平时的行为一样——往往是手掌的位置和旋转需要先确定(拍到墙壁上的某个点,抓住某个东西等……)后,再进行手肘变换的计算。这也就意味着IK的结算可能产生未知个数的解(0个或多个……),有可能手掌根本抓不到一个地方,或者手掌到了一个地方手肘可以有多个形态和变换。
和机器人控制论很像……不是吗?其实IK结算在机器人的研究中也有很大的作用。
几何分析
如果说骨骼架构比较简单(例如肩->肘->腕,髋->膝->踝等),那么完全可以通过几何分析来进行IK的结算。
例如手臂上臂长度为
l
1
l1
l1,下臂长度为
l
2
l2
l2,再假设每个关节都只有两个旋转自由度,如下图。
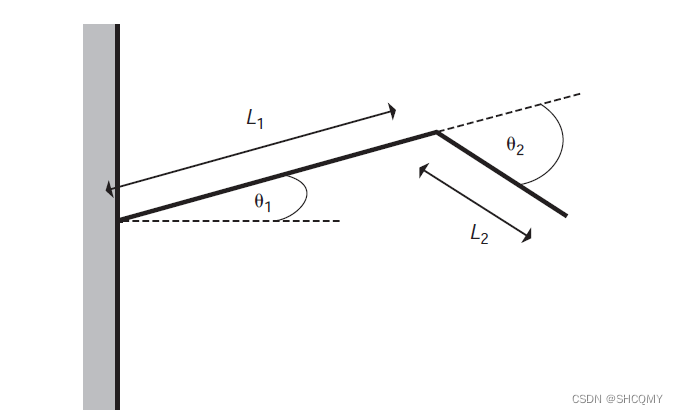
那么最末端的关节便有了一个活动范围(reachable workspace),当结算IK开始的时候,就需要先确保末端关节在这个活动范围内:
∣
L
1
−
L
2
∣
≤
X
2
+
Y
2
≤
L
1
+
L
2
|L_1 - L_2| \leq \sqrt{X^2 + Y^2} \leq L_1 + L_2
∣L1−L2∣≤X2+Y2≤L1+L2
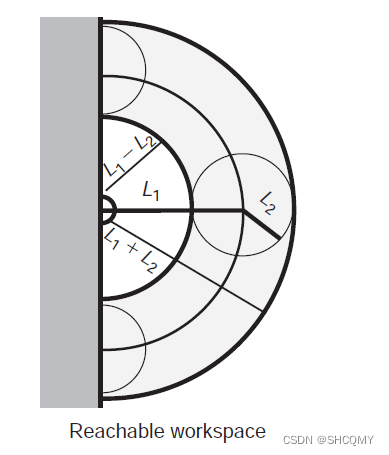
当末端关节的位置确定之后,骨骼架构中对应的两个关节偏转角度
θ
1
θ1
θ1和
θ
2
θ2
θ2就可以通过几何方法确定了。
令尾关节最终位置为
(
X
,
Y
)
(X,Y)
(X,Y),连接首关节和尾关节后,可以分析出最终解应该有两个,这两个解关于直线
(
0
,
0
)
,
(
X
,
Y
)
(0,0),(X,Y)
(0,0),(X,Y)
对称。
最终可以使用余弦定理来计算出最终的
θ
1
θ1
θ1和
θ
2
θ2
θ2,推导过程如下:
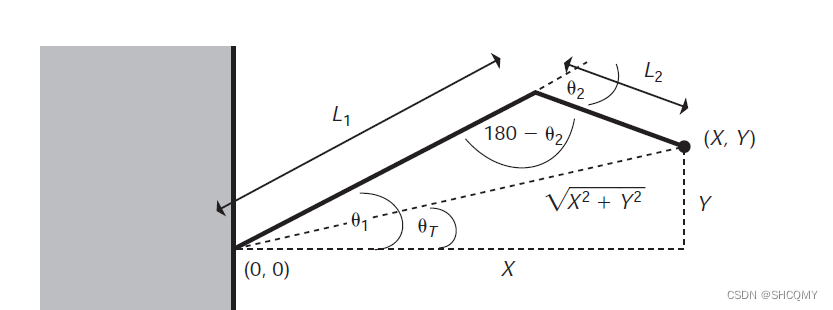
cos
(
θ
T
)
=
X
X
2
+
Y
2
\cos(\theta_T) = \frac{X}{\sqrt{X^2 + Y^2}}
cos(θT)=X2+Y2X
因此有:
θ
T
=
arccos
(
X
X
2
+
Y
2
)
\theta_T = \arccos(\frac{X}{\sqrt{X^2 + Y^2}})
θT=arccos(X2+Y2X)
根据余弦定理:
cos
(
θ
1
−
θ
T
)
=
L
1
2
+
X
2
+
Y
2
−
L
2
2
2
L
1
X
2
+
Y
2
\cos(\theta_1 - \theta_T) = \frac{L_1^2 + X^2 + Y^2 - L_2^2}{2L_1\sqrt{X^2 + Y^2}}
cos(θ1−θT)=2L1X2+Y2L12+X2+Y2−L22
又根据余弦定理:
cos
(
180
−
θ
2
)
=
−
cos
(
θ
2
)
=
L
1
2
+
L
2
2
−
X
2
−
Y
2
2
L
1
L
2
\cos(180 - \theta_2) = -\cos(\theta_2) = \frac{L_1^2 + L_2^2 - X^2 - Y^2}{2L_1L_2}
cos(180−θ2)=−cos(θ2)=2L1L2L12+L22−X2−Y2
有:
θ
2
=
arccos
(
X
2
+
Y
2
−
L
1
2
−
L
2
2
2
L
1
L
2
)
\theta_2 = \arccos(\frac{X^2 + Y^2 - L_1^2 - L_2^2}{2L_1L_2})
θ2=arccos(2L1L2X2+Y2−L12−L22)
这样一来也就获得了
θ
1
θ1
θ1和
θ
2
θ2
θ2的值,需要注意的是
c
o
s
cos
cos函数是偶函数,因此需要考虑到
±
θ
±θ
±θ的情况。实际上,在大多数的游戏中的人形骨骼的IK都是通过这种方式实现的。
在计算出这两个角度之后,就可以直接影响对应的关节位置了。例如机械臂可以进行角度的插值而进行平滑的IK表现,而游戏中则可以直接进行设置。
Cyclic Coordinate Descent(CCD) IK
ccd即循环坐标下降,相关论文 Making Kine More Flexible
这种方法的好处是计算简单而且速度快,并且能够很好的适配骨骼的原本约束,缺点则是最终效果可能并非完全尽如人意,有可能会产生扭曲的关节。游戏《孢子》中的骨骼IK结果就是使用CCD来进行计算的。
具体实现的方法如下:
从骨骼链上最深的子骨节开始进行处理,将这段骨节相对于原点进行旋转从而使它指向效应点。
将这个骨节的父节点针对于原点进行旋转,以使得此父骨节的原点到新旋转的子骨节端点的连线指向效应点即可。
对每个骨节进行1~2步骤的处理。
上述步骤进行多次循环从而得到更加稳定的值。
效应图如下:
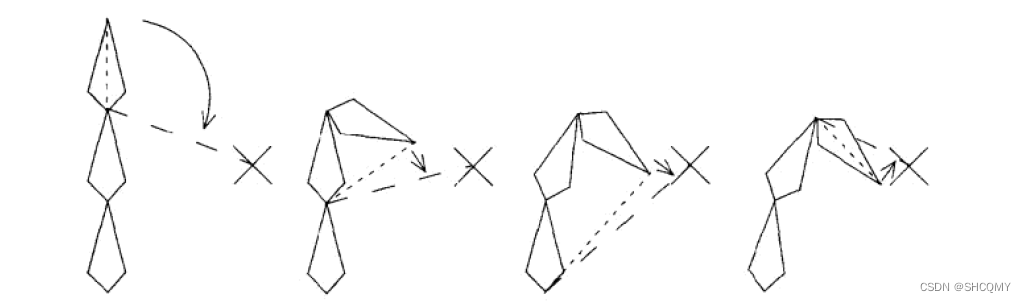
一般来说骨骼的运动是有约束的(例如肘部的可旋转角度一般不会超过180°,如果你可以,我们不妨做个朋友……),因此可以在进行上述步骤1时进行约束。
当然,越严格的约束就意味着需要更多次的迭代处理才能获得一个比较稳定的值。
雅克比矩阵
在IK结算中,如果骨骼的架构比较复杂,那么往往几何分析的结算方法就不太现实了。此时通常使用数值方法让其自己构建出来 —— 在每个时间步长的时候进行对应的计算来得到此时每一个骨节的角度应该进行怎样的改变。在这些数值方法中比较好用的就是使用雅可比矩阵(Jacobian)来进行结算。
从数学意义上来解释雅可比矩阵,我们可以想象有6个函数,每个函数对应着有6个变量。那么针对每个输入变量
x
i
x_i
xi,就会能够得到对应的
y
i
y_i
yi
.
y
1
=
f
1
(
x
1
,
x
2
,
x
3
,
x
4
,
x
5
,
x
6
)
y_1 = f_1(x_1, x_2, x_3, x_4, x_5, x_6)
y1=f1(x1,x2,x3,x4,x5,x6)
y
2
=
f
2
(
x
1
,
x
2
,
x
3
,
x
4
,
x
5
,
x
6
)
y_2 = f_2(x_1, x_2, x_3, x_4, x_5, x_6)
y2=f2(x1,x2,x3,x4,x5,x6)
y
3
=
f
3
(
x
1
,
x
2
,
x
3
,
x
4
,
x
5
,
x
6
)
y_3 = f_3(x_1, x_2, x_3, x_4, x_5, x_6)
y3=f3(x1,x2,x3,x4,x5,x6)
y
4
=
f
4
(
x
1
,
x
2
,
x
3
,
x
4
,
x
5
,
x
6
)
y_4 = f_4(x_1, x_2, x_3, x_4, x_5, x_6)
y4=f4(x1,x2,x3,x4,x5,x6)
y
5
=
f
5
(
x
1
,
x
2
,
x
3
,
x
4
,
x
5
,
x
6
)
y_5 = f_5(x_1, x_2, x_3, x_4, x_5, x_6)
y5=f5(x1,x2,x3,x4,x5,x6)
y
6
=
f
6
(
x
1
,
x
2
,
x
3
,
x
4
,
x
5
,
x
6
)
y_6 = f_6(x_1, x_2, x_3, x_4, x_5, x_6)
y6=f6(x1,x2,x3,x4,x5,x6)
因此
y
i
y_i
yi的导数可以被写成
d
y
i
=
∂
f
i
∂
x
1
d
x
1
+
∂
f
i
∂
x
2
d
x
2
+
∂
f
i
∂
x
3
d
x
3
+
∂
f
i
∂
x
4
d
x
4
+
∂
f
i
∂
x
5
d
x
5
+
∂
f
i
∂
x
6
d
x
6
dy_i = \frac{\partial{f_i}}{\partial{x_1}}dx_1 + \frac{\partial{f_i}}{\partial{x_2}}dx_2 + \frac{\partial{f_i}}{\partial{x_3}}dx_3+ \frac{\partial{f_i}}{\partial{x_4}}dx_4+ \frac{\partial{f_i}}{\partial{x_5}}dx_5 + \frac{\partial{f_i}}{\partial{x_6}}dx_6
dyi=∂x1∂fidx1+∂x2∂fidx2+∂x3∂fidx3+∂x4∂fidx4+∂x5∂fidx5+∂x6∂fidx6
因此结合上面的方程,我们可以将上面的方程写成向量的形式:
d
Y
=
∂
F
∂
X
d
X
dY = \frac{\partial{F}}{\partial{X}}dX
dY=∂X∂FdX
在某个时间步长,雅可比矩阵其实也就是针对于
x
i
x_i
xi的函数。在下一个时间步长的时候,X已经改变了,因此雅可比矩阵也进行了改变。
雅克比矩阵与动力学
雅克比矩阵的解释
当雅可比矩阵被用在机械臂&动力学&铰链结构时,此时输入的向量
x
i
x_i
xi就变成了此时各个关节的对应值,而输出向量
y
i
y_i
yi就变成了终端关节的位置与朝向:
Y
=
[
p
x
p
y
p
z
α
x
α
y
α
z
]
T
Y=[p_x \ p_y\ p_z\ \alpha_x \ \alpha_y \ \alpha_z]^T
Y=[px py pz αx αy αz]T
针对于雅可比矩阵与机械臂的分析,在百度文库上有一篇讲述的很详细的PPT
在这种情况下,雅可比矩阵实际上真正要表述的是各个关节的角度变化率
θ
˙
θ˙
θ˙与终端关节的位置朝向
Y
˙
Y˙
Y˙的关系,这里划重点。
V
=
Y
˙
=
J
(
θ
)
θ
˙
V = \dot{Y} = J(\theta)\dot{\theta}
V=Y˙=J(θ)θ˙
向量
V
V
V就代表终端骨节的线速度和角速度,而且对应的线速度和角速度都与其当前的位置和朝向和目标位置相关。这些速度都是三维空间的,因此每个向量都有
x
,
y
,
z
x,y,z
x,y,z的元素。
V
=
[
v
x
v
y
v
z
ω
x
ω
y
ω
z
]
V = [v_x \ v_y \ v_z \ \omega_x \ \omega_y \ \omega_z ]
V=[vx vy vz ωx ωy ωz]
而
θ
˙
θ˙
θ˙指代的是各个关节的速度,在上面的方程中,是未知的。
θ
˙
=
[
θ
1
˙
θ
2
˙
.
.
.
.
θ
n
˙
]
T
\dot{\theta} = [\dot{\theta_1}\ \dot{\theta_2}\ ....\ \dot{\theta_n}\ ]^T
θ˙=[θ1˙ θ2˙ .... θn˙ ]T
J
J
J就是雅可比矩阵,指代的就是在当前的pose下,各个关节的变化导致的终端骨节的变化的矩阵。
J
=
[
∂
p
x
∂
θ
1
∂
p
x
∂
θ
2
.
.
.
∂
p
x
∂
θ
n
∂
p
y
∂
θ
1
∂
p
y
∂
θ
2
.
.
.
∂
p
y
∂
θ
n
∂
p
z
∂
θ
1
∂
p
z
∂
θ
2
.
.
.
∂
p
z
∂
θ
n
.
.
.
.
.
.
.
.
.
.
.
.
∂
α
z
∂
θ
1
∂
α
z
∂
θ
2
.
.
.
∂
α
z
∂
θ
n
]
J = \left[ \begin{matrix} \frac{\partial p_x}{\partial \theta_1} & \frac{\partial p_x}{\partial \theta_2} & ... & \frac{\partial p_x}{\partial \theta_n} \\ \frac{\partial p_y}{\partial \theta_1} & \frac{\partial p_y}{\partial \theta_2} & ... & \frac{\partial p_y}{\partial \theta_n} \\ \frac{\partial p_z}{\partial \theta_1} & \frac{\partial p_z}{\partial \theta_2} & ... & \frac{\partial p_z}{\partial \theta_n} \\ ... & ... & ... & ... \\ \frac{\partial \alpha_z}{\partial \theta_1} & \frac{\partial \alpha_z}{\partial \theta_2} & ... & \frac{\partial \alpha_z}{\partial \theta_n} \end{matrix} \right]
J=
∂θ1∂px∂θ1∂py∂θ1∂pz...∂θ1∂αz∂θ2∂px∂θ2∂py∂θ2∂pz...∂θ2∂αz...............∂θn∂px∂θn∂py∂θn∂pz...∂θn∂αz
针对于
n
n
n关节的骨骼架构,雅可比矩阵应该是
6
∗
n
6*n
6∗n的形式。
因此针对于不同的骨骼架构,雅可比矩阵的形式也不一样。例如针对铰链关节(revolute joint/ hinge joint),终端的朝向变化率基本上就是关节基于回转轴的角速度
ω
ω
ω;针对移动关节,终端关节的朝向实际上与关节的回转无关;而针对于旋转关节,终端的线速度实际上要通过旋转轴向量与关节到旋转关节的向量的叉乘来实现。
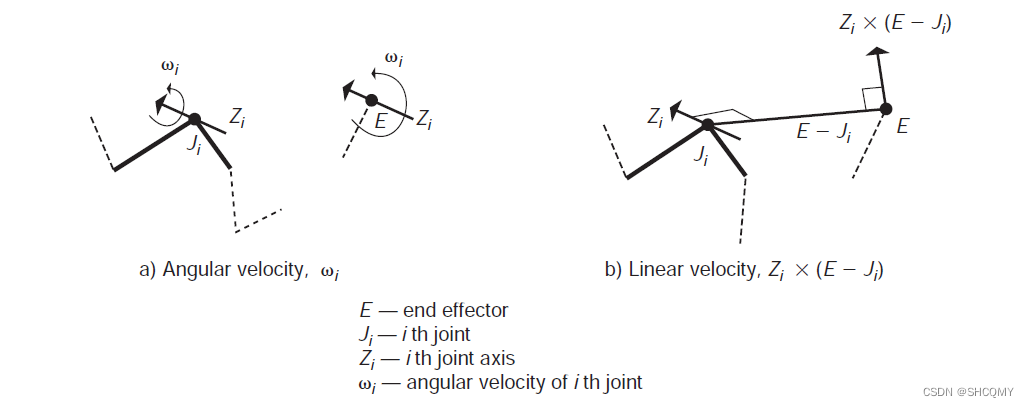
雅克比矩阵示例
考虑一个如下图的三臂铰链关节,所有的关节都约束在xy平面上,所有的约束轴向量都是(0,0,1)。
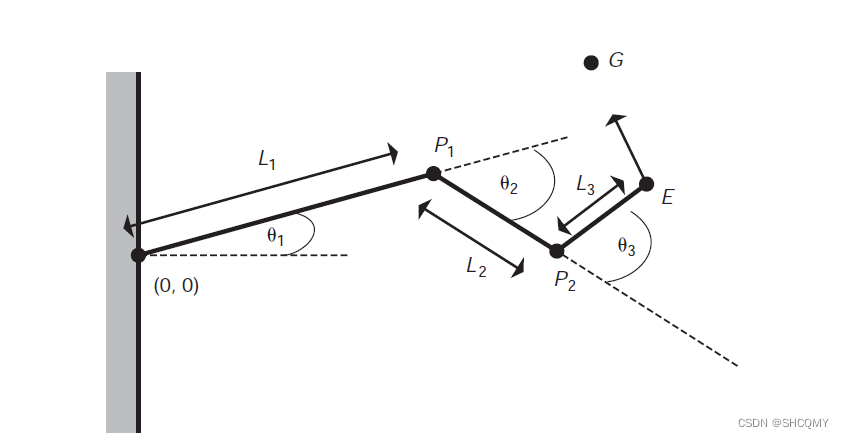
在这个示例中,终端关节
E
E
E 被尝试移动到目标位置
G
G
G,我们不考虑终端的目标的朝向应该是哪里。
由于不考虑目标的朝向应该是哪里,那么
V
V
V 向量很容易可以计算出来:
V
=
[
(
G
−
E
)
x
(
G
−
E
)
y
(
G
−
E
)
z
]
V=\left[ \begin{matrix} (G-E)_x \\ (G-E)_y \\ (G-E)_z \end{matrix} \right]
V=
(G−E)x(G−E)y(G−E)z
同样的,根据约束条件,可以很容易的计算出各个角速度:
J
=
[
(
(
0
,
0
,
1
)
×
E
)
x
(
(
0
,
0
,
1
)
×
(
E
−
P
1
)
)
x
(
(
0
,
0
,
1
)
×
(
E
−
P
2
)
)
x
(
(
0
,
0
,
1
)
×
E
)
y
(
(
0
,
0
,
1
)
×
(
E
−
P
1
)
)
y
(
(
0
,
0
,
1
)
×
(
E
−
P
2
)
)
y
(
(
0
,
0
,
1
)
×
E
)
z
(
(
0
,
0
,
1
)
×
(
E
−
P
1
)
)
z
(
(
0
,
0
,
1
)
×
(
E
−
P
2
)
)
z
]
J = \left[ \begin{matrix} ((0,0,1) \times E)_x \ \ \ ((0,0,1) \times (E-P_1))_x \ \ \ ((0,0,1) \times (E - P_2))_x \\ ((0,0,1) \times E)_y \ \ \ ((0,0,1) \times (E-P_1))_y \ \ \ ((0,0,1) \times (E - P_2))_y \\ ((0,0,1) \times E)_z \ \ \ ((0,0,1) \times (E-P_1))_z \ \ \ ((0,0,1) \times (E - P_2))_z \end{matrix} \right]
J=
((0,0,1)×E)x ((0,0,1)×(E−P1))x ((0,0,1)×(E−P2))x((0,0,1)×E)y ((0,0,1)×(E−P1))y ((0,0,1)×(E−P2))y((0,0,1)×E)z ((0,0,1)×(E−P1))z ((0,0,1)×(E−P2))z
矩阵的求解
正如之前所说,根据方程需要求得
θ
˙
θ˙
θ˙ 值的话需要求得
J
J
J 的逆矩阵:
V
=
J
θ
˙
V = J\dot{\theta}
V=Jθ˙
因此:
J
−
1
V
=
θ
˙
J^{-1}V = \dot{\theta}
J−1V=θ˙
但是就如上面所说的,通常的雅可比矩阵不一定是n*n形式的,所以此时的求解需要使用到线性代数中的广义逆(pseudoinverse)。
广义逆
矩阵的广义逆指的是在矩阵
A
A
A 不是
n
∗
n
n∗n
n∗n 形式的时候,还是有一个矩阵
A
+
A+
A+可以使得:
A
+
A
=
I
n
(
n
≤
m
)
A^+A = I_n \ \ \ \ \ \ \ (n \leq m)
A+A=In (n≤m)
或
A
A
+
=
I
m
(
m
≤
n
)
AA^+ = I_m \ \ \ \ \ \ \ (m \leq n)
AA+=Im (m≤n)
而
A
+
A^+
A+ 的值为:
A
+
=
(
A
T
A
)
−
1
A
T
(
n
≤
m
)
A^+ = (A^TA)^{-1}A^T \ \ \ \ \ \ \ (n \leq m)
A+=(ATA)−1AT (n≤m)
或
A
+
=
A
T
(
A
A
T
)
−
1
(
m
≤
n
)
A^+ = A^T(AA^T)^{-1} \ \ \ \ \ \ \ (m \leq n)
A+=AT(AAT)−1 (m≤n)
推导过程
具体的推导过程如下:
V
=
J
θ
˙
V = J\dot{\theta}
V=Jθ˙
假设此时
m
≤
n
m≤n
m≤n,那么此时有:
J
+
V
=
J
+
J
θ
˙
J^+V = J^+J\dot{\theta}
J+V=J+Jθ˙
展开
J
+
=
J
T
(
J
J
T
)
−
1
J^+ = J^T(JJ^T)^{-1}
J+=JT(JJT)−1,此时有:
J
+
V
=
J
T
(
J
J
T
)
−
1
J
θ
˙
J^+V = J^T(JJ^T)^{-1}J\dot{\theta}
J+V=JT(JJT)−1Jθ˙
将
(
J
J
T
)
−
1
(JJ^T)^{-1}
(JJT)−1 展开为
(
J
T
)
−
1
J
−
1
(J^T)^{-1}J^{-1}
(JT)−1J−1,会发现右边的公式直接被消掉,也就是说:
J
T
(
J
J
T
)
−
1
V
=
θ
˙
J^T(JJ^T)^{-1}V = \dot{\theta}
JT(JJT)−1V=θ˙
最终得到::
J
T
β
=
θ
˙
J^T\beta = \dot{\theta}
JTβ=θ˙
骨节迭代Integration
正常的Integration方法都可以用于骨骼的迭代,例如Euler Integration或者Verlet Integration等…… 但是需要注意的是,雅可比矩阵在下一个时间步长的时候已经改变了所以需要进行一次重新的计算。这个过程一直持续到终端骨节与目标位置的差值已经到了一个可以接受的误差范围为止。
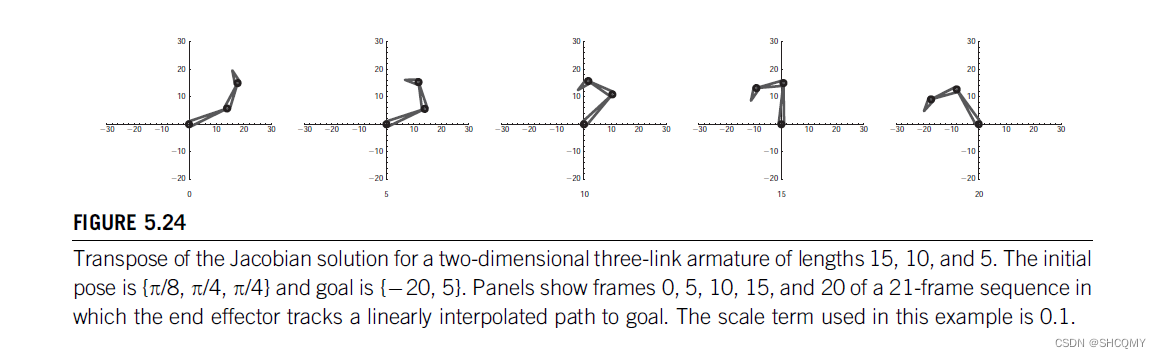
下图展示了一个臂长分别为15,10,5的机械臂。初始的pose角度分别为
π
/
8
,
π
/
4
,
π
/
4
{π/8,π/4,π/4}
π/8,π/4,π/4, 终端骨节目标点位置为
−
20
,
5
{−20,5}
−20,5。在21帧中,通过目标位置与终端骨节的线性插值方法来进行IK解算。下图显示了时间分别为0,5,15,20的情况:
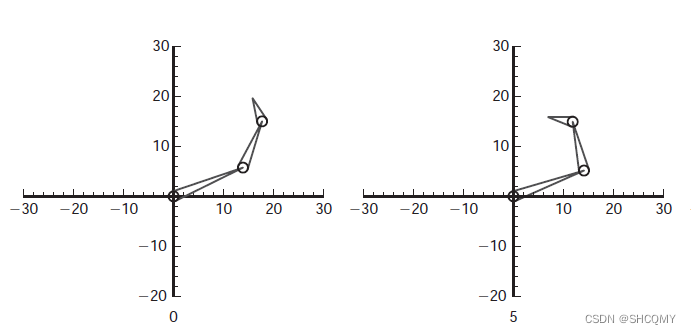
当然,需要注意的是有时矩阵依然可能会出现奇异性的状况。有人提出一种方法是使用最小二乘法来进行优化,公式如下:
θ
˙
=
J
T
(
J
J
T
+
λ
2
I
)
−
1
V
\dot{\theta} = J^T(JJ^T + \lambda^2I)^{-1}V
θ˙=JT(JJT+λ2I)−1V
但是这种方法可能会对迭代的收敛性有影响,因此这个方法到底是不是好也有争论。下图展示了是否使用最小二乘法来进行迭代结算的两种情况:
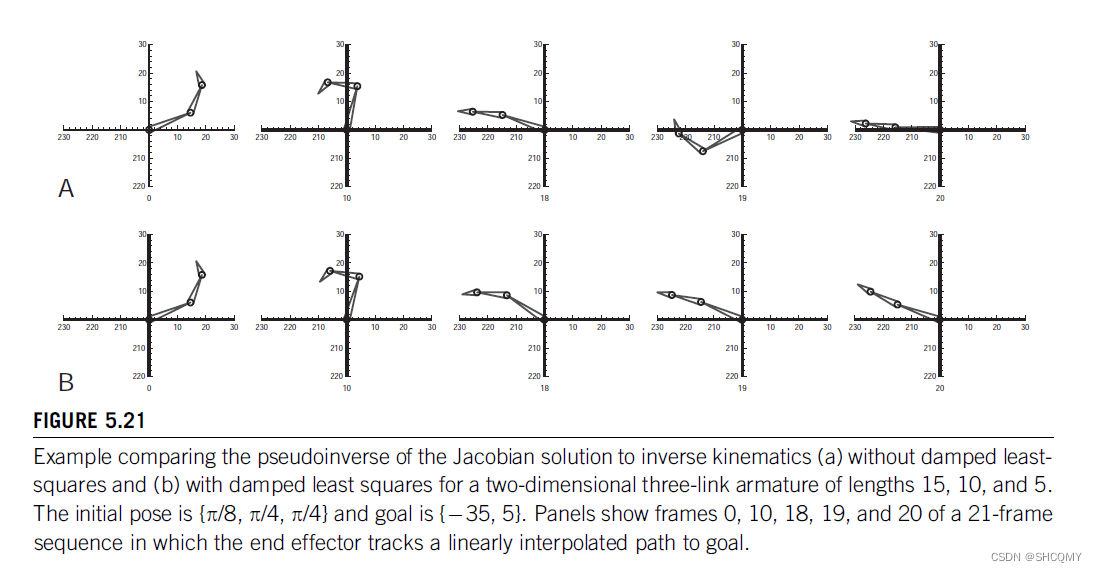
在这种情况下,目标位置是
(
−
35
,
5
)
(−35,5)
(−35,5) ,因此造成了矩阵的奇异性。因此在这个例子中使用最小二乘法能够有更好的表现。
使用雅可比矩阵的转置而不是逆
在线性代数中求逆的工作量是很大的,因此有一种可选择的方法是使用雅可比矩阵的转置而不是逆矩阵来进行结算:
θ
˙
=
α
J
T
V
\dot{\theta} = \alpha J^TV
θ˙=αJTV
这种方法可以免去求逆或广义逆的计算量,但是可能存在的风险是终端骨节可能不够稳定。
下图是使用转置矩阵的效果图:
Laplacian Mesh Editing
FABRIK
FABRIK的工作原理其实比较简单,相对于以计算效率见长的CCD来说应该还会更快一些,同时,效果也会更好。对于刚体骨骼的IK计算来说,应该是目前游戏开发这一块比较好用的IK解算算法了。
算法如下:
-
首先,针对一条从首端到尾端的bone chain,以及一个对应的Target point,先计算整条chain的长度,从而判断这个Target point是否可到达。
1.1 如果不可到达,则要求根骨骼进行移动。通常的情境类似于一个人如果伸直了手或者一只长颈鹿伸长了脖子也无法够到目标点时,则此时需要自己本身就向目标点挪(在使用Jacobian矩阵计算的环境下,此时矩阵为irregular,无对应的逆可以算出来)。
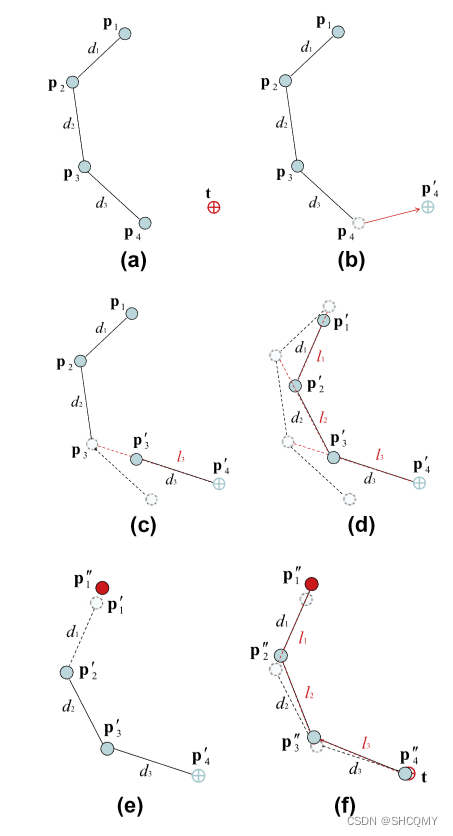
1.2 如果可以到达,那么这就意味着可以进行下一步的处理了,这里假设一共有五根骨骼(从根骨骼到末端骨骼分别是p0, p1, p2, p3, p4), 与目标位置(t)。 -
如果整条骨骼链可以保证够得着的话,那么就可以开始进行 FABRIK 的处理。整体分为两步,首先,先从末端骨骼开始计算,先将最末端的骨骼 p 4 p4 p4 移到目标位置t处,此时骨骼 p 4 p4 p4 的位置为 p ′ 4 p′4 p′4。
-
然后,将 p 3 p3 p3 和 p 4 ′ p_4^{'} p4′ 连成一条直线,通过原有的 p 3 p3 p3 和 p 4 p4 p4 的距离,将现在的 p 3 p3 p3 拉到与 p 4 ′ p_4^{'} p4′ 同样的距离处 p 3 ′ p_3^{'} p3′
-
如是者三,一直处理到根骨骼 p 0 p0 p0
-
再之后,再从根骨骼 p 0 ′ p_0^{'} p0′ 开始处理。由于根骨骼在整个迭代过程中是默认不动的,因此再把根骨骼 p 0 ′ ′ p_0^{''} p0′′ 移到原来的位置 p 0 p0 p0 处,接着使用同样的距离约束,一直处理到尾骨骼 p 4 p4 p4
-
重复2~5的迭代过程,直到最终的尾骨骼位置与到达目标位置(或与目标位置距离小于某个预定值)停止。此时整个算法结束。
过程如下图:
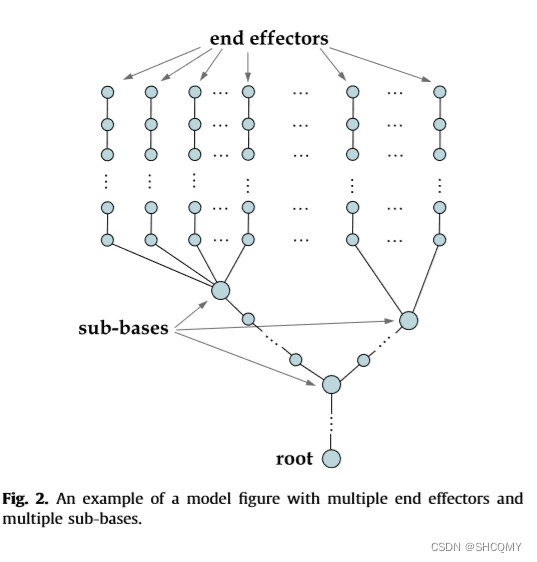
多端约束与环形约束
针对于人形骨骼(Humanoid Skeleton)来说,其实一套IK往往并不是一整根bone chain来进行结算,更多的应该是类似于bone tree(例如手掌的指头、双手同时追踪一个target)的架构。
类似的道理,FABRIK也可以使用在环形约束上。
与其他IK算法的比较
针对于普通的三角分析比较,FABRIK适用于完全未定的骨骼架构上。
针对于CCD,FABRIK可以有更好的收敛效果,甚至还可以用CGA Conformal geometric algebra进行收敛加速。
针对于雅可比矩阵操作,FABRIK最终产生的效果不一定比雅可比矩阵更好,但是计算量大大减少。
