[蓝桥杯 2021 省 A] 填空问题

试题 A：卡片

小蓝有很多数字卡片，每张卡片上都是数字 $0$ 到 $9$ 。

小蓝准备用这些卡片来拼一些数，他想从 $1$ 开始拼出正整数，每拼一个，就保存起来，卡片就不能用来拼其它数了。

小蓝想知道自己能从 $1$ 拼到多少。

例如，当小蓝有 $30$ 张卡片，其中 $0$ 到 $9$ 各 $3$ 张，则小蓝可以拼出 $1$ 到 $10$ ，但是拼 $11$ 时卡片 $1$ 已经只有一张了，不够拼出 $11$ 。

现在小蓝手里有 $0$ 到 $9$ 的卡片各 $2021$ 张，共 $20210$ 张，请问小蓝可以从 $1$ 拼到多少?
思路

• 模拟+枚举即可，简单

3181

试题 B：直线

【问题描述】

在平面直角坐标系中，两点可以确定一条直线。如果有多点在一条直线上，那么这些点中任意两点确定的直线是同一条。

给定平面上 $2\times 3$ 个整点 $\{(x,y)\mid 0\le x<2,0\le y<3,x\in \mathbb{Z},y\in \mathbb{Z}\}$，即横坐标是 $0$ 到 $1$ (包含 $0$ 和 $1$ ) 之间的整数、纵坐标是 $0$ 到 $2$ (包含 $0$ 和 $2$ ) 之间的整数的点。这些点一共确定了 $11$ 条不同的直线。

给定平面上 $20\times 21$ 个整点 $\{(x,y)\mid 0\le x<20,0\le y<21,x\in \mathbb{Z},y\in \mathbb{Z}\}$，即横坐标是 $0$ 到 $19$ (包含 $0$ 和 $19$ ) 之间的整数、纵坐标是 $0$ 到 $20$ (包含 $0$ 和 $20$ ) 之间的整数的点。请问这些点一共确定了多少条不同的直线。

思路

• 想到用线性方程组来判重，但是觉得会出现浮点数影响判断
• 别人的思路：用线性方程组判重

试题 C ：货物摆放

【问题描述】

小蓝有一个超大的仓库，可以摆放很多货物。

现在，小蓝有 $n$ 箱货物要摆放在仓库，每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向，每箱货物的边都必须严格平行于长、 宽、高。

小蓝希望所有的货物最终摆成一个大的立方体。即在长、宽、高的方向上分别堆 $L、W、H$ 的货物，满足 $n=L\times W\times H$。

给定 $n$，请问有多少种堆放货物的方案满足要求。

例如，当 $n=4$ 时，有以下 $6$ 种方案：$1\times 1\times 4、1\times 2\times 2、1\times 4\times 1、2\times 1\times 2$ 、 $2\times 2\times 1、4\times 1\times 1$

请问，当 $n=2021041820210418$ (注意有 $16$ 位数字) 时，总共有多少种方案?

思路

• 我想的就是简单粗暴的遍历，$O(n^3)$并且$n=2021041820210418$，应该是做不了的
• 别人的解法：找因数

试题 D：路径

【问题描述】

小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图中的最短路径。

小蓝的图由 $2021$ 个结点组成，依次编号 $1$ 至 $2021$ 。

对于两个不同的结点 $a,b$，如果 $a$ 和 $b$ 的差的绝对值大于 $21$ ，则两个结点之间没有边相连; 如果 $a$ 和 $b$ 的差的绝对值小于等于 $21$ ，则两个点之间有一条长度为 $a$ 和 $b$ 的最小公倍数的无向边相连。

例如：结点 $1$ 和结点 $23$ 之间没有边相连; 结点 $3$ 和结点 $24$ 之间有一条无向边，长度为 $24$ ; 结点 $15$ 和结点 $25$ 之间有一条无向边，长度为 $75$ 。

请计算，结点 $1$ 和结点 $2021$ 之间的最短路径长度是多少。

思路

• 用最大公因数gcd算出最小公倍数赋值给边权，然后用$Dijstra$算法计算源点最短路径

试题 E：回路计数

【问题描述】

蓝桥学院由 $21$ 栋教学楼组成，教学楼编号 $1$ 到 $21$ 。对于两栋教学楼 $a$ 和 $b$，当 $a$ 和 $b$ 互质时，$a$ 和 $b$ 之间有一条走廊直接相连，两个方向皆可通行，否则没有直接连接的走廊。

小蓝现在在第一栋教学楼，他想要访问每栋教学楼正好一次，最终回到第一栋教学楼（即走一条哈密尔顿回路)，请问他有多少种不同的访问方案? 两个访问方案不同是指存在某个 $i$，小蓝在两个访问方法中访问完教学楼 $i$ 后访问了不同的教学楼。

思路

• 数论+动态规划
• 状压dp

编程题

[蓝桥杯 2021 省 AB] 砝码称重

• 做过

[蓝桥杯 2021 省 A] 异或数列

• 做过

[蓝桥杯 2021 省 A] 左孩子右兄弟

对于一棵多叉树，我们可以通过“左孩子右兄弟”表示法，将其转化成一棵二叉树。

如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。

给定一棵包含 $N$ 个结点的多叉树，结点从 $1$ 至 $N$ 编号，其中 $1$ 号结点是根，每个结点的父结点的编号比自己的编号小。请你计算其通过"左孩子右兄弟"表示法转化成的二叉树，高度最高是多少。（只有根结点这一个结点的树高度为 $0$）

例如如下的多叉树：

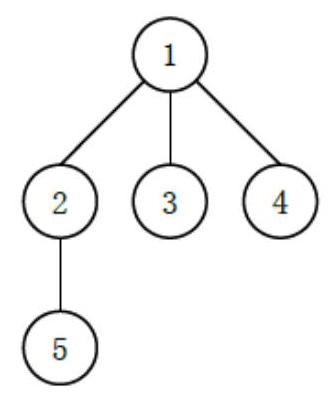
可能有以下 $3$ 种 (这里只列出 $3$ 种, 并不是全部) 不同的 “左孩子右兄弟” 表示:

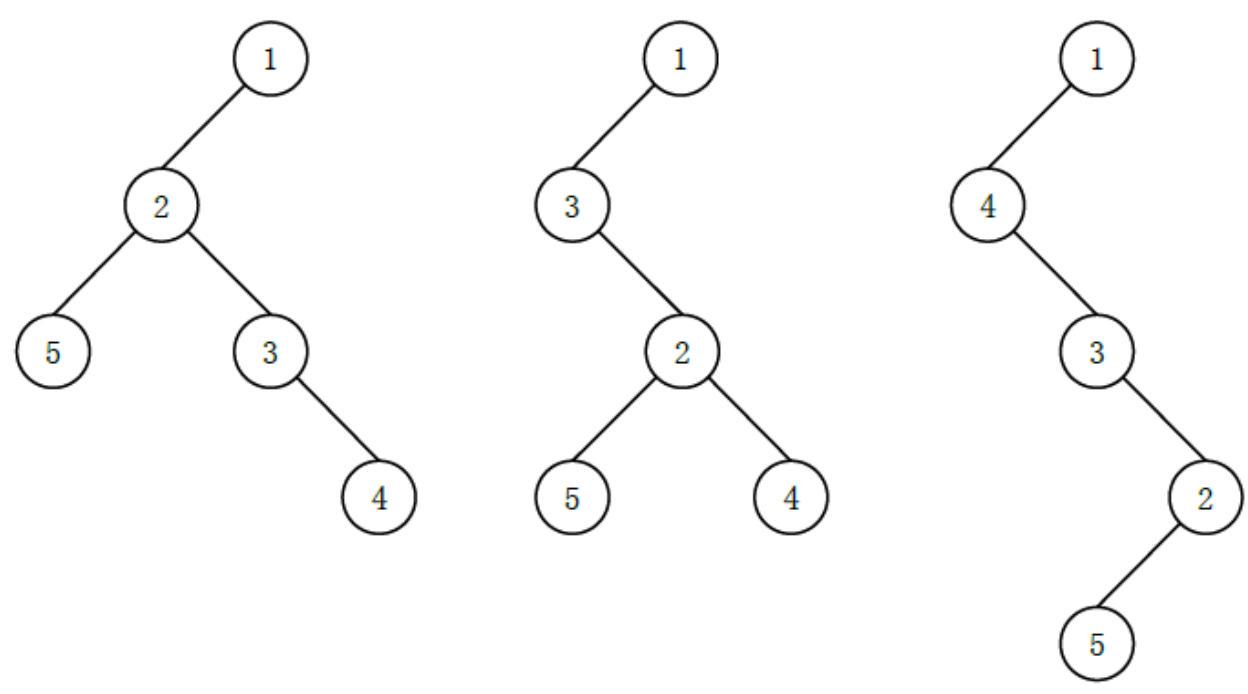
其中最后一种高度最高, 为 $4$。

输入格式

输入的第一行包含一个整数 $N$ 。

以下 $N-1$ 行, 每行包含一个整数, 依次表示 $2$ 至 $N$ 号结点的父结点编号。

输出格式

输出一个整数表示答案。

样例输入 #1

5
1
1
1
2

样例输出 #1

4

提示

对于 $30\%$ 的评测用例，$1\le N\le 20$;

对于所有评测用例，$1\le N\le 10^5$ 。

蓝桥杯 2021 第一轮省赛 A 组 H 题。

思路

• 动态规划，状态：$f[i]$表示$i$之后的最长子树高度，状态转移：$f[i]=max(f[i_{son}])+i_{son}.size$。
• 用$dfs$找出$f[i_{son}]$

题解

#include<bits/stdc++.h>
using namespace std;
long long n,x,f[100005];
vector<long long>v[100005]; 
void dfs(long long x){
	for(auto i:v[x]){
		dfs(i);
		f[x]=max(f[x],f[i]);
	}
	f[x]+=v[x].size();
} 
int main(){
	scanf("%lld",&n);
	for(int i=2;i<=n;i++){
		scanf("%lld",&x);
		v[x].push_back(i);
	}
	dfs(1); 
	cout<<f[1]<<endl; 
}