当前位置：首页 > article >正文

61-二分搜索树BST

article 2024/11/17 13:40:08

目录

1.概念

2.操作

2.1.插入add

2.2.查找contains/maximum/minimum

2.2.1.查找BST中是否包含指定值->二分查找boolean contains(int val)

2.2.2.返回BST的最大值int maximum()

2.2.3.返回BST的最小值int minimum()

2.3.删除

2.3.1.删除最大值

2.3.2.删除最小值

2.3.3.删除任意元素

3.方法实现

3.1.向BST中添加一个新元素，用户使用

3.2.向以root为根节点的BST中添加一个新元素value

3.3.判断以root为根节点的BST中是否包含指定元素val，用户使用

3.4.判断以root为根节点的BST中是否包含指定元素val

3.5.找到当前以root为根节点的BST中的最大值节点，用户使用

3.6.找到当前以root为根节点的BST中的最大值节点

3.7.找到当前以root为根节点的BST中的最小值节点，用户使用

3.8.找到当前以root为根节点的BST中的最小值节点

3.9.删除最小值节点，返回最小值，用户使用

3.10.删除以当前root为根节点的BST中的最小值节点

3.11.删除最大值节点，返回最大值，用户使用

3.12.删除以当前root为根节点的BST中的最大值节点

3.13.在以root为根节点的二叉树中，删除值为val的节点，用户使用

3.14.在以root为根节点的二叉树中，删除值为val的节点

3.15.先序遍历二分搜索树

3.16.打印当前BST的深度，每进入下一层就多两个--

3.17.toString方法

4.总代码实现

5.测试实现

6.性能分析

JDK底层的Map有2种结构：

二分搜素树
哈希表

1.概念

二分搜索树（BST-Binary Search Tree），又称二叉搜索树、二叉排序树，它要么是一棵空树，要么是具有以下性质的二叉树：

是棵二叉树（没有要求平衡性）。
节点值：左孩子<根节点<右孩子，递归定义，BST中序遍历是一个升序集合，JDK的BST不存在重复元素。
存储的元素必须具备可比较性（自定义的类实现Comparable或者传入比较器Comparator）。
关于最值问题：

最小值：第一个node.left == null的节点。
最大值：第一个node.right == null的节点。

它的左右子树也分别为二叉搜索树。

2.操作

BST中每个操作都对应2个方法：一个public，用户使用；一个private，内部调用递归实现，对外界不可见。

2.1.插入add

向BST中添加一个元素，一定是添加到叶子节点，此处我们定义的BST不存在重复元素。

2.2.查找contains/maximum/minimum

2.2.1.查找BST中是否包含指定值->二分查找boolean contains(int val)

2.2.2.返回BST的最大值int maximum()

最大值一定出现在右树，一路向右。即为一直向右子树查找过程中碰到的第一个node.right == null，node即为所求。

2.2.3.返回BST的最小值int minimum()

最小值一定出现在左树，一路向左。即为一直向左子树查找过程中碰到的第一个node.left == null，node即为所求。

注：maximum和minimum的遍历是单支树遍历，不算二分查找，遍历过程就是之前的链表遍历。

2.3.删除

2.3.1.删除最大值

最大值的右孩子一定为空，只需要将左子树连接即可。

2.3.2.删除最小值

最小值的左孩子一定为空，只需要将右子树连接即可。

2.3.3.删除任意元素

3.方法实现

3.1.向BST中添加一个新元素，用户使用

/**
 * 向BST中添加一个新元素,用户使用
 * @param value
 */
public void add(int value) {
    root = add(root,value);
}

3.2.向以root为根节点的BST中添加一个新元素value

/**
 * 向以root为根节点的BST中添加一个新元素value
 * @param root
 * @param value
 * @return 返回添加元素后的根节点
 */
private Node add(Node root, int value) {
    //当root为空时，此时走到叶子节点，创建新节点插入值
    if(root == null) {
        root = new Node(value);
        size++;
        return root;
    }
    //此时还没走到根节点，需要比较value和根节点值的大小关系
    if(value < root.val) {
        //在左树中添加
        root.left = add(root.left, value);
        return root;
    }
    //在右树中添加
    root.right = add(root.right, value);
    return root;
}

3.3.判断以root为根节点的BST中是否包含指定元素val，用户使用

/**
 * 判断以root为根节点的BST中是否包含指定元素val,用户使用
 * @param val
 * @return
 */
public boolean contains(int val) {
    return contains(root, val);
}

3.4.判断以root为根节点的BST中是否包含指定元素val

/**
 * 判断以root为根节点的BST中是否包含指定元素val
 * @param root
 * @param val
 * @return
 */
private boolean contains(Node root, int val) {
    if(root == null) {
        return false;
    }
    //根节点恰好就是待查找到的值
    else if(root.val == val) return true;
    //左树中找
    else if(val < root.val) return contains(root.left, val);
    //右树中找
    return contains(root.right, val);
}

3.5.找到当前以root为根节点的BST中的最大值节点，用户使用

/**
 * 找到当前以root为根节点的BST中的最大值节点,用户使用
 * @return
 */
public int maximum() {
    if(size == 0) {
        throw new NoSuchElementException("bst is empty!");
    }
    //找到最大值所在的节点
    Node maxNode = maximum(root);
    return maxNode.val;
}

3.6.找到当前以root为根节点的BST中的最大值节点

/**
 * 找到当前以root为根节点的BST中的最大值节点
 * @param root
 * @return
 */
private Node maximum(Node root) {
    if(root.right == null) {
        //此时右孩子为空，则root就是最大值节点
        return root;
    }
    return maximum(root.right);
}

3.7.找到当前以root为根节点的BST中的最小值节点，用户使用

/**
 * 找到当前以root为根节点的BST中的最小值节点,用户使用
 * @return
 */
public int minimum() {
    if(size == 0) {
        throw new NoSuchElementException("bst is empty!");
    }
    //找到最小值所在的节点
    Node minNode = minimum(root);
    return minNode.val;
}

3.8.找到当前以root为根节点的BST中的最小值节点

/**
 * 找到当前以root为根节点的BST中的最小值节点
 * @param root
 * @return
 */
private Node minimum(Node root) {
    if(root.left == null) {
        //此时左孩子为空，则root就是最大值节点
        return root;
    }
    return minimum(root.left);
}

3.9.删除最小值节点，返回最小值，用户使用

/**
 * 删除最小值节点，返回最小值，用户使用
 * @return
 */
public int removeMin() {
    int min = minimum();
    root = removeMin(root);
    return min;
}

3.10.删除以当前root为根节点的BST中的最小值节点

/**
 * 删除以当前root为根节点的BST中的最小值节点
 * @param root
 * @return 返回删除后的根节点
 */
private Node removeMin(Node root) {
    if(root.left == null) {
        //此时root为最小值节点
        //将右树返回
        Node right = root.right;
        //断支 等同于 链表删除时，node.next = null;
        root.right = null;
        size--;
        return right;
    }
    root.left = removeMin(root.left);
    return root;
}

3.11.删除最大值节点，返回最大值，用户使用

/**
 * 删除最大值节点，返回最大值，用户使用
 * @return
 */
public int removeMax() {
    int max = maximum();
    root = removeMax(root);
    return max;
}

3.12.删除以当前root为根节点的BST中的最大值节点

/**
 * 删除以当前root为根节点的BST中的最大值节点
 * @param root
 * @return 返回删除后的根节点
 */
private Node removeMax(Node root) {
    if(root.right == null) {
        //此时root为最大值节点
        //将左树返回
        Node left = root.left;
        //断支 等同于 链表删除时，node.next = null;
        root.left = null;
        size--;
        return left;
    }
    root.right = removeMax(root.right);
    return root;
}

3.13.在以root为根节点的二叉树中，删除值为val的节点，用户使用

/**
 * 在以root为根节点的二叉树中，删除值为val的节点，用户使用
 * @param val
 */
public void remove(int val) {
    root = remove(root, val);
}

3.14.在以root为根节点的二叉树中，删除值为val的节点

/**
 * Hibbard Deletion
 * 在以root为根节点的二叉树中，删除值为val的节点
 * @param root
 * @param val
 * @return 返回删除后的根节点
 */
private Node remove(Node root, int val) {
    if(root == null) {
        //都把BST遍历完了，也没找到值为val的节点
        return null;
    } else if(val < root.val) {
        //在左树删除
        root.left = remove(root.left, val);
        return root;
    } else if(val > root.val) {
        //在右树删除
        root.right = remove(root.right, val);
        return root;
    } else {
        //此时root就是待删除的节点
        if(root.left == null) {
            //只有右孩子，返回右孩子即可
            Node right = root.right;
            root.right = null;
            size--;
            return right;
        }
        if(root.right == null) {
            //只有左孩子，返回左孩子即可
            Node left = root.left;
            root.left = null;
            size--;
            return left;
        }
        //此时说明root.left != null && root.right != null
        //找到root的后继节点
        Node successor = minimum(root.right);
        //在右子树中删除最小值，连接为successor的右子树
        //在右子树删除后继节点的时候已经size--了
        //此时是把root替换为successor,因此size不用再--
        successor.right = removeMin(root.right);
        //连接root的左子树为successor的左子树
        successor.left = root.left;
        root.left = root.right = null;
        //此处为何没有size--?
        //在右子树删除后继节点的时候已经size--了
        //此时是把root替换为successor,因此size不用再--
        return successor;
    }
}

3.15.先序遍历二分搜索树

/**
 * 先序遍历二分搜索树
 * @param root BST的根节点
 * @param depth 当前树的深度
 * @param sb
 */
private void generateBSTString(Node root, int depth, StringBuilder sb) {
    if(root == null) {
        sb.append(generateBSTDepth(depth)).append("NULL\n");
        return;
    }
    //先根节点
    sb.append(generateBSTDepth(depth)).append(root.val + "\n");
    //递归访问左子树
    generateBSTString(root.left, depth + 1, sb);
    //递归访问右子树
    generateBSTString(root.right, depth + 1, sb);
}

3.16.打印当前BST的深度，每进入下一层就多两个--

/**
 * 打印当前BST的深度，每进入下一层就多两个--
 * @param depth
 * @return
 */
private String generateBSTDepth(int depth) {
    StringBuilder sb = new StringBuilder();
    for (int i = 0; i < depth; i++) {
        sb.append("--");
    }
    return sb.toString();
}

3.17.toString方法

@Override
public String toString() {
   StringBuilder sb = new StringBuilder();
   generateBSTString(root,0,sb);
   return sb.toString();
}

4.总代码实现

import java.util.NoSuchElementException;

/**
 * 基于int的二分搜索树，不包含重复元素
 */
public class BST {
    //节点个数
    private int size;
    //根节点
    private Node root;

    //节点定义
    private class Node {
        private int val;
        private Node left;
        private Node right;

        public Node(int val) {
            this.val = val;
        }
    }

    /**
     * 向BST中添加一个新元素,用户使用
     * @param value
     */
    public void add(int value) {
        root = add(root,value);
    }

    /**
     * 向以root为根节点的BST中添加一个新元素value
     * @param root
     * @param value
     * @return 返回添加元素后的根节点
     */
    private Node add(Node root, int value) {
        //当root为空时，此时走到叶子节点，创建新节点插入值
        if(root == null) {
            root = new Node(value);
            size++;
            return root;
        }
        //此时还没走到根节点，需要比较value和根节点值的大小关系
        if(value < root.val) {
            //在左树中添加
            root.left = add(root.left, value);
            return root;
        }
        //在右树中添加
        root.right = add(root.right, value);
        return root;
    }

    /**
     * 判断以root为根节点的BST中是否包含指定元素val,用户使用
     * @param val
     * @return
     */
    public boolean contains(int val) {
        return contains(root, val);
    }

    /**
     * 判断以root为根节点的BST中是否包含指定元素val
     * @param root
     * @param val
     * @return
     */
    private boolean contains(Node root, int val) {
        if(root == null) {
            return false;
        }
        //根节点恰好就是待查找到的值
        else if(root.val == val) return true;
        //左树中找
        else if(val < root.val) return contains(root.left, val);
        //右树中找
        return contains(root.right, val);
    }

    /**
     * 找到当前以root为根节点的BST中的最大值节点,用户使用
     * @return
     */
    public int maximum() {
        if(size == 0) {
            throw new NoSuchElementException("bst is empty!");
        }
        //找到最大值所在的节点
        Node maxNode = maximum(root);
        return maxNode.val;
    }

    /**
     * 找到当前以root为根节点的BST中的最大值节点
     * @param root
     * @return
     */
    private Node maximum(Node root) {
        if(root.right == null) {
            //此时右孩子为空，则root就是最大值节点
            return root;
        }
        return maximum(root.right);
    }

    /**
     * 找到当前以root为根节点的BST中的最小值节点,用户使用
     * @return
     */
    public int minimum() {
        if(size == 0) {
            throw new NoSuchElementException("bst is empty!");
        }
        //找到最小值所在的节点
        Node minNode = minimum(root);
        return minNode.val;
    }

    /**
     * 找到当前以root为根节点的BST中的最小值节点
     * @param root
     * @return
     */
    private Node minimum(Node root) {
        if(root.left == null) {
            //此时左孩子为空，则root就是最大值节点
            return root;
        }
        return minimum(root.left);
    }

    /**
     * 删除最小值节点，返回最小值，用户使用
     * @return
     */
    public int removeMin() {
        int min = minimum();
        root = removeMin(root);
        return min;
    }

    /**
     * 删除以当前root为根节点的BST中的最小值节点
     * @param root
     * @return 返回删除后的根节点
     */
    private Node removeMin(Node root) {
        if(root.left == null) {
            //此时root为最小值节点
            //将右树返回
            Node right = root.right;
            //断支 等同于 链表删除时，node.next = null;
            root.right = null;
            size--;
            return right;
        }
        root.left = removeMin(root.left);
        return root;
    }

    /**
     * 删除最大值节点，返回最大值，用户使用
     * @return
     */
    public int removeMax() {
        int max = maximum();
        root = removeMax(root);
        return max;
    }

    /**
     * 删除以当前root为根节点的BST中的最大值节点
     * @param root
     * @return 返回删除后的根节点
     */
    private Node removeMax(Node root) {
        if(root.right == null) {
            //此时root为最大值节点
            //将左树返回
            Node left = root.left;
            //断支 等同于 链表删除时，node.next = null;
            root.left = null;
            size--;
            return left;
        }
        root.right = removeMax(root.right);
        return root;
    }

    /**
     * 在以root为根节点的二叉树中，删除值为val的节点，用户使用
     * @param val
     */
    public void remove(int val) {
        root = remove(root, val);
    }

    /**
     * Hibbard Deletion
     * 在以root为根节点的二叉树中，删除值为val的节点
     * @param root
     * @param val
     * @return 返回删除后的根节点
     */
    private Node remove(Node root, int val) {
        if(root == null) {
            //都把BST遍历完了，也没找到值为val的节点
            return null;
        } else if(val < root.val) {
            //在左树删除
            root.left = remove(root.left, val);
            return root;
        } else if(val > root.val) {
            //在右树删除
            root.right = remove(root.right, val);
            return root;
        } else {
            //此时root就是待删除的节点
            if(root.left == null) {
                //只有右孩子，返回右孩子即可
                Node right = root.right;
                root.right = null;
                size--;
                return right;
            }
            if(root.right == null) {
                //只有左孩子，返回左孩子即可
                Node left = root.left;
                root.left = null;
                size--;
                return left;
            }
            //此时说明root.left != null && root.right != null
            //找到root的后继节点
            Node successor = minimum(root.right);
            //在右子树中删除最小值，连接为successor的右子树
            //在右子树删除后继节点的时候已经size--了
            //此时是把root替换为successor,因此size不用再--
            successor.right = removeMin(root.right);
            //连接root的左子树为successor的左子树
            successor.left = root.left;
            root.left = root.right = null;
            //此处为何没有size--?
            //在右子树删除后继节点的时候已经size--了
            //此时是把root替换为successor,因此size不用再--
            return successor;
        }
    }

    /**
     * 先序遍历二分搜索树
     * @param root BST的根节点
     * @param depth 当前树的深度
     * @param sb
     */
    private void generateBSTString(Node root, int depth, StringBuilder sb) {
        if(root == null) {
            sb.append(generateBSTDepth(depth)).append("NULL\n");
            return;
        }
        //先根节点
        sb.append(generateBSTDepth(depth)).append(root.val + "\n");
        //递归访问左子树
        generateBSTString(root.left, depth + 1, sb);
        //递归访问右子树
        generateBSTString(root.right, depth + 1, sb);
    }

    /**
     * 打印当前BST的深度，每进入下一层就多两个--
     * @param depth
     * @return
     */
    private String generateBSTDepth(int depth) {
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < depth; i++) {
            sb.append("--");
        }
        return sb.toString();
    }

    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        generateBSTString(root,0,sb);
        return sb.toString();
    }
}

5.测试实现

public class BSTTest {
    public static void main(String[] args) {
        BST bst = new BST();
        int[] data = {41,58,50,60,42,53,59,63};
        for (int i = 0; i < data.length; i++) {
            bst.add(data[i]);
        }
        bst.add(35);
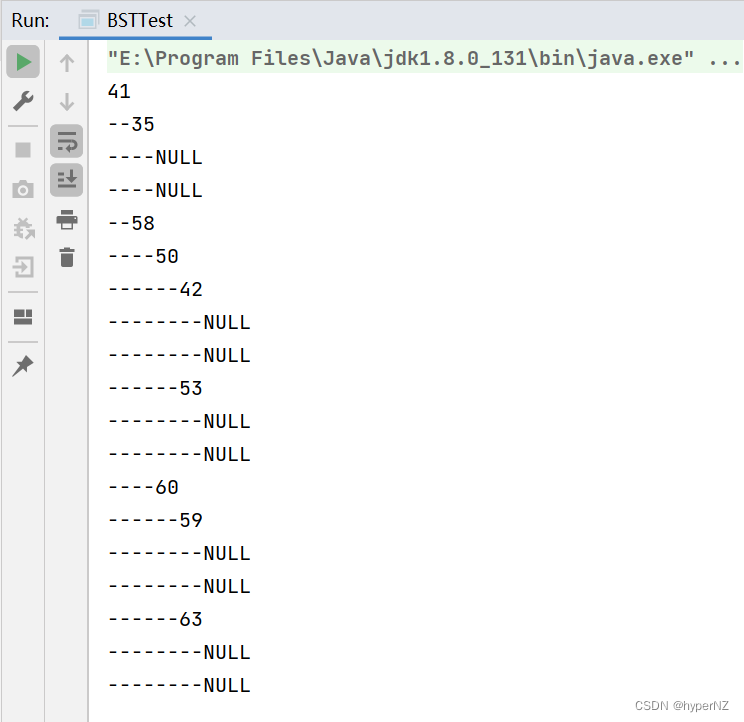
        System.out.println(bst);
        System.out.println(bst.contains(29));
        System.out.println(bst.contains(13));
        System.out.println(bst.contains(100));
        System.out.println(bst.maximum());
        System.out.println(bst.minimum());
        System.out.println("最小值:" + bst.removeMin());
        System.out.println(bst);
        System.out.println("最大值:" + bst.removeMax());
        bst.remove(58);
        System.out.println(bst);
    }
}

6.性能分析

看到二分搜索树，天然的查找语义=>查找过程中使用二分法。
插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。
对有n个节点的二叉搜索树，若每个元素查找的概率相同，则二叉搜索树平均查找长度是节点在二叉树的深度的函数，即节点越深，比较次数越多。
对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树。

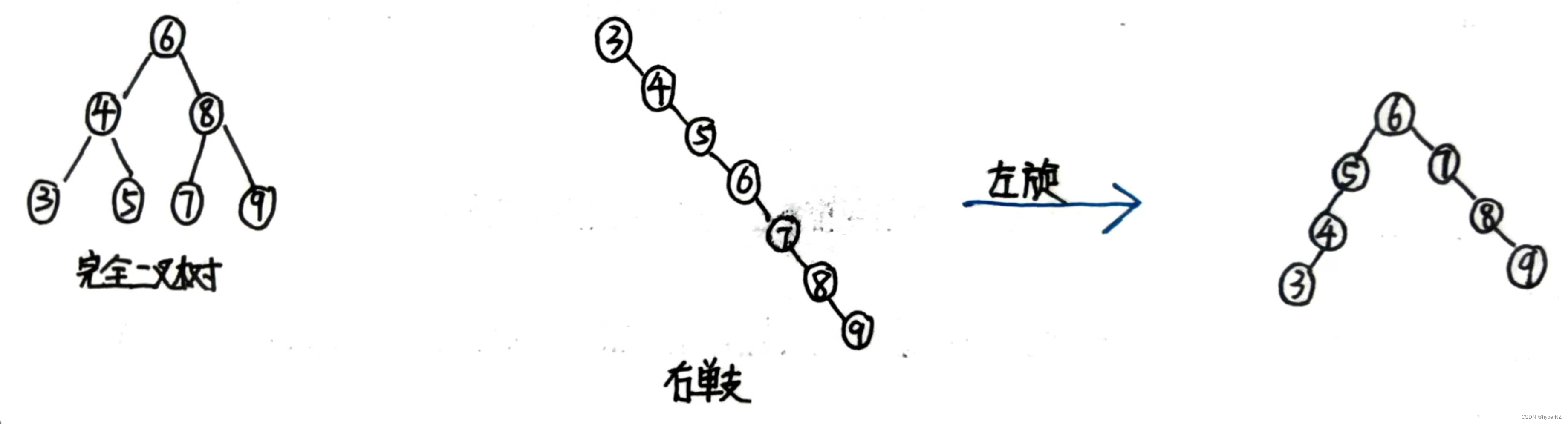
最优情况下：二叉搜索树为完全二叉树，其平均比较次数为log2N。
最差情况下：二叉搜索树退化为单支树（链表），其平均查找次数为N/2。插入、删除、查找操作都变为了链表的遍历过程，时间复杂度O(N)，原先是O(logN)。

改进：正因为节点值若接近于有序，BST会退化为单支树或者高度严重不平衡的树，故引入二分平衡树AVL，红黑树，添加时会进行节点的旋转。

红黑树：是一棵近似平衡的二叉搜索树，即在二叉搜索树的基础上+颜色以及红黑树性质验证，TreeMap和TreeSet即Java中利用搜索树实现的Map和Set，实际上用的是红黑树。

http://www.kler.cn/a/7528.html

相关文章：

查询DBA_FREE_SPACE缓慢问题

Nginx 上安装 SSL 证书并启用 HTTPS 访问

企业生产环境-麒麟V10（ARM架构）操作系统部署kafka高可用集群

Unity类银河战士恶魔城学习总结（P127 Stat ToolTip属性提示）

uview Collapse折叠面板无法动态设置展开问题（微信小程序）

计算机视觉 ---常见图像文件格式及其特点

为什么我们认为GPT是一个技术爆炸

面试腾讯T7，被按在地上摩擦，鬼知道我经历了什么？

常用设计模式(超级无敌认真好用，万字收藏篇!!!!)

【Redis学习】Redis复制(replica)

算法自学__线性动态规划

Word控件Spire.Doc 【页眉页脚】教程(10)：锁定标题以防止在 C# 中编辑 word 文档

Python 异常处理

【电商干货】旺旺满意度考核你达标了吗？

ChatGPT 辅助软件编程

Autosar COM Stack系列介绍01_一文看懂各层PDU

Java重写(Override)重载(Overload)

shiro漏洞复现及其攻击流量分析

【Nowcoder-BC146.添加逗号 -OR63.删除公共字符】

【蓝桥杯】【省赛真题】

类方法与类变量与main方法语法

有哪些 python 的在线练习题或编程挑战的网站？

4.6---Spring框架之Spring的AOP理解(复习版本）

一致性哈希的简单认识

蓝牙耳机品牌哪个音质好佩戴舒适性？2023年蓝牙耳机盘点

【Redis】数据结构 - Set