实现 GPS 拒绝飞机导航的时间序列模型(Matlab代码实现)
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
👨💻4 Matlab代码
💥1 概述
该项目旨在开发一个时间序列预测模型,以解决GPS拒绝飞机导航的问题,这是空中交通管制的关键要素。该项目实现了两种不同的时间序列模型,即ARIMA和LSTM。这些模型将用于在线预测飞机接下来 100 个时间步的纬度、经度和高度。仿真结果表明,所建立的模型能够以较高的置信区间准确预测飞机位置。
通常时间序列是某一系统在不同时刻的数值组成的数列,由按时间先后顺序排列的一连串的观测数据(信号)组成的数列,按规定的时间间隔采样,因为采样时的条件不可能完全一样,所以往往会表现出随机性,时间序列的未来取值呈现出不可预测性,同时期的前后观测值之间也存在一定的相关性。
a.趋势变化,是指时间序列随着时间的变化,表现出上升或降低的长期趋势。
b.季节性变化,通常是指时间序列包含的一些周期性项,如周年、半周年、季节性变化等。
c.循环变化,主要是指趋势线在较长时间里表现出来的上下波动的现象。
d.不规则变化,又称不规则因子,反映了系统受随机性事件而引起的在间断点处的变化(如地震引起的垂直位移)。
📚2 运行结果
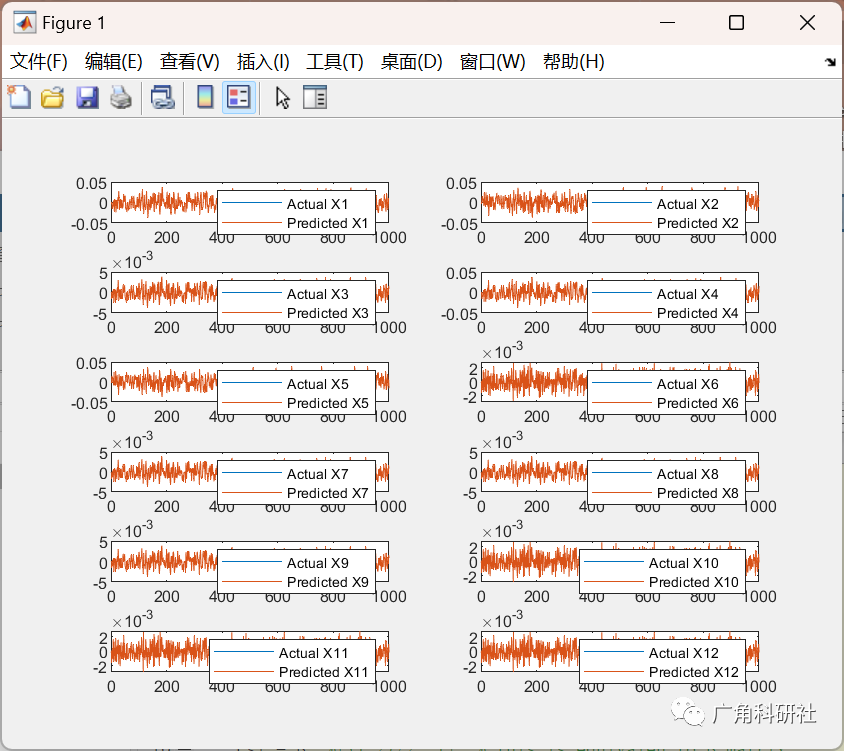

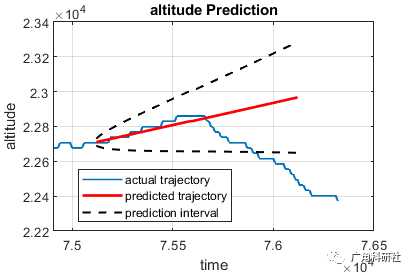

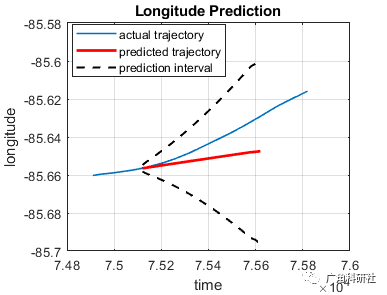
主函数部分代码:
clc; clear all; close all;
% Given parameters
T = 0.01;
Phi = [1 T;0 1]; % this is equivalent to A matrix
Psi = [(T^2)/2; T]; % this is equivalen to B matrix
H = [1 0]; % this is equivalent to C matrix
Gamma = [(T^2)/2 0;T 0.01]; % this is equivalent to W
Gam = [0;0.01]; % this is only for W in the dynamical system
Q = 0.001;%*eye(2);
R = 0.1;%*eye(2);
u_variance = 0.1;
u_meanValue = 0;
w_variance = 0.001;
w_meanValue = 0;
v_variance = 0.1;
v_meanValue = 0;
% Implementation of kalman filter for the above system
K = [];
P = []; % The filter error covariance
P_int = []; % P(k+1|k) -- Error covariance of the prediction x(k+1|k)
X = [];
X_hat = [];
Z_hat = [];
X_predict = [];
P(:,:,1) = 0.1*eye(2);
X_hat(:,:,1) = zeros(2,1);
X_predict(:,:,1) = zeros(2,1);
X(:,:,1) = [0;0];
for k = 1:1000
% First construct the kalman gain matrix [K(k+1)]
P_int(:,:,k) = Phi*P(:,:,k)*Phi' + Gamma*Q*Gamma'; % this is line 2 of section B
K(:,:,k+1) = P_int(:,:,k)*(H')*inv(H*P_int(:,:,k)*H' + R); % This is line 1 of section B
P(:,:,k+1) = (eye(2) - K(:,:,k+1)*H)*P_int(:,:,k); % This is line 3 of section B
% Now let's implement the Kalman filter -- section 1
% First let's implement the system to get Z(k+1)
%%%%%%%%%%%%
u_wnoise = sqrt(u_variance)*randn(size(1)) + u_meanValue;
w_wnoise = sqrt(w_variance)*randn(size(1)) + w_meanValue;
v_wnoise = sqrt(v_variance)*randn(size(1)) + v_meanValue;
X(:,:,k+1) = Phi*X(:,:,k) + Psi*u_wnoise + Gam*w_wnoise;
Z(:,:,k+1) = H*X(:,:,k+1) +v_wnoise;
%%%%%%%%%%%%
X_predict(:,:,k) = Phi*X_hat(:,:,k) + Psi*u_wnoise + Gam*w_wnoise;
Z_til(:,:,k) = Z(:,:,k+1) - H*X_predict(:,:,k);
X_hat(:,:,k+1) = X_predict(:,:,k) + K(:,:,k+1)*Z_til(:,:,k);
Z_hat(:,:,k) = H*X_predict(:,:,k);
end
🎉3 参考文献
[1]张美英,何杰.时间序列预测模型研究综述[J].数学的实践与认识,2011,41(18):189-195.
