蓝桥杯备考
数论:判断素数,鸽笼定理,抽屉理论
注意事项:
组合剪枝:i < n - (k - path.size()) + 1
long类型的数后面要加L
long s = 2658417853L;
保留几位小数:
System.out.printf(“%.2f”, arg);
四舍五入问题:比如保留两位小数,就在数的后面再加0.005再保留小数,就不会有截断不入的情况。
BufferedReader和Scanner不能混用
整数转换成小数:1.0 * jigeSum
String转换成字符串数组:S.toCharArray()
long的范围是19位
Java异或:^
第二章 枚举、排列组合
手写子集
import java.util.*;
import java.io.*;
public class Main {
static int[] arr = {1,2,3,4,5,6,7};
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = arr.length;
for(int i = 1; i < (1 << n); i++) { //i从1~2^n,每一个i代表一个集合
//内循环按为与,结果非0则输出集合元素,j是1左移次数
for(int j = 0; j < n; j++) {
if((i & (1 << j)) != 0) {
System.out.print(arr[j]+" ");
}
}
System.out.println();
}
}
}
手写下一个排列:

排列组合
组合:用startIndex记录每次递归起始数,循环里i=startIndex
组合剪枝:i < n - (k - path.size()) + 1
不重复组合无限制选取数据:递归里的下一层startIndex=i
重复组合无限制选取数据:for循环不能重复,排序后 if(arr[i] == arr[i - 1]) continue;
排列直接i=0,但是要用数组记录上一层是否使用过
尺取法
应用场景:滑动窗口,[L, R],R随着L增大而增大
记忆化搜索
应用场景:多次查询
多次查询一定要储存
第三章 递推与递归
没什么东西
第四章 搜索
DFS 和 BFS
第五章 二分与并查集
二分查找
应用场景:最小值最大化,最大值最小化
必须有单调性!!
模板题:最终结果取right
三个地方特别容易记混:
1、求mid公式是否+1(这个记因为最小<最大,所以找最小不加,找最大+1)
2、while循环带不带等号(这个自己测试吧实在没想到好的记忆方法)
3、更新high和left哪个+1:这个好理解,哪个满足条件哪个=mid,不满足条件+1
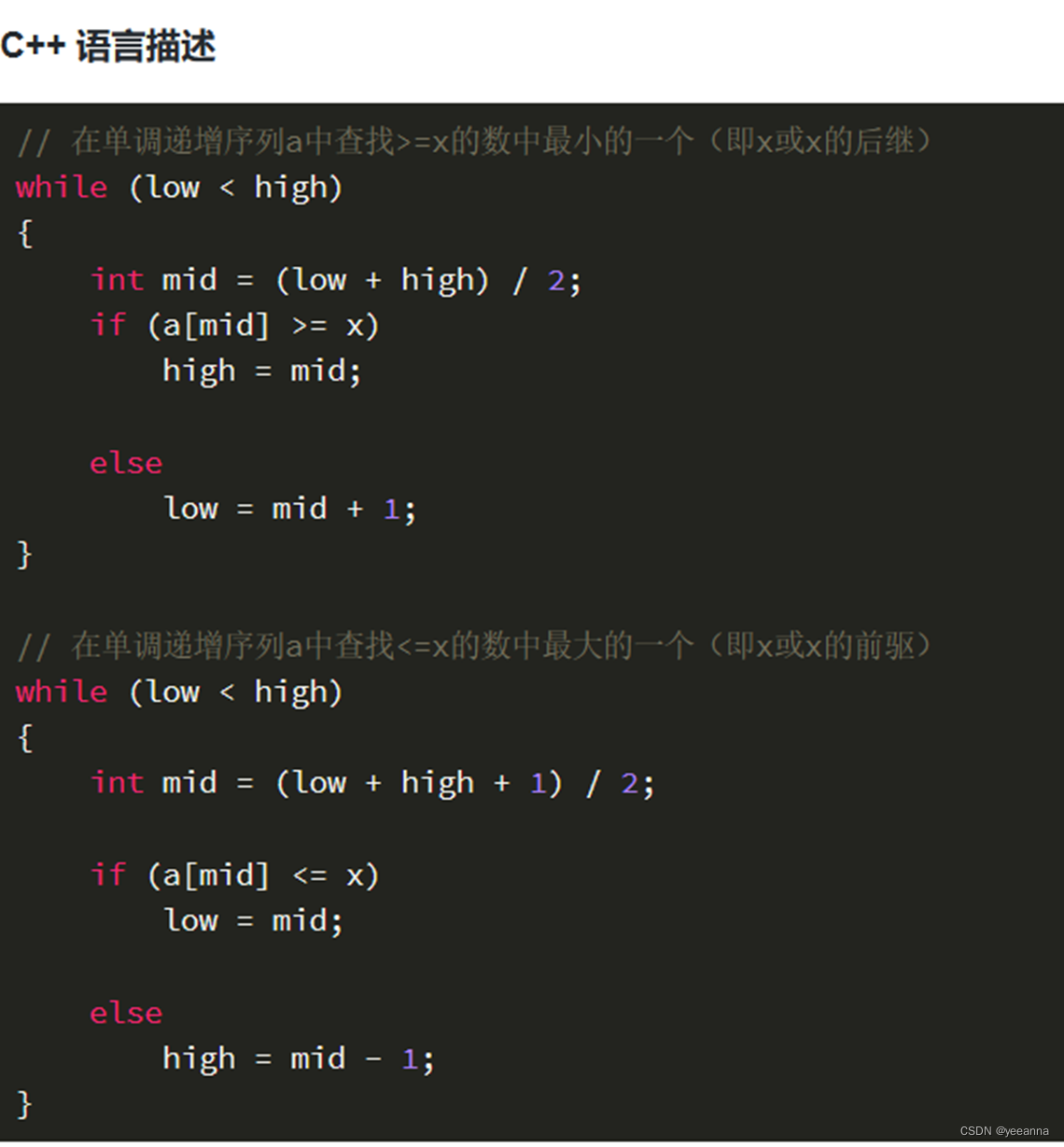
实数二分


注意循环结束条件是左右区间距离很小就行了。
并查集
1、存储

2、查询
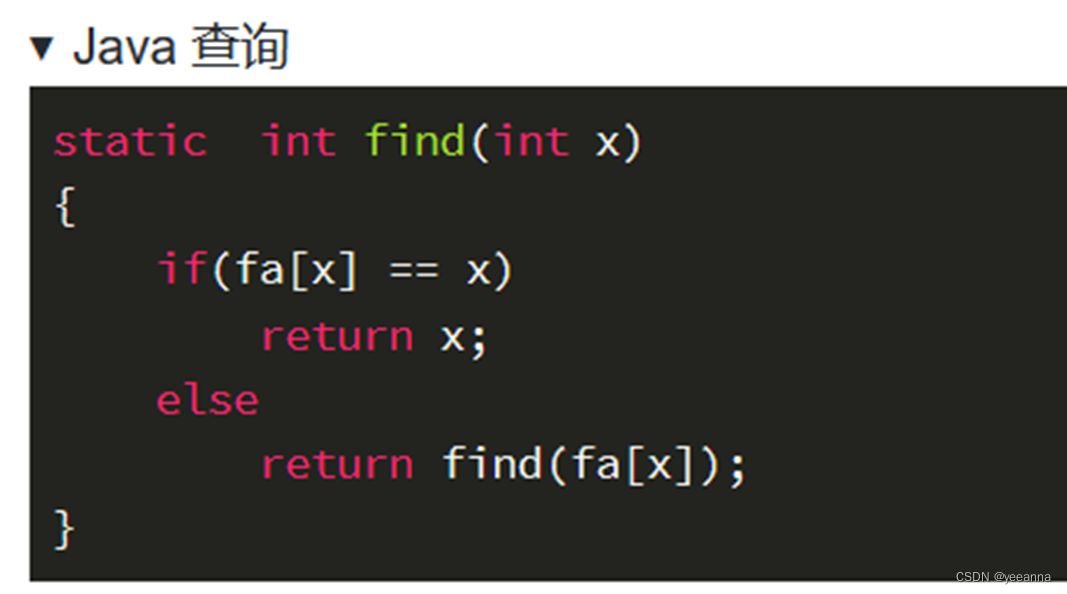
路径压缩:(记忆化递归)

3、集合合并
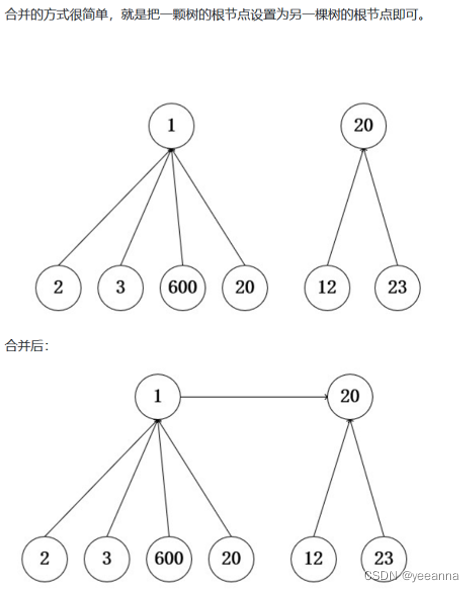
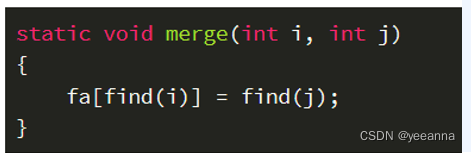
第六章 贪心
选择必须无后效性,当前选择不能影响后序选择对结果的影响
区间调度:按结束时间排序,选结束早的
区间覆盖:按左端点排序,选结束晚的
注意熟悉结构体排序:
Arrays.sort(goods, (Comparator<Goods>)(Goods x, Goods y) -> {
return -Double.compare(x.d, y.d);
});
第七章 动态规划
背包
dp[i][j]: 装第i个物品,装到重量为j的背包,最大价值是dp[i][j]
遍历顺序一般先物品后背包
0-1背包 滚动数组倒叙
多重背包滚动数组正序
多重背包 计数问题 组合是先物品后背包(横着填),排列是先背包后物品(竖着填)
快速幂

第八章 数论
快速幂
模运算的性质:(ab) mod k = (a mod k)(b mod k) mod k
求(b^p) mod k
先把b对k取模
把p分解成2的指数,p向右循环移位再与1表示乘不乘b
乘一次模一次
public static long mod(long a, long n, long k) {// a^n mod k
a %= k;
long ans = 1; //最终结果
while(n != 0) {
if((n & 1) != 0) {
ans = (ans * a) % k;
}
a = (a * a) % k;
n = n >> 1;
}
return ans;
}
Java大数:BigInteger
最大公约数gcd
辗转相除法

LCM最小公倍数

素数判断

素数筛

分解质因子

图论
Floyd算法:求两两相邻的点的最短路径。
判断负圈:dp[i][i] < 0
dp[i][j] = Math.max(dp[i][j], dp[i][k]+dp[k][j])
代码需要注意的问题:
- 用邻接矩阵存图,dp是邻接矩阵
- 邻接矩阵需要初始化成INF
- 图的起点是1,所以最好把1作为数组起点!!
- 别忘了输入可能有起点=终点的情况!此时路径为0
Dijkstra算法:求一个点到所有点的最短路径
不能处理负权值,不能判断负圈
SPFA:求一个点到所有点的最短路径
判断负圈:超过n轮,最短路径还有变化
邻接矩阵初始化等于INF的INF取多少合适?
dis[a,b] = dis[a,k] + dis[k,b]
INF = max/2
INF = -1也可以(最好用这个)
邻接矩阵不能存储重边。如果有重边,取最小值
迪杰斯特拉:不能处理负权值



Java:

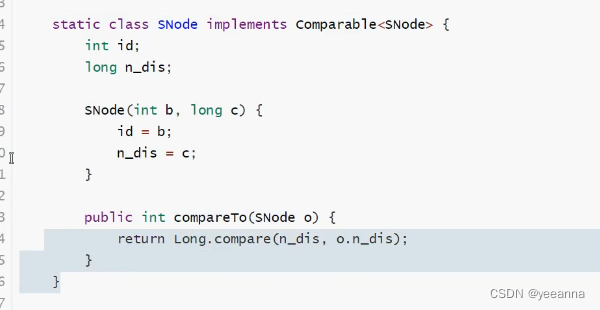


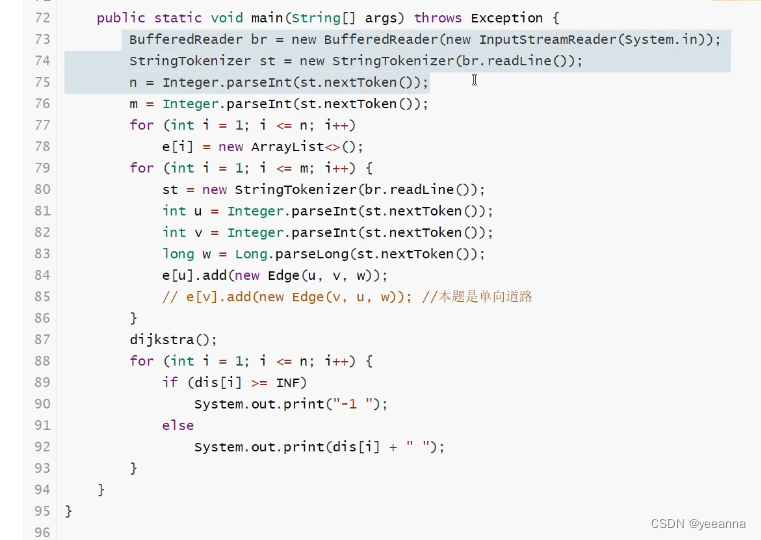
SPFA:
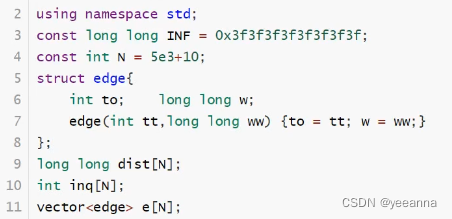


Java
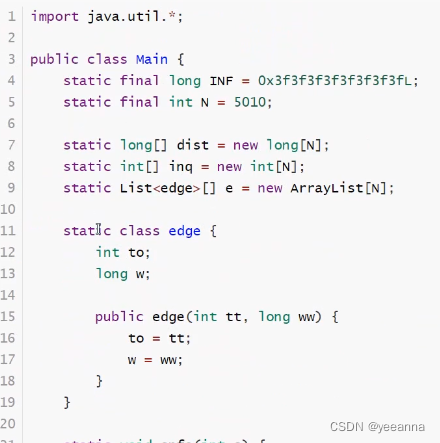


排序
import java.util.*;
import java.io.*;
public class 排序 {
public static void main(String[] args) {
Integer[] arr = {23,1,14,56,33,7};
Comparator cmp = new myCompare();
Arrays.sort(arr, cmp);
for(Integer i : arr) {
System.out.println(i);
}
}
}
class myCompare implements Comparator<Integer> {
public int compare(Integer o1, Integer o2) {
return -Integer.compare(o1, o2);
}
}
Map<Long, Integer> map = new TreeMap<>(new Comparator<Long>() {
@Override
public int compare(Long o1, Long o2) {
return (int)(o1 - o2);
}
});
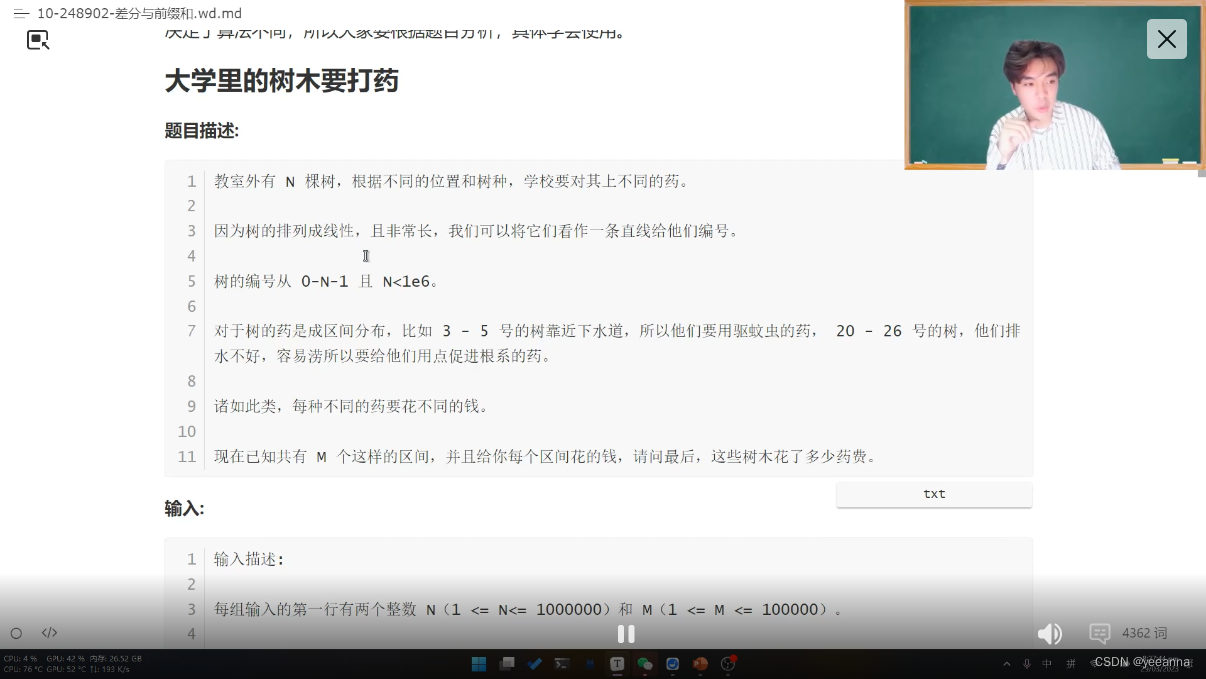
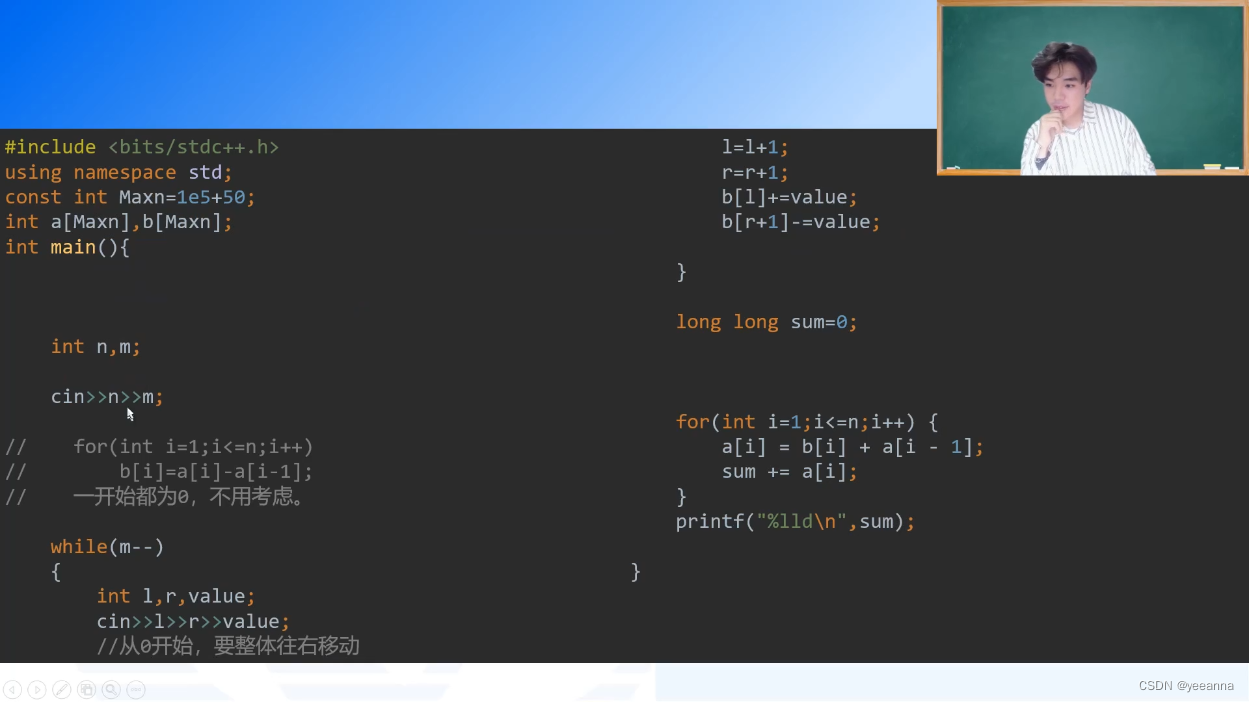
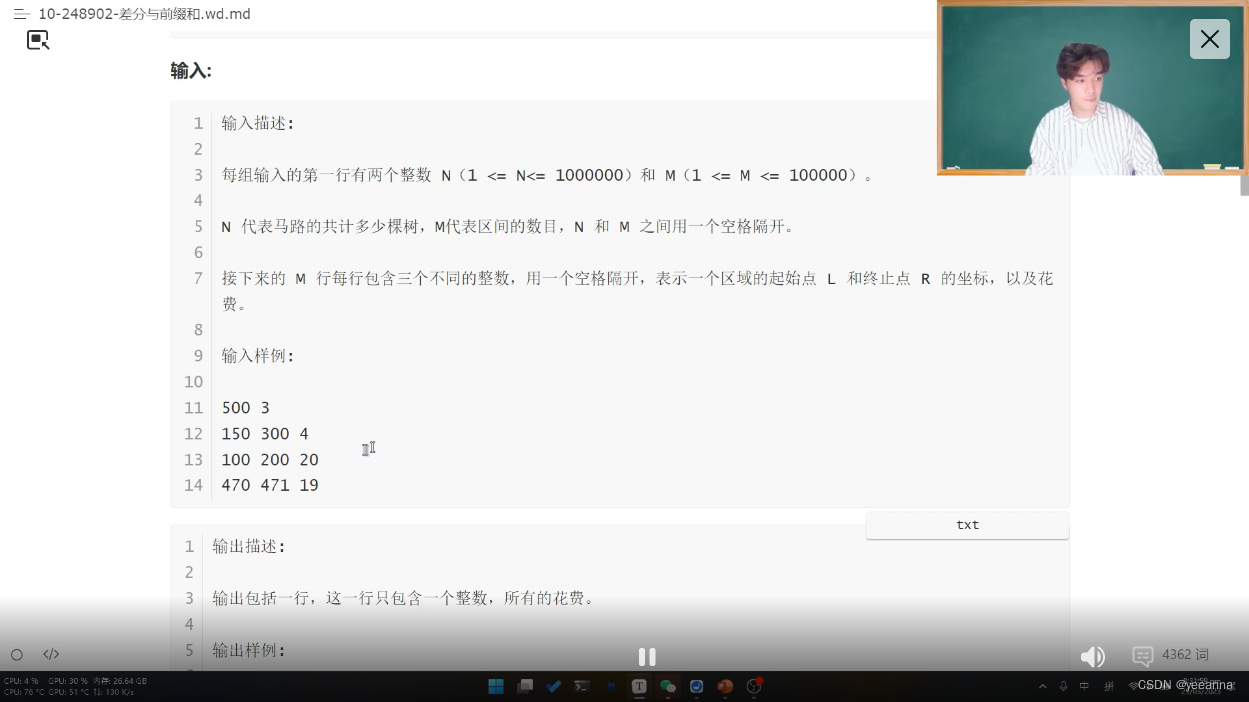
差分
求差分数组的时候要在原数组前补0,以便求查分数组第一个数
b[left] + value
b[right + 1] - value
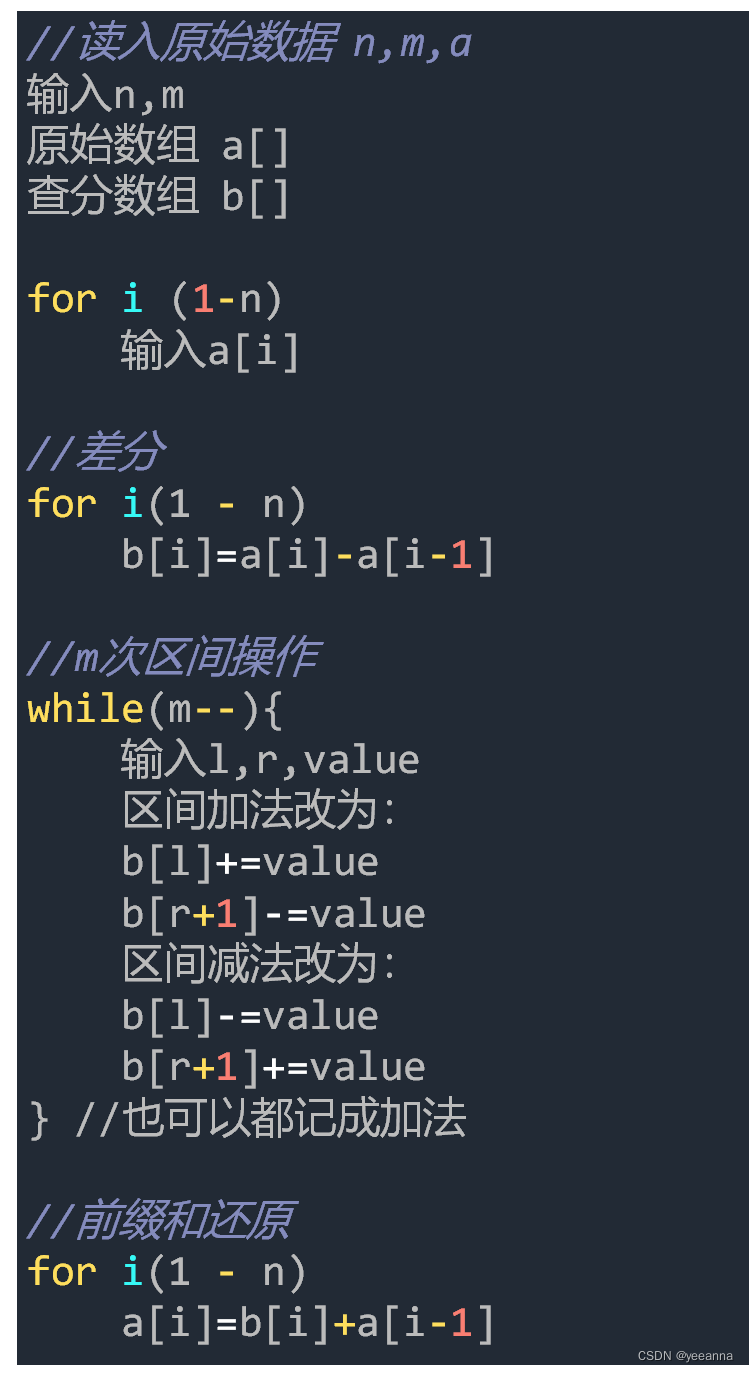

思维题:
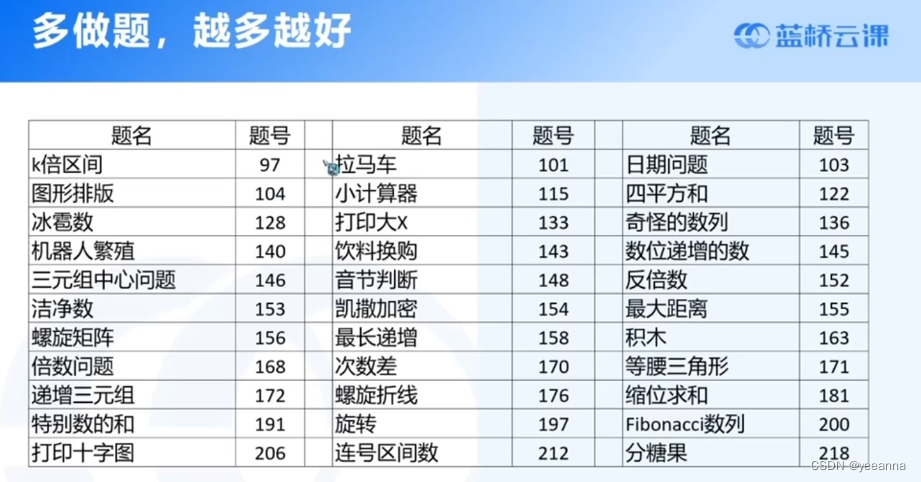

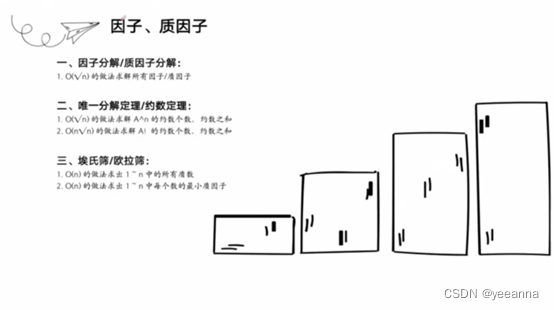
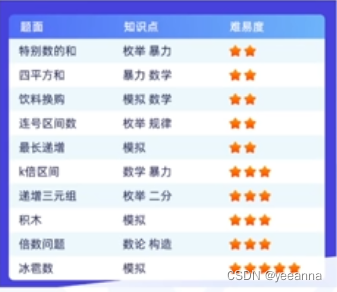
1s可以处理10^8个数据
Java语法
输入
Scanner input=new Scanner(System.in);
String str=input.next(); //String类型
int n=input.nextInt();//int类型
输出
System.out.printf(“%d %d %d %d\n”, a, b, c, d);
注意事项
输出的类型要和它规定的类型保持一致。比如要输出整数,就不能System.out.print(i+“ ”);
如何判断闰年
能被4整除却不能被100整除或能被400整除的年份






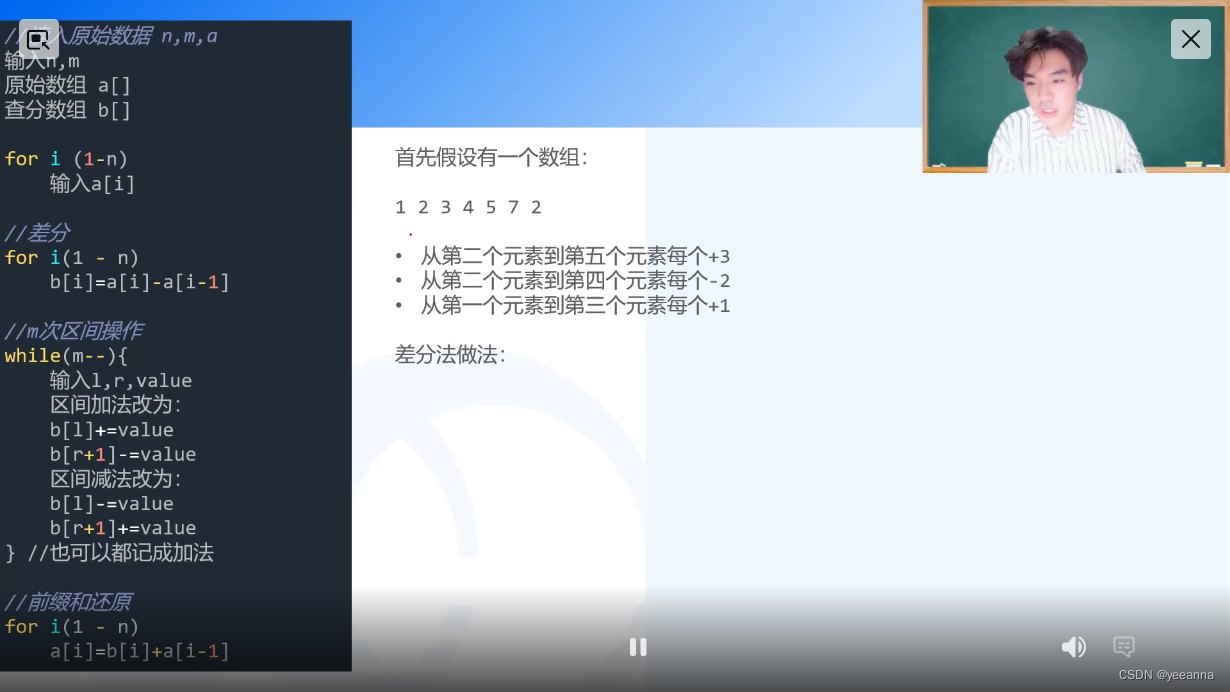
差分:区间左端点+value,区间右端点-value
前缀和和差分是互逆操作
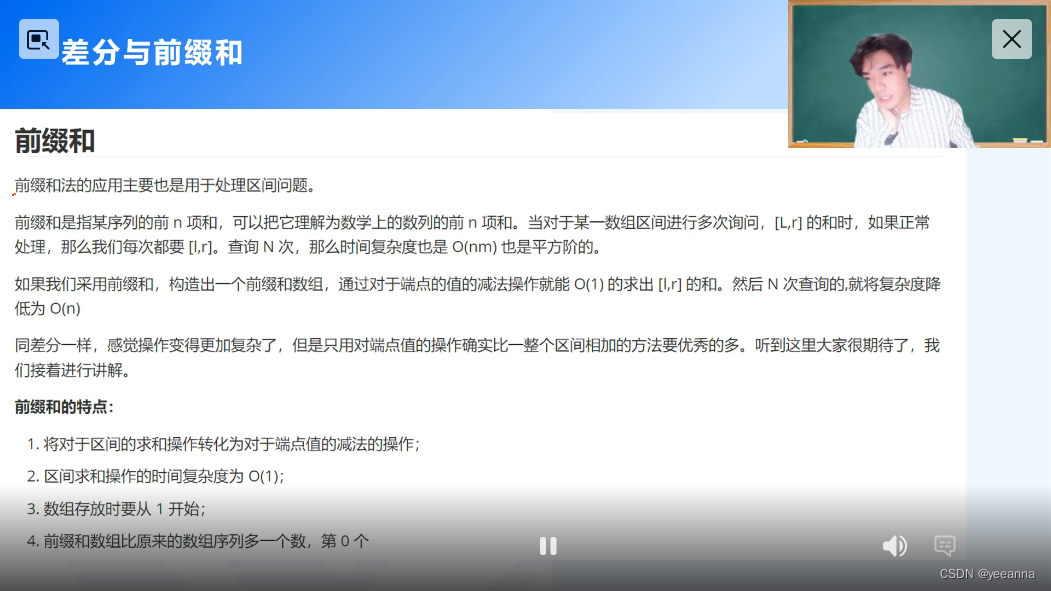

不能单独考前缀和和差分,仅仅是加速算法工具

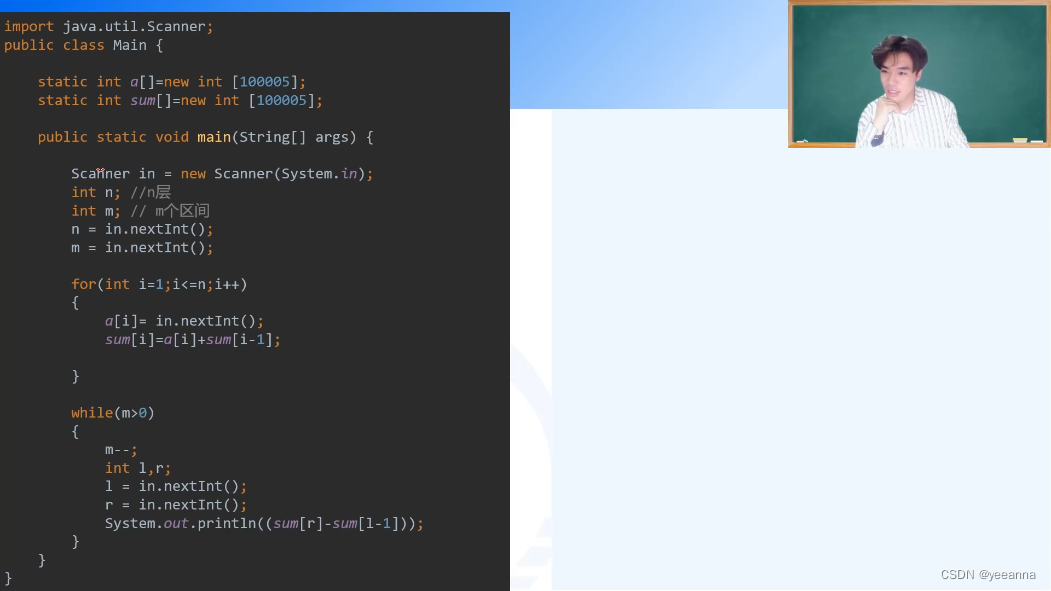
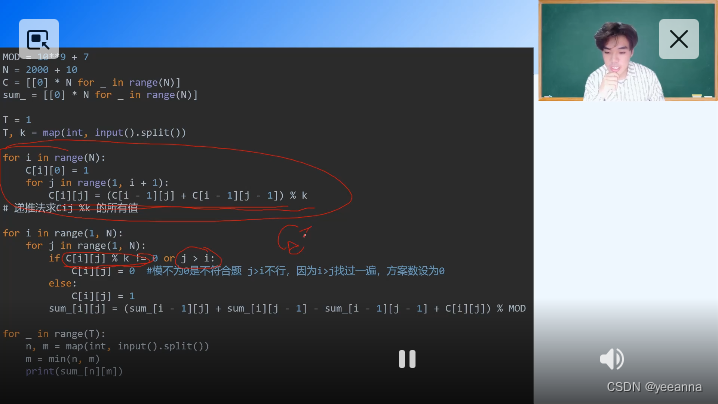
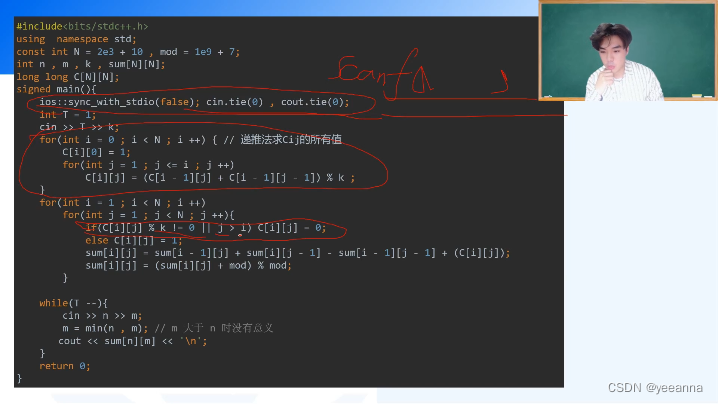
看看组合数问题

最好用静态数组,定义在main外面


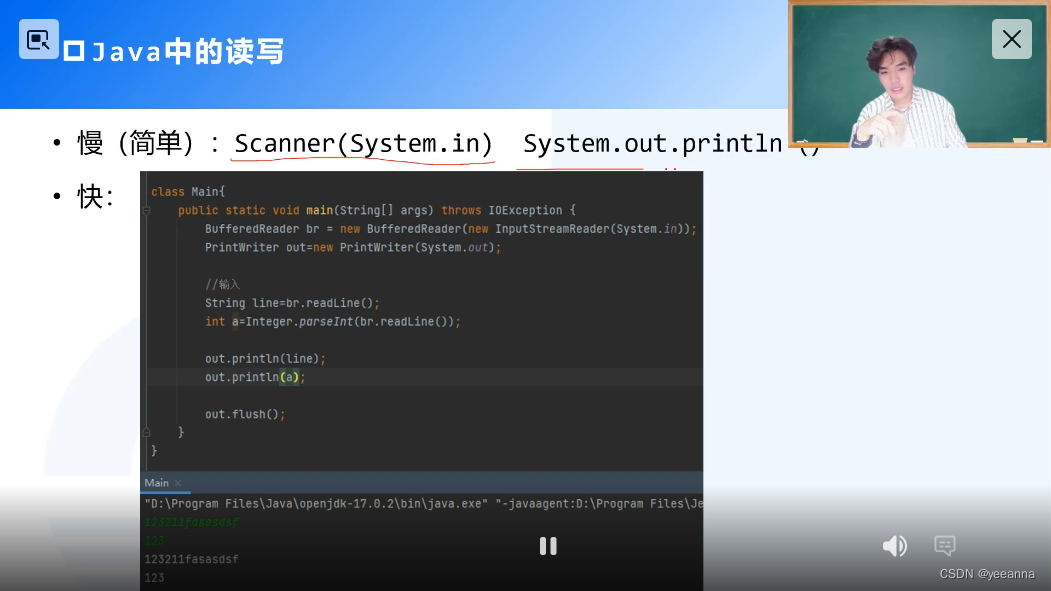

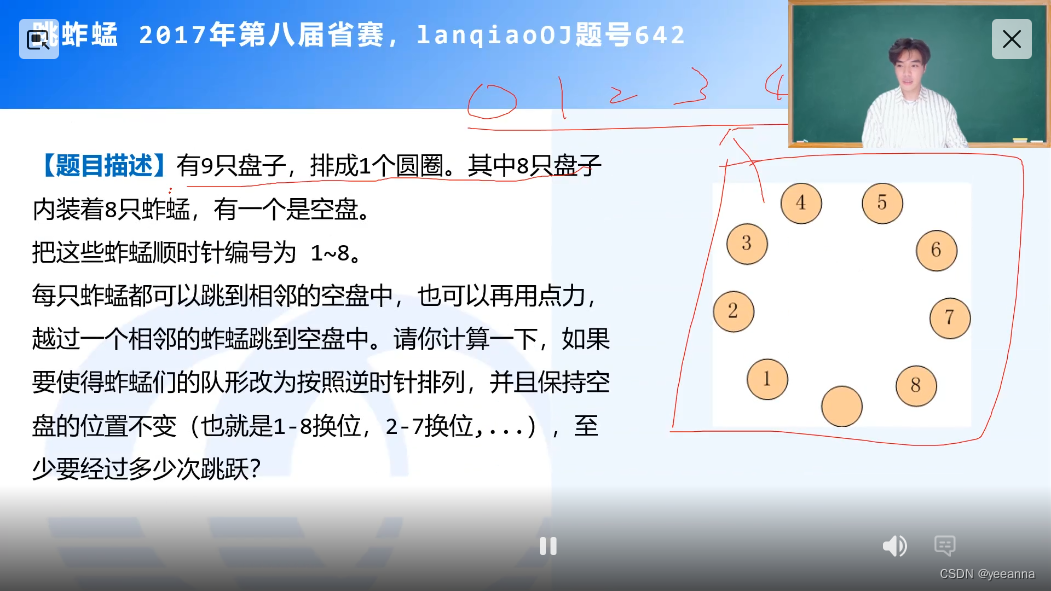

经常遍历用list,经常get用vector
数学公式:半径、面积


spfa 弗洛伊德
注意事项
