说明

闵老师的文章链接： 日撸 Java 三百行（总述）_minfanphd的博客-CSDN博客

自己也把手敲的代码放在了github上维护：https://github.com/fulisha-ok/sampledata

day14 栈

1.栈的特点

栈：后进先出,只能在栈顶操作。是先移动“指针”还是先移动数据，在出栈和进栈时要保持一致。当进栈操作时，先将数据存入，“指针”再做加一操作；当出栈时，先将数据取出，“指针”再做减一操作。

2.代码

package datastructure.stack;

public class CharStack {
    /**
     * The max depth.
     */
    public static final int MAX_DEPTH = 10;
    /**
     * The actual depth
     */
    int depth;
    /**
     * The data
     */
    char[] data;

    /**
     * Construct an empty char stack.
     */
    public CharStack(){
        depth = 0;
        data = new char[MAX_DEPTH];
    }

    /**
     * Overrides the method claimed in Object, the superclass of any class.
     * @return
     */
    @Override
    public String toString(){
        String resultString = "";
        for (int i = 0; i < depth; i++){
            resultString += data[i];
        }

        return resultString;
    }

    /**
     * Push an element
     * @param paraChar The given char.
     * @return Success or not.
     */
    public boolean push(char paraChar){
        if (depth == MAX_DEPTH){
            System.out.println("Stack full.");
            return  false;
        }

        data[depth++] = paraChar;

        return true;
    }

    public char pop(){
        if (depth == 0){
            System.out.println("Nothing to pop.");
            return '\0';
        }

        return data[--depth];
    }

    public static void main(String[] args) {
        CharStack tempStack = new CharStack();

        for (char ch = 'a'; ch < 'm'; ch++){
            tempStack.push(ch);
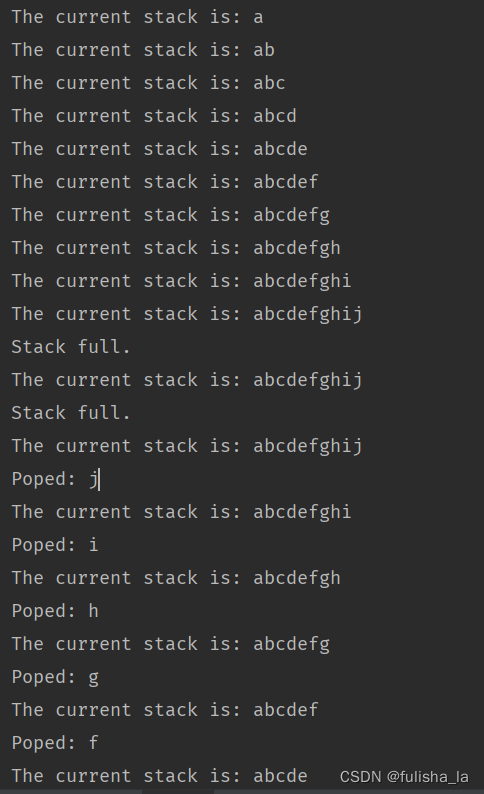
            System.out.println("The current stack is: " + tempStack);
        }

        char tempChar;
        for (int i = 0; i < 12; i++){
            tempChar = tempStack.pop();
            System.out.println("Poped: " + tempChar);
            System.out.println("The current stack is: " + tempStack);
        }
    }
}

运行结果

day15 栈的应用-括号匹配

1.思路

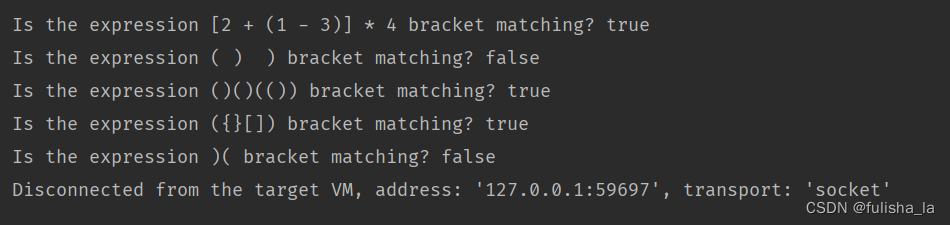
• 任务描述: 检查一个字符串的括号是否匹配. 所谓匹配, 是指每个左括号有相应的一个右括号与之对应, 且左括号不可以出现在右括号右边. 可以修改测试字符串, 检查不同情况下的运行.
• 思路：如(),[],{}括号左右对称，我们将括号分为左右，左括号入栈（遇到其他字符直接跳过不处理），遇到右括号就出栈一个左括号与之匹配，匹配成功即匹配，失败则不匹配。不要忘记在最后要判断一下栈中括号是否出栈完。在这里使用的是switch…case来进行判断分支，但是若换成if，else if，else来实现，则代码中会出现很多的分支，显然会显得代码很冗余，所以当分支较多时，使用switch相比if会好一些。

2.代码

    /**
     * Is the bracket matching?
     * @param paraString The given expression.
     * @return Match or not.
     */
    public static boolean bracketMatching(String paraString){
        //step1  Initialize the stack through pushing a '#' at the bottom.
        CharStack tempStack = new CharStack();
        tempStack.push('#');
        char tempChar, tempPopChar;

        //step2 Process the string. For a string, length() is a method instead of a member variable.
        for (int i = 0; i < paraString.length(); i++){
            tempChar = paraString.charAt(i);

            switch (tempChar){
                case '(':
                case '[':
                case '{':
                    tempStack.push(tempChar);
                    break;
                case ')':
                    tempPopChar = tempStack.pop();
                    if (tempPopChar != '('){
                        return false;
                    }
                    break;
                case ']':
                    tempPopChar = tempStack.pop();
                    if (tempPopChar != '['){
                        return false;
                    }
                    break;
                case '}':
                    tempPopChar = tempStack.pop();
                    if (tempPopChar != '{'){
                        return false;
                    }
                    break;
                default:
                    //do nothing
            }
        }
        tempPopChar = tempStack.pop();
        if (tempPopChar != '#'){
            return false;
        }
        return true;
    }

day16 递归

1.递归特点

• 理解：自己调用自己的方法，但是不能无限制的调用，在合适的时候又要一层层跳出自己方法最后跳出。在使用递归时，我觉得不能把问题考虑的太细，不然会陷入这个循环中把自己给绕晕，既然每个子问题规律一样，只需要知道他们规律，剩下交给计算机处理。在递归过程中，一定要保证有跳出递归的条件还有就是递归函数不一定效率就很高，如会受递归的深度、递归函数的实现方式等影响。当递归深度较大时，可能会导致堆栈溢出，从而影响程序的性能。

2.代码

• 递归实现1到n的和
  如果n小于0，则返回0作为结果。
  如果n大于0，则递归调用函数，并返回n加上递归调用函数的结果。
• 斐波那契数列
  F(0) = 0
  F(1) = 1
  F(n) = F(n-1) + F(n-2) (n >= 2)

package datastructure.stack;
public class Recursion {

    /**
     * Sum to N. No loop, however a stack is used.
     * @param paraN
     * @return
     */
    public static int sumToN(int paraN){
        if (paraN<0){
            return 0;
        }

        return sumToN(paraN-1) + paraN;
    }

    /**
     * Fibonacci sequence.
     * @param paraN The given value.
     * @return The sum.
     */
    public static int fibonacci(int paraN){
        if (paraN <= 0){
            return 0;
        }else if(paraN == 1){
            return 1;
        }

        return fibonacci(paraN-1) + fibonacci(paraN-2);
    }

    public static void main(String[] args) {
        int tempValue = 5;
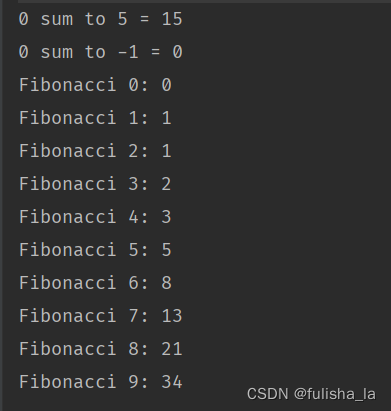
        System.out.println("0 sum to " + tempValue + " = " + sumToN(tempValue));
        tempValue = -1;
        System.out.println("0 sum to " + tempValue + " = " + sumToN(tempValue));

        for(int i = 0; i < 10; i ++) {
            System.out.println("Fibonacci " + i + ": " + fibonacci(i));
        }
    }
}