当前位置： 首页 > article >正文

动态规划之线性DP

article 2024/11/15 9:56:04

文章目录

  • 定义
  • 题单
    • Acwing题单
      • AcWing 898. 数字三角形（模板题）
      • AcWing 895. 最长上升子序列（模板题）
      • AcWing 896. 最长上升子序列 II（模板题，优化贪心）
      • AcWing 897. 最长公共子序列（模板题）
      • AcWing 902. 最短编辑距离（模板题）
      • AcWing 899. 编辑距离（模板题，等同于902题）
  • 参考资料

定义

线性DP是指我们的递推方程是存在一个明显线性的递推关系。可以是一维线性的、二维线性的、三维线性的、…

image-20230331202049829

  • 类似于这样子一行一行来求，背包问题就是二维的。

最长上升子序列模型属于线性DP。

从枚举的角度来考虑。

题单

Acwing题单

AcWing 898. 数字三角形（模板题）

题目链接：AcWing 898. 数字三角形

分析：从顶部开始出发（可以将其看成最终的一个出口）来进行递推，题目说从顶至底左下方或右下方来求得一条最大路径，我们也可以从底部来开始向上推导。

思路1：从上至下来推出所有的最大的路径，最后来去找到最后一行路径中的最大值。

状态方程：f(i, j)，移动到第i行第j个位置的最大值
初始化：默认都为0
转移方程：f(i, j) += max(f(i - 1, j - 1), f(i - 1, j))

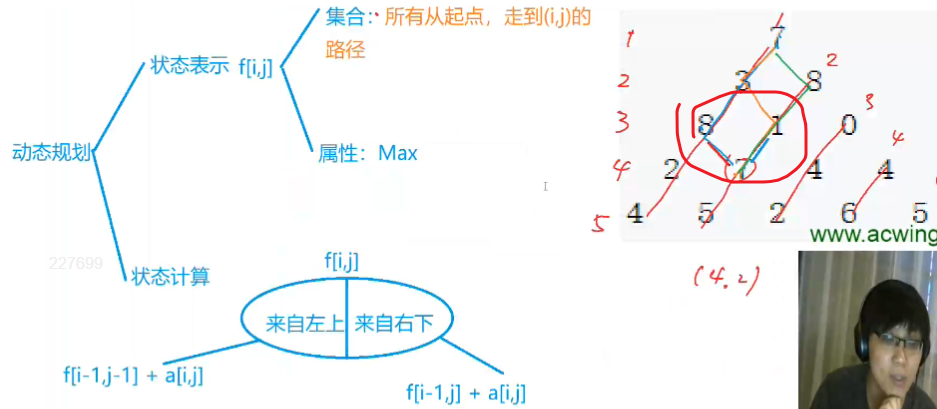
image-20230401111525514

从红圈中我们可以看到每一个点的最大路径值都是依据左上角与右上角来推算得到的，所以我们可以利用分治的思想来进行递推解决。

需要注意的一些点：①由于从上往下的推的话，可能会用到边界的无用值，注意题目中说明了数字三角形里面有负数，所以我们需要将边界的无用值去填充负无穷，这样才能够确保路径值相对正确。

image-20230401113753572

②由于每一层的状态都是由上一层的下相同第j个点以及其之前的状态值，所以我们在改动为滚动数组的时候需要从后往前。

思路2：从下至上进行不断递推，第一行第一个即为路径最大值。

状态方程：f(i, j)，移动到第i行第j个位置的最大值
初始化：默认都为0
转移方程：f(i, j) += max(f(i + 1, j), f(i + 1, j + 1)) + a[i][j]

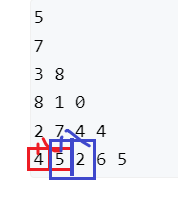
image-20230401113900009

而对于从下至上，无需使用到使用到边界值情况，所以可以直接填充为0也可以AC，并且这里滚动数组由于每次都是使用下一层对应当前点以及之后的点所以可以直接从前往后。

题解：

题解1：从上至下，一维滚动数组

复杂度分析：时间复杂度O(n2)；空间复杂度O(n)

import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 510;
    static int[][] a = new int[N][N];
    static int[] fn = new int[N];//更改为滚动数组
    static int n;
    
    public static void main(String[] args) throws Exception{
        n = Integer.parseInt(cin.readLine());
        
        //接收值
        for (int i = 1; i <= n; i ++) {
            String[] ss = cin.readLine().split(" ");
            for (int j = 1; j <= i; j ++) {
                a[i][j] = Integer.parseInt(ss[j - 1]);
            }
        }
        
        //初始化dp为负无穷
        for (int i = 0; i <= n; i ++) fn[i] = Integer.MIN_VALUE;
        fn[1] = a[1][1];//第一个数字进行初始化
        
        for (int i = 2; i <= n; i ++) { //从第二层开始
            for (int j = i; j >= 1; j --) { //可以看到转移方程使用到了上一层之前的状态，所以需要从后往前进行遍历
                //转移方程：fn(i, j) = max (fn(i - 1, j - 1), fn(i - 1, j)) + a[i][j]
                fn[j] = Math.max(fn[j - 1], fn[j]) + a[i][j];
            }
        }
        
        //找到最后一层最大路径值
        int res = fn[1];
        for (int i = 2; i <= n; i ++) {
            res = Math.max(res, fn[i]);
        }
        System.out.println(res);
    }
    
}

image-20230401113353359

题解2：从下至上，一维滚动数组

复杂度分析：时间复杂度O(n2)；空间复杂度O(n)

import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 510;
    static int[][] a = new int[N][N];
    static int[] fn = new int[N];//更改为滚动数组
    static int n;
    
    public static void main(String[] args) throws Exception{
        n = Integer.parseInt(cin.readLine());
        
        //接收值
        for (int i = 1; i <= n; i ++) {
            String[] ss = cin.readLine().split(" ");
            for (int j = 1; j <= i; j ++) {
                a[i][j] = Integer.parseInt(ss[j - 1]);
            }
        }
        
        for (int i = n; i >= 1; i --) { //从最后一层开始
            for (int j = 1; j <= i; j ++) { //可以看到转移方程使用到了上一层当前第j个以及之后的状态，可以直接从前往后遍历
                //转移方程：fn(i, j) = max (fn(i + 1, j), fn(i + 1, j + 1)) + a[i][j]
                fn[j] = Math.max(fn[j], fn[j + 1]) + a[i][j];
            }
        }
        //fn[1]即为最终的一个最大路径值
        System.out.println(fn[1]);
    }
    
}

image-20230401114334094

AcWing 895. 最长上升子序列（模板题）

题目链接：AcWing 895. 最长上升子序列

题目：给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。

分析：注意数值严格单调递增的子序列并不是说让你来去求得连续的，而是说让你求得这一块区域中保持递增的最大子序列长度。

状态方程：f(i)，表示以a[i]为结尾的严格单调上升子序列。

转移方程：f(i) = max(f(j) + 1, f(i))【j = 1, 2, 3, 4 … i - 1，且a[j] < a[i]】

image-20230401152501817

代码：

复杂度分析：时间复杂度O(n2)；空间复杂度O(n)

import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 1010;
    static int[] a = new int[N], fn = new int[N];
    static int n;
    
    public static void main(String[] args) throws Exception{
        n = Integer.parseInt(cin.readLine());
        String[] ss = cin.readLine().split(" ");
        for (int i = 1; i <= n; i ++) {
            a[i] = Integer.parseInt(ss[i - 1]);
        }
        //转移方程
        for (int i = 1; i <= n; i ++) {
            //找到每前i-1个最大值+1
            fn[i] = 1;
            //每次确定基于当前i最大的上升序列数量
            for (int j = 1; j < i; j ++) {
                if (a[i] > a[j]) {
                    fn[i] = Math.max(fn[i], fn[j] + 1);
                }
            }
        }
        //最后来找到1-n中最大的方案情况
        int res = 0;
        for (int i = 1; i <= n; i ++) {
            res = Math.max(res, fn[i]);
        }
        System.out.println(res);
    }
    
}

image-20230401152700073

AcWing 896. 最长上升子序列 II（模板题，优化贪心）

题目链接：AcWing 896. 最长上升子序列 II

分析：对比I中，整数的数量多了100倍，若是依旧按照上面的方案会超时，那么就需要进行优化。当前这个解法实际上不太像是DP，更像是贪心，但是其是由DP思想转变过来的，所以归在DP这类中。

建议初步看这篇博客学习理解：AcWing 896. 最长上升子序列 II

针对于上面这篇博客简洁描述：实际上这个栈【不用于记录最终的最长子序列】，而是【以stk[i]结尾的子串长度最长为i】或者说【长度为i的递增子串中，末尾元素最小的是stk[i]】。理解了这个问题以后就知道新进来的元素要不就在末尾增加，要不就替代从前往后第一个大于等于它元素的位置。

  • 每次替换元素都是，增加了序列长度增长的潜力！！！

详细思路理解版可看：AcWing 896. 最长上升子序列 II，中间包含有一个二分check。

//目标：在区间总找到第一个>=目标元素的位置
a[mid] > a[i]   r = mid  
a[mid] < a[i]   l = mid + 1
a[mid] = a[i]   r = mid

针对于=mid情况时，为什么r=mid呢？而不是r = mid - 1，可看如下情况：

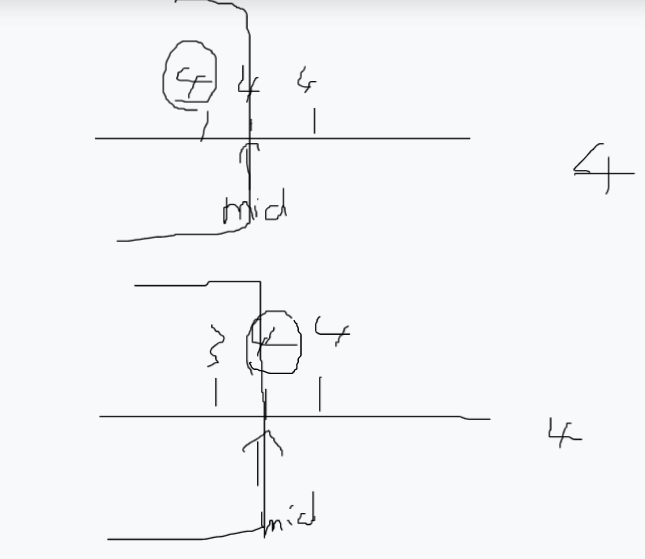
image-20230401163330718

题解：二分+贪心（单调队列）

复杂度分析：时间复杂度O(n.logn)；空间复杂度O(n)

import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 100010;
    static int[] a = new int[N], q = new int[N];
    static int n, cnt;
    
    //二分写法
    public static int find (int num) {
        int l = 1, r = cnt;
        while (l < r) {
            int mid = l + r >> 1;
            //若是目标元素值>=num，此时范围为[l, mid]
            if (q[mid] >= num) r = mid;
            else l = mid + 1;//若是<num，则需要直接到右半部分去寻找，范围为[mid + 1, r]
        }
        return r;
    }
    
    public static void main(String[] args) throws Exception{
        n = Integer.parseInt(cin.readLine());
        String[] ss = cin.readLine().split(" ");
        for (int i = 1; i <= n; i ++) a[i] = Integer.parseInt(ss[i - 1]);
        
        //进行单调队列，若是添加数>末尾数，直接添加到末尾；若是<=，则找到队列中>=该添加数的第一个数(从前往后)
        q[++ cnt] = a[1];
        for (int i = 2; i <= n; i ++) {
            if (a[i] > q[cnt]) {
                q[++ cnt] = a[i];
            }else {
                //替换从前往后第一个>=a[i]的位置
                q[find(a[i])] = a[i];
            }
        }
        System.out.println(cnt);
    }
    
}

image-20230401162305464

AcWing 897. 最长公共子序列（模板题）

题目链接：AcWing 897. 最长公共子序列

题目：给定两个长度分别为 N 和 M 的字符串 A和 B，求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。

分析：

定义方程：f(i, j)中i表示第1个序列的前i个字母中出现，j表示第二个序列中前j个字母中出现。

举例：注意子序列并非是连续，而是只要是公共拥有的公共子序列。

image-20230401170841756

针对于第一个前i个以及第二个前j个的子序列可以划分为四个子集。用0表示不选，1表示选。

  • f(i - 1, j - 1)：两个都不选，00
  • f(i - 1, j)：第i个不选，第j个选，01
  • f(i, j - 1)：第i个选，第j个不选，10
  • f(i - 1,j - 1) + 1：两个都选，11

其中第二个状态【第i个不选，第j个选是包含在f(i - 1, j)当中的】，第三个状态【第i个选，第j个不选是包含在f(i , j - 1)当中的】，实际上f(i - 1, j)、f(i, j - 1)都是将f(i - 1, j - 1)包含在内的。

转移方程：

  • a[i] != a[j]：max (a(i - 1, j)，a(i, j - 1))【实际上由于a(i - 1, j)和a(i, j - 1)是包含a(i - 1, j - 1)所以我们可以省略掉a(i - 1, j - 1)；原本是max (a(i - 1, j)，a(i, j - 1), a(i - 1, j - 1))】
  • a[i] == a[j]：f(i - 1, j - 1) + 1

注意点：在这里由于我们求得是max，所以可以在有交集的两个集合中a(i - 1, j)，a(i, j - 1)去选的一个最大值，若是求和就不行了！

  • 因为一个交集求得最大值，另一个交集也求得最大值，此时我们再求两个交集的最大值和直接求整个集合最大值得到的结果是一致的，若是其他的求和情况就不能够直接这样子在有交集的集合中求。

学习理解：AcWing 897. 最长公共子序列

题解：

复杂度分析：时间复杂度O(n*m)；空间复杂度O(n*m)

import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 1010;
    static int n, m;
    static char[] a = new char[N], b = new char[N];
    static int[][] fn = new int[N][N];
    
    public static void main (String[] args) throws Exception{
        String[] ss = cin.readLine().split(" ");
        n = Integer.parseInt(ss[0]);
        m = Integer.parseInt(ss[1]);
        //拷贝："abcd" => " abcd"（仅仅只为了之后a[i] == b[j]；也可以不拷贝直接接收，此时判断为a[i - 1] == b[j - 1]）
        char[] tempA = cin.readLine().toCharArray();
        System.arraycopy(tempA, 0, a, 1, n);
        char[] tempB = cin.readLine().toCharArray();
        System.arraycopy(tempB, 0, b, 1, m);
        for (int i = 1; i <= n; i ++) {
            for (int j = 1; j <= m; j ++) {
                //不等于的情况
                fn[i][j] = Math.max(fn[i - 1][j], fn[i][j - 1]);
                if (a[i] == b[j]) //由于i与j从1开始，所以这里比较的时候-1
                    fn[i][j] = Math.max(fn[i][j], fn[i - 1][j - 1] + 1);
            }
        }
        System.out.println(fn[n][m]);
    }
    
}

image-20230401182022259

AcWing 902. 最短编辑距离（模板题）

AcWing 902. 最短编辑距离

分析：

上图：

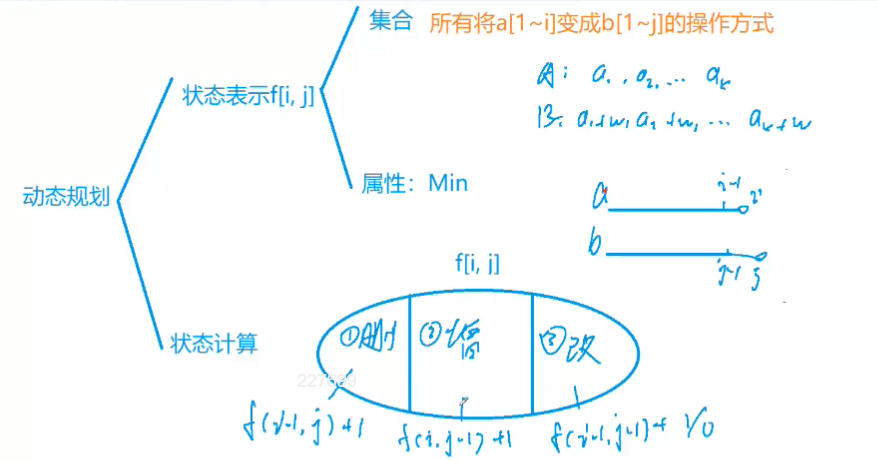
image-20230401205541408

接着我们来针对不同的情况进行讨论：

①插入：f(i, j - 1) + 1

image-20230401211527268

②删除：f(i - 1, j) + 1

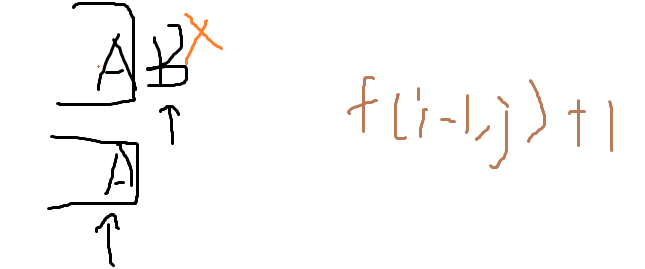
image-20230401211929611

③替换：

情况1两者不等：f(i - 1, j - 1) + 1

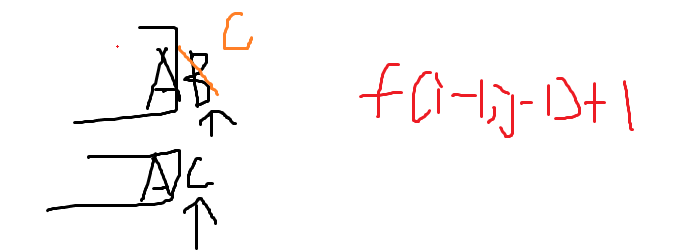
image-20230401212109256

情况2两者相等：f(i - 1, j - 1)

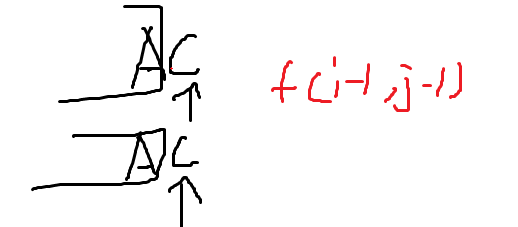
image-20230401212222929

方程定义：f(i, j)将A中1-i个字符变为B中的1-j个字符。

初始化：

  • i = 0，j = 1,2,3…5：f(0, j) = j
  • i = 1, 2, 3…n，j = 0：f(i, 0) = i

转移方程：

  • 删除与插入情况：min(f(i - 1, j) + 1, f(i, j - 1) + 1)
  • a[i] == b[j]：min(f(i, j), f(i - 1, j - 1))
  • a[i] != b[j]（需要进行替换操作一次）: min(f(i, j), f(i - 1, j - 1) + 1)

学习理解：AcWing 902. 最短编辑距离、最短编辑距离（线性DP）

题解：

复杂度分析：时间复杂度O(n*m)；空间复杂度O(n*m)

import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 1010;
    static char[] a, b;
    static int[][] fn = new int[N][N];
    static int n, m;
    
    public static void main(String[] args) throws Exception{
        n = Integer.parseInt(cin.readLine().trim());
        a = cin.readLine().toCharArray();
        m = Integer.parseInt(cin.readLine().trim());
        b = cin.readLine().toCharArray();
        
        //初始化 0->1,2,3,4,5  (i->j) 插入操作
        for (int j = 0; j <= m; j ++) {
            fn[0][j] = j;
        }
        //       1,2,3,4,5 -> 0 (i->j) 删除操作
        for (int i = 0; i <= n; i ++) {
            fn[i][0] = i;
        }

        //最短编辑距离操作
        for (int i = 1; i <= n; i ++) {
            for (int j = 1; j <= m; j ++) {
                //删除与插入操作
                fn[i][j] = Math.min(fn[i - 1][j], fn[i][j - 1]) + 1;
                if (a[i - 1] == b[j - 1]) {
                    fn[i][j] = Math.min(fn[i - 1][j - 1], fn[i][j]);
                }else {
                    fn[i][j] = Math.min(fn[i - 1][j - 1] + 1, fn[i][j]);//替换动作
                }
            }
        }
        System.out.println(fn[n][m]);
    }
    
}

image-20230401213614424

AcWing 899. 编辑距离（模板题，等同于902题）

题目链接：AcWing 899. 编辑距离

分析：

本题实际上就是在902题模板题上套了一个多次询问，其实并没有什么其他的优化点，只需要每次将一个字符串与n个进行计算转换的次数来检测是否是<=给定的最大范围长度并计算数量即可。

时间复杂度为：1000*1000*10*10 = 1亿，刚好在差不多一秒内。

对应最短编辑距离题解可见：AcWing 902. 动态规划-线性DP 最短编辑距离（模板题）

题解：

复杂度分析：时间复杂度O(n.m.k2)；空间复杂度O(m*k)，n表示对比的单词串个数，m表示询问的次数，k表示的单词串的长度。

  • 由于单词的长度很小，每次去计算转换的时间复杂度为O(10*10)，即为O(k2)。
import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
    static final int N = 15, M = 1010;//N表示单词的长度，M表示单词的个数
    static char[][] s = new char[M][N];//存储所有的单词
    static int[][] fn = new int[N][N];
    static int n, m;
    
    public static int transfer(char[] a, char[] b) {
        int aL = a.length, bL = b.length;
        for (int i = 1; i <= aL; i ++) {
            for (int j = 1; j <= bL; j ++) {
                //插入、删除操作
                fn[i][j] = Math.min(fn[i][j - 1], fn[i - 1][j]) + 1;
                //编辑替换操作：若是i与j位置不同则需要进行替换操作
                fn[i][j] = Math.min(fn[i][j], fn[i - 1][j - 1] + (a[i - 1] == b[j - 1] ? 0 : 1));
            }
        }
        return fn[aL][bL];
    }
    
    public static void main(String[] args) throws Exception{
        String[] ss = cin.readLine().split(" ");
        n = Integer.parseInt(ss[0]);
        m = Integer.parseInt(ss[1]);
        for (int i = 1; i <= n; i ++) {
            s[i] = cin.readLine().toCharArray();
        }
        
        //初始化状态数组
        for (int j = 0; j < N; j ++) fn[0][j] = j;//添加
        for (int i = 0; i < N; i ++) fn[i][0] = i;//删除
        
        while (m -- != 0) {
            ss = cin.readLine().split(" ");
            String originStr = ss[0];
            int limit = Integer.parseInt(ss[1]);
            int res = 0;
            for (int i = 1; i <= n; i ++) {
                //获取最小的转换步数
                int step = transfer(originStr.toCharArray(), s[i]);
                if (step <= limit) res++;
            }
            out.println(res);
        }
        out.flush();
    }
    
}

image-20230402111730266

参考资料

[1]. 【动态规划】线性DP

[2]. AcWing 898. 数字三角形：y总视频讲解，很详细

[3]. 最长上升子序列 II 相关：AcWing 896. 最长上升子序列 II 这篇是该题的入门模板很推荐一看、AcWing 896. 最长上升子序列 II 这一篇相对来说比y总的题解代码更清晰明了

[4]. 最长公共子序列：AcWing 897. 最长公共子序列 y总视频讲解很详细很核心，


http://www.kler.cn/a/7991.html

相关文章：

  • 学习日志010--python异常处理机制与简单文件操作
  • Prometheus面试内容整理-Exporters
  • 深入探索：Scrapy深度爬取策略与实践
  • 机器学习【激活函数】
  • 手动实现promise的all，race，finally方法
  • WEB攻防-通用漏洞SQL注入sqlmapOracleMongodbDB2等
  • 基于凸集上投影（POCS）的聚类算法
  • Pycharm用ssh连接GCP以后，可以项目都放在本地，只是调用GCP的计算资源吗？
  • Vue+springboot+java学生成绩动态追踪系统课程资源课件下载设计与实现
  • 【Python】【进阶篇】三、Python爬虫的构建User-Agnet代理池
  • itext使用缺陷？
  • Linux下的shell编程（必须给予执行权限）
  • ChatGPT帮我和老板吵架，半分钟做了个思维导图...
  • jackson、fastjson、kryo、protobuf等序列化效率对比【全】
  • ospf综合实验
  • 【Spring Boot】自定义 Banner
  • WebSocket与HTTP联系及Socket的区别
  • VisualStudio如何进行OneNote插件开发？
  • 全文检索工具 Lucene 入门
  • 响应式布局是什么?如何实现响应式布局
  • 逻辑删除和唯一约束冲突的解决方案
  • springcloud：xxl-job的任务触发机制及调度过期策略
  • IT知识百科：什么是BGP？
  • ubuntu20.04 下载 linux源码和编译简单测试模块
  • Python 变量教程打包和解包参数
  • NHibernate教程_编程入门自学教程_菜鸟教程-免费教程分享