实验6 TensorFlow基础

1. 实验目的

掌握TensorFlow低阶API，能够运用TensorFlow处理数据以及对数据进行运算。

2.实验内容

①实现张量维度变换，部分采样等；
②实现张量加减乘除、幂指对数运算；
③利用TensorFlow对数据集进行处理。

3.实验过程

题目一：
加载波士顿房价数据集，并按照以下要求选择属性、计算并绘图。(20分)
⑴ 以二维数组的形式显示属性NOX、RM和LSTAT，其中每一行为一个样本，每一列为一个属性或房价。(4分)
⑵ 选择属性RM和房价，绘制散点图。其中每个样本的属性值为$x_i$，每个样本的房价为$y_i$, $i$为样本的索引值。(2分)
⑶ 使用TensorFlow分别计算$w$和$b$，并输出结果。(10分)

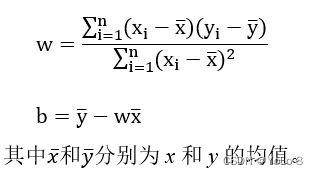
⑶ 以w为斜率，b为截距，做出一条直线，和第⑵问的散点图绘制在同一张图上。(3分)
⑷ 观察这条直线和散点之间的位置关系，你有什么发现或者猜测。(1分)

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
boston_housing = tf.keras.datasets.boston_housing

(train_x,train_y),(text_x,text_y) = boston_housing.load_data(test_split=0)

#设置rc参数
plt.rcParams["font.family"] = "SimHei"#设置默认字体为中文黑体
plt.rcParams['axes.unicode_minus'] = False #坐标轴上负号的显示可能会出错

titles = [
    "CRIM", "ZN", "INDUS", "CHAS", "NOX", "RM", "AGE", "DIS", "RAD", "TAX",
    "PTRATIO", "B-1000", "LSTAT", "MEDV"
]

nox = [[train_x[:,4]],[train_y]]
rm = [[train_x[:,5]],[train_y]]
latat = [[train_x[:,12]],[train_y]]

plt.figure(figsize=(4,4))

plt.scatter(train_x[:,5],train_y)
plt.xlabel("RM")
plt.ylabel("Price($1000's)")
plt.title(str(6)+ "." + "RM - Price")

x = tf.constant(train_x[:,5],tf.float32)
y = tf.constant(train_y,tf.float32)

average_x = tf.reduce_mean(x)
average_y = tf.reduce_mean(y)

sum1 = tf.reduce_sum(tf.multiply(tf.subtract(x,average_x),tf.subtract(y,average_y)))
sum2 = tf.reduce_sum(tf.square(tf.subtract(x,average_x)))

w = sum1 / sum2
b= average_y - w * average_x

#画拟合直线
x = np.linspace(4,9,50)
y = w * x  + b
plt.plot(x,y,color = "r")


print("W=%f",w)
print("b=%f",b)

plt.show()

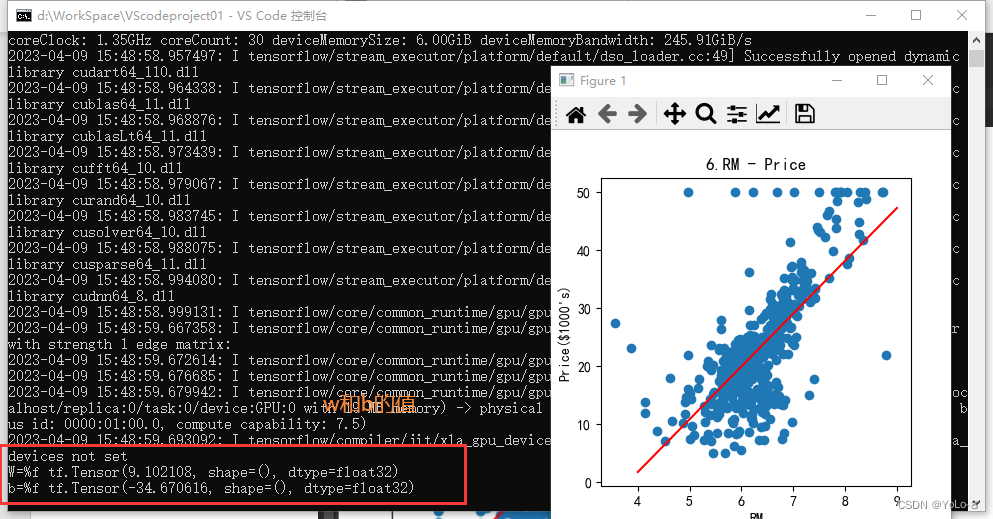
答：近似拟合为一条直线

题目二：
使用TensorFlow张量运算计算w和b，并输出结果。(20分)
已知：
x=[ 64.3, 99.6, 145.45, 63.75, 135.46, 92.85, 86.97, 144.76, 59.3, 116.03]
y=[ 62.55, 82.42, 132.62, 73.31, 131.05, 86.57, 85.49, 127.44, 55.25, 104.84]
计算:

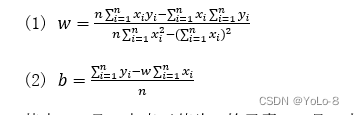
其中，$x_i$是x中索引值为i的元素；$y_i$是y中索引值为i的元素；n是张量中元素的个数；
(3)分别输出w和b的结果。

import tensorflow as tf

x = tf.constant([ 64.3, 99.6, 145.45, 63.75, 135.46, 92.85, 86.97, 144.76, 59.3, 116.03],tf.float32)
y = tf.constant([ 62.55, 82.42, 132.62, 73.31, 131.05, 86.57, 85.49, 127.44, 55.25, 104.84],tf.float32)

average_x = tf.reduce_mean(x)
sum1 = 10 * tf.reduce_sum(tf.multiply(x,y)) - tf.reduce_sum(x) * tf.reduce_sum(y)
sum2 = 10 * tf.reduce_sum(tf.square(x)) - tf.square(tf.reduce_sum(x))

w = sum1 / sum2
b = (tf.reduce_sum(y) - w * tf.reduce_sum(x) ) / 10

print("w = %f",w)
print("b = %f",b)

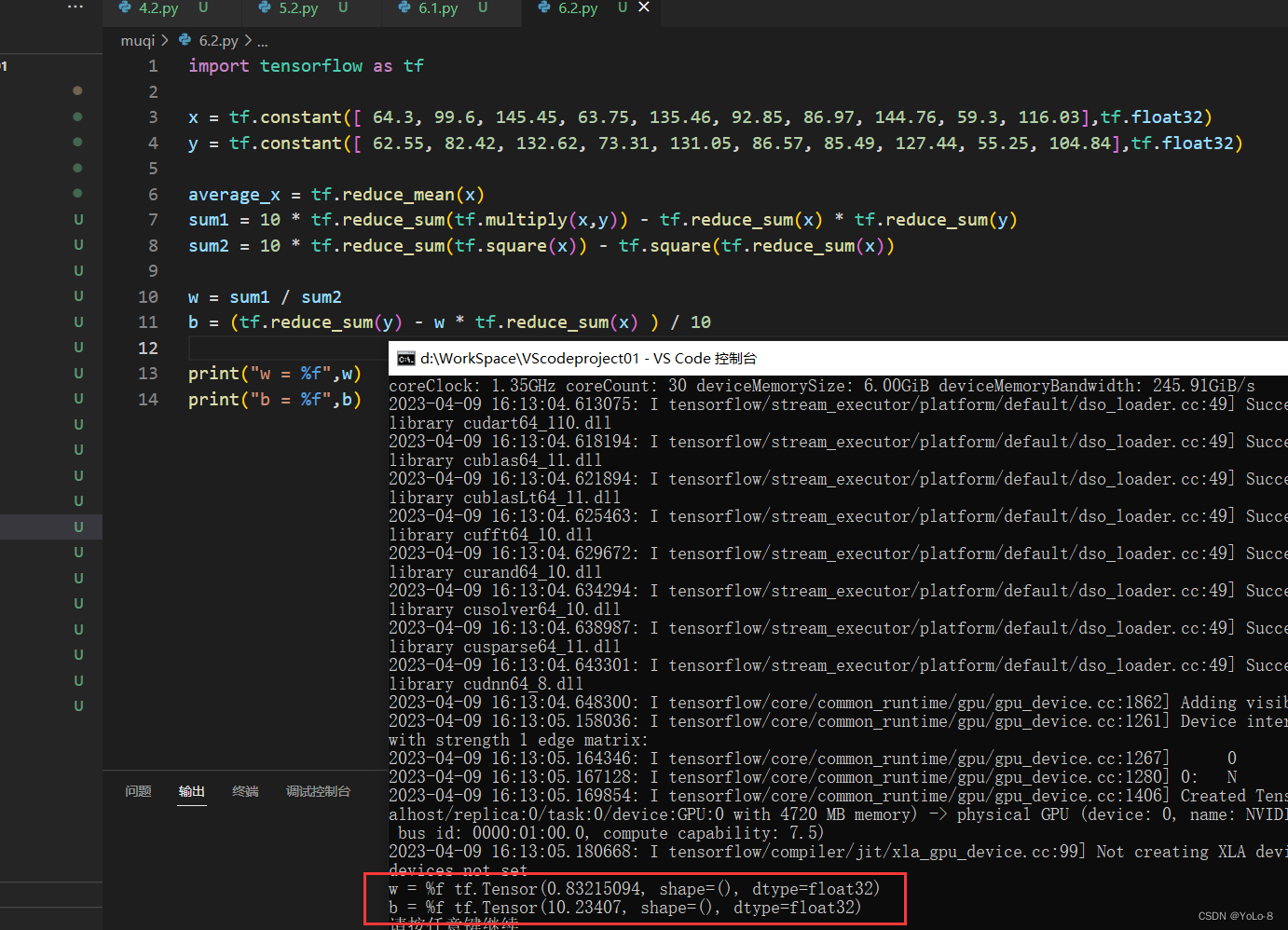
题目三：

已知：x1=[137.97, 104.50, 100.00, 124.32, 79.20, 99.00, 124.00,114.00, 106.69, 138.05, 53.75, 46.91, 68.00, 63.02, 81.26, 86.21]
x2=[3, 2, 2, 3, 1, 2, 3, 2, 2, 3, 1, 1, 1, 1, 2, 2]
y =[145.00, 110.00, 93.00, 116.00, 65.32, 104.00, 118.00,91.00, 62.00, 133.00, 51.00, 45.00, 78.50, 69.65, 75.69, 95.30]
按要求计算：(20分)
(1) 创建一个16×3的二维数组X，其中第一列全为1，第二列和第三列中分别为数组x1和x2中的数据，并输出。
(2) 将数组y转换为16×1的二维数组Y，并输出。
(3) 根据前两问得出的X和Y，利用如下公式，求W。

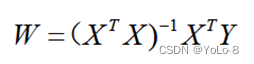
import tensorflow as tf

x1 = tf.constant([137.97, 104.50, 100.00, 124.32, 79.20, 99.00, 124.00,114.00, 106.69, 138.05, 53.75, 46.91, 68.00, 63.02, 81.26, 86.21],tf.float32)
x2 = tf.constant([3, 2, 2, 3, 1, 2, 3, 2, 2, 3, 1, 1, 1, 1, 2, 2],tf.float32)
y = tf.constant([145.00, 110.00, 93.00, 116.00, 65.32, 104.00, 118.00,91.00, 62.00, 133.00, 51.00, 45.00, 78.50, 69.65, 75.69, 95.30],tf.float32)


x0 = tf.ones(16,tf.float32)

X = tf.stack((x0,x1,x2),axis=1)

Y = tf.reshape(y,[16,1])

Xt = tf.transpose(X)

W = tf.linalg.inv(Xt @ X) @ Xt @ Y 

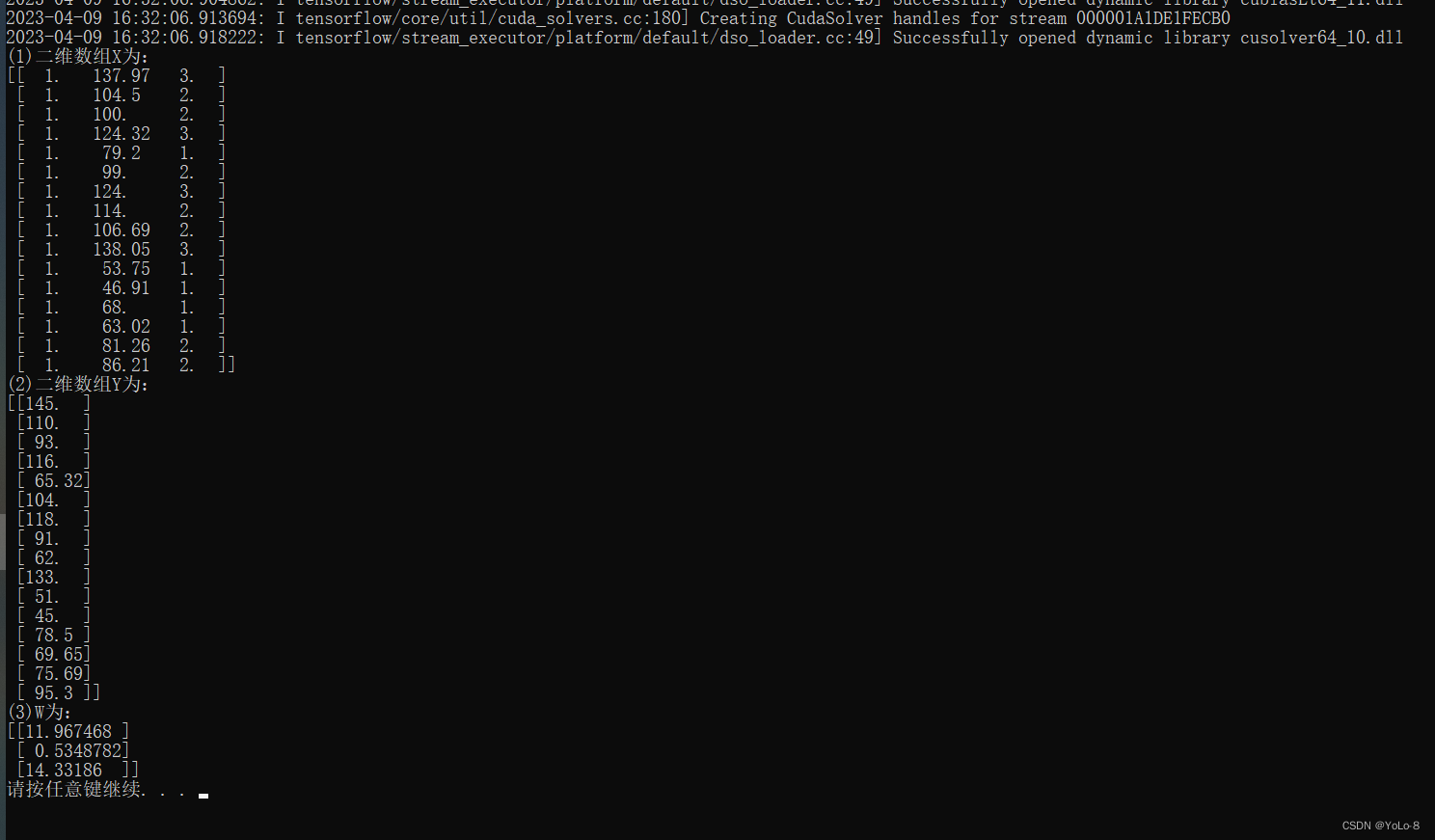
print("(1)二维数组X为：")
print(X.numpy())
print("(2)二维数组Y为：")
print(Y.numpy())
print("(3)W为：")
print(W.numpy())

4. 实验小结&讨论题

① 实验过程中遇到了哪些问题，你是如何解决的？
没有问题。

② 在实现数组运算时，采用NumPy和TensorFlow各有什么特点？你认为编程时如何选择或使用它们更合理？需要注意哪些问题？
Numpy是用来处理数组的科学计算库，其在深度学习兴起之前就已经存在，其不能很好的支持GPU计算，也不能支持自动求导。而tf正是为了弥补这些缺点而产生的。
在tf中我们经常会见到一些类型。Scalar代表一个标量（一维向量代表的是一个1*1的矩阵，其运算规则是遵循线性代数中的矩阵运算规则。而标量只是一个常数，它参与的是数乘运算。），其维度为0。Vector代表向量其维度为1，
Matrix代表一个矩阵。严格意义上的定义，当rank>2时，才能把矩阵叫做tensor，但是在TF中我们通常把维度为1的数据也可以叫做tensor。在此处从数学意义上说，不够严谨，但是在工程表达中没有差别。

③ 在题目基本要求的基础上，你对每个题目做了那些扩展和提升？或者你觉得在编程实现过程中，还有哪些地方可以进行优化？(可以从如何提高代码的简洁度来谈谈这个问题)
没有扩展和提升，按照题目要求写的。一堆重复的变量可以删除。