当前位置：首页 > article >正文

板块模型构建、k点选定及Miller指数对表面分类

article 2024/9/20 10:42:10

1表面的重要性

表面对于催化、界面科学、电子制造，半导体制造等很多领域都是非常重要的。理解表面的几何构型和电子结构十分有意义。在一些科研项目中，表面科学实验和DFT计算成功的结合在一起。DFT计算常常和超高真空表面科学的实验技术相结合，例如：扫描隧道显微镜（ $Scanning Tunneling Microscopy,STM$ )、程序升温脱附（ $Temperature Programmed Desorption$ ）、X射线光电子能谱（ $X-Ray Photoelection Spectroscopy$ ）,从而可以确定金属、金属氧化物、纳米颗粒、碳化物和硫化物的表面结构。例如，1959年通过对 $Si\left ( 111 \right )$ 表面进行电子衍射实验，表明该表面具有复杂对称性，并且形成表面的原子排列与体相 $Si$ 晶体结构完全不同。由于 $Si$ 在微电子技术的重要性，详细了解其表面结构是十分重要的。知道1992年才完成一个很大的超晶胞的DFT计算，从而对 $Si\left ( 111 \right )-\left ( 7\times 7 \right )$ 表面重构进行了有效性测试，并且该测试的认可度很高。这个计算不仅明确给出了该表面每个原子的位置，并且可以用于模拟该表面的STM成像，有助于解释实验所得图像。

下面将介绍如何用DFT计算考察固体表面。

2周期性边界条件和板块模型

当研究的对象是一个表面时，理想的模型应该是两个方向上无限大，在沿表面法线上有限大的一条长材料。为了在建模上实现这一点，可以在两个方向上应用周期性边界条件优势，在法线方向上不可以。虽然已经有相关计算软件能够实现这一点，但在研究表面的时候，更加普遍使用的计算程序

是在三个坐标方向上都应用了周期性边界条件。基本概念如下图所示，在超晶胞的竖直方向上。只有一部分区域含有原子。在超晶胞下部，这些原子在x和y方向上充满了整个超晶胞，但是在这些原子的上方，也就是超晶胞的顶部区域是没有原子的，因此这种模型称之为板块（ $slab$ ）模型。

当该超晶胞在所有三个方向上都重复时，就定义了一系列堆垛在一起的，并由空白区域所分隔开的固体材料板块。如下图所示。在z方向上分隔开周期性板块图像的空白区域称之为真空区（ $Vacuum Space$ ）。当使用这种模型块时一定需要足够大的真空区，以便材料的电荷密度在真空区逐渐消失为零，从而使板块的顶面与相邻板块的底面之间不存在作用。

下图所示就是在真空区内所观察使用这种方法所定义的原子视图，可以看到:超晶胞实质上定义了两个表面，一个是上表面，一个是下表面。

假设对 $FCC$ 金属（例如 $Cu$ ）的表面进行计算，应当如何建立上述的板块模型？使用超晶胞的晶格矢量分别和笛卡尔坐标系的 $x,y,z$ 轴一致，其中 $z$ 轴和超晶胞表面法线方向一致。对于fcc金属，其晶格常数与常规晶胞中立方体边长相等。超晶胞的矢量应该是：

$a_{1}=a(1,0,0)$ $a_{2}=a\left ( 0,1,0 \right )$ $a_{3}=a\left ( 0,0,5 \right )$

式中： $a$ 为晶格常数。

图4.1中原子的分数坐标是：

$\left ( 0.0,0.0,0.0 \right )$ $\left ( 0.5,0.5,0.0 \right )$

$\left ( 0.0,0.5,0.1 \right )$ $\left ( 0.5,0.0,0.1 \right )$

$\left ( 0.0,0.0,0.2 \right )$ $\left ( 0.5,0.5,0.2 \right )$

$\left ( 0.0,0.5,0.3 \right )$ $\left ( 0.5,0.0,0.3 \right )$

$\left ( 0.0,0.0,0.4 \right )$ $\left ( 0.5,0.5,0.4 \right )$

如上所述，定义了含有5层独立原子的板块，且在z方向上，两层原子间距为 $\frac{a}{2}$ ,真空区的宽度为 $3a$ 。对于该超晶胞，板块的每层原子均含有两个独立原子。在定义 $a_{3}$ 时，数值5有一点随意。但可以精确的是，该矢量必须做够大，从而保证该超晶胞具有足够的真空区；但真空区越大，则所需的计算量越大。在实际计算过程中，需要对若干个具有不同真空区宽度的模型，检验真空区的电荷密度，从而判断需要多少真空区才是对这个板块而言足够大的。理想情况是真空区边缘的电荷密度接近于0。如果读者想要做该测试，需要注意的是：在改变 $a_{3}$ 长度的同时，原子分数坐标的 $z$ 值也需要相应的调整，以保证材料中相邻两层原子之间是正确的物理间距。

（分数坐标与笛卡尔坐标

分数坐标是把点阵矢量看成是单位矢量下确定原子位置; 笛卡尔坐标是绝对坐标，是直角坐标系与斜角坐标系的统称，考虑点阵常数的大小。

Basically, the fractional coordinates show the fraction of each unit cell vector that contributes to the position of that atom。根本上来说，分数坐标给出了每个原子在元胞的相对位置

晶格参数：

A (Ax Ay Az) 2.46 0.00 0.00

B (Bx By Bz) -1.23 2.13 0.00

C (Cx Cy Cz) 0.00 0.00 10.00

一个点的分数坐标（a, b, c）（0.667 0.333 0）

x = Axa+Bxb+Cxc = 2.46*0.667-1.23*0.333+0*0=1.23

y = Aya+Byb+Cyc = 0*0.667+2.13*0.333+0*0=0.71

z = Aza+Bzb+Czc = 0*0.667+0*0.333+10*0=0

这个点的笛卡尔坐标（x, y, z） (1.23 0.71 0)

所以，笛卡尔坐标并不是原子在我们作为参考的直角坐标系中的绝对位置，而是在元胞基矢构成坐标系中，原子的绝对位置，而分数坐标，就是原子在元胞基矢构成坐标系中原子的相对位置。对于一个斜角坐标系，显然原子的相对位置比较好判断，所以，我们一般在POSCAR中用到的是其分数坐标，如果需要用到笛卡尔坐标，就用上面的公式转换。）

上述讨论中的板块模型包括有 $FCC$ 金属的5层原子。当然，一个真实表面时一块材料的最边缘部分，且除非在很特殊的情况下，一班材料都至少几微米厚，与上述5层表面模型完全不同。这就引出了一个问题：多少层原子才是具有现实意义的？通常而言，原子层数越多越好，但所用的原子层数越多，那么计算时间一定会延长。关于怎么判断原子层数已经达到足够收敛了，这一点取决于所研究材料的物质本性和所需计算的参数。如同真空区宽度一样，这个问题也可以通过如下方法找到答案：计算并观察某些特性（如表面能和吸附能）随着原子层数逇增加时如何变化的。在选定模型总的原子层数时，通常是在计算成本和物理精度之间进行折中。

3选定表面计算的 $K$ 点

对于板块计算，可以采用 $Monkhorst-Pack$ 方法选定 $k$ 点。为了进一步直观的了解这一点，可以计算一下与上述超晶胞相关的倒易晶格矢量。可得 $\left | b_{1} \right |=\left | b_{2} \right |=\frac{2\pi }{a}$ , $\left | b_{3} \right |=\frac{2\pi }{5a}$ 。因为超晶胞在实空间中晶格矢量越长，对应着在倒易空间越短。这表明在倒易空间中求解积分的近似解时，在 $b_{3}$ 方向上并不需要那么多的k点。对于该超晶胞，使用一个 $M_{1}\times M_{1}\times M_{2}$ 的 $k$ 点网格。其中，对于该几何构型而言， $M_{1}> M_{2}$ 是较为合适的。

超晶胞z方向上较大的尺寸包含了真空区，这一事实引入了另一个有关 $k$ 点的选择经验。如果真空区足够大，则在距离板块边缘很短的位置上，电荷密度就消失为0。这意味着：在 $b_{3}$ 方向上只使用一个 $k$ 点就能得到精确的结果。因此，对于板块计算常常使用 $M\times N\times 1$ 的 $k$ 点网格。其中，所选定的 $M$ 和 $N$ 能够在表面模型的晶面内，对其 $k$ 空间进行足够精确的取样。

4采用 $Miller$ 指数对表面分类

对于图4.3所示表面，可以想象成将体相晶体劈裂（ $Cleave$ ）后所形成的。真实的晶体劈裂，可以沿着不同晶面对晶体进行劈裂，形成不同晶体排列的表面。这意味着需要采用一种标注方法，用于定义所讨论的表面。

图4.4给出了 $Cu$ 表面的晶面与体相晶体结构的对应关系。该晶面的朝向可以用与与该晶面相垂直的法相矢量来描述。从下图可以看出，这个矢量的一个有效选择就是 $\left [ 0,0,1 \right ]$ ，也可以选择 $\left [ 0,0,2 \right ]$ 等相平行的矢量。

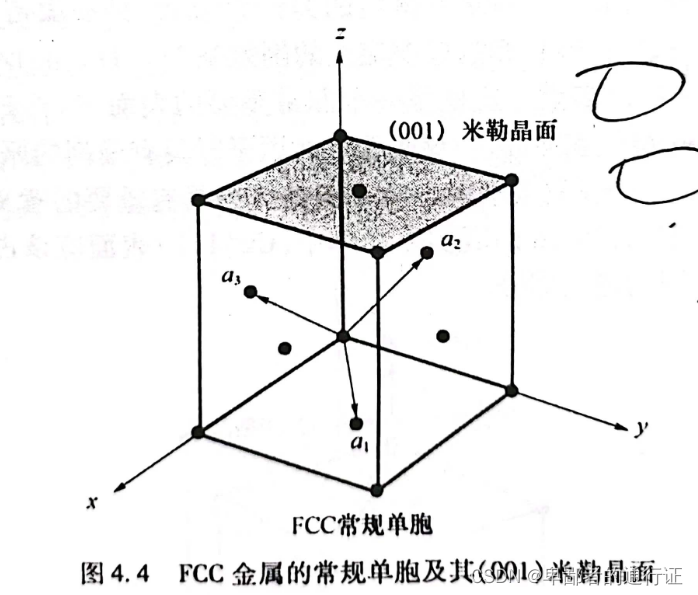
为了确定应该使用这些矢量中的哪一个，通常需要先确定该晶面与材料原胞 $\left ( Primitive Cell \right )$ 或者常规单胞 $\left ( Convetional Cell \right )$ 三轴的截交点。将这些截交点的倒数同乘以某个因子，从而将每个倒数都化成整数，并使每个倒数都尽可能小，最终所得的数值就称为该表面的 $Miller$ 指数。如上图所示，该晶面与常规单晶胞的 $z$ 轴相交于1（以晶格常数为单位），但是和 $x,y$ 轴并不相交，则这些截交点的倒数是（0,0,1），该表面可以表示成 $\left ( 001 \right )$ 。

如果定义该表面垂直方向的矢量需要加个负号，则其 $Miller$ 指数的相应分量上也要加个横杠。但对于这种晶体结构来说，由于对称性，不严格区分。

图4.5显示材料的另一种表面，该表面为 $\left ( 1,1,1 \right )$ 。这也是一个非常重要的表面，对于 $FCC$ 材料的所有 $Miller$ 指数表面而言，该表面的原子层具有较高的原子密度。也正是如此，这个表面在平衡态的真实晶体中具有重要的意义。上述讨论表明：在 $Cu$ 的真实多晶体中， $Cu$ $\left ( 111 \right )$ 表面应该占据了该晶体整个表面的绝大部分。

图4.6显示了 $Cu\left ( 110 \right )$ 表面，与z轴不相交。

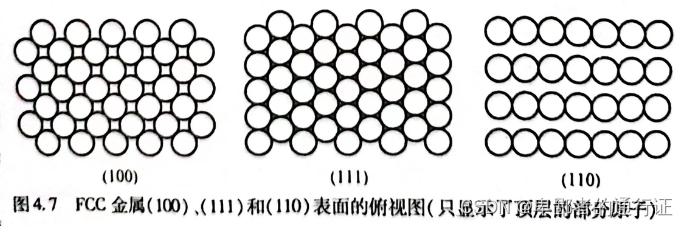
图4.7显示了 $FCC\left ( 001 \right ),\left ( 111 \right ),\left ( 110 \right )$ 表面的俯视图。这些试图给出了每个表面的不同对称性。这三种 $FCC$ 表面全是原子尺度的平直表面，即：任意种表面上的每个原子都具有相同的配位关系，且在表面法向上的坐标也相同。这些表面综合在一起称之为 $FCC$ 材料的低指数表面。其他晶体结构也具有自身的低指数表面，但与 $FCC$ 结构不同的是：其他结构的低指数表面往往具有不同的 $Miller$ 指数。例如，对于 $BCC$ 材料，其原子密度最高的表面是 $\left ( 110 \right )$ 表面。

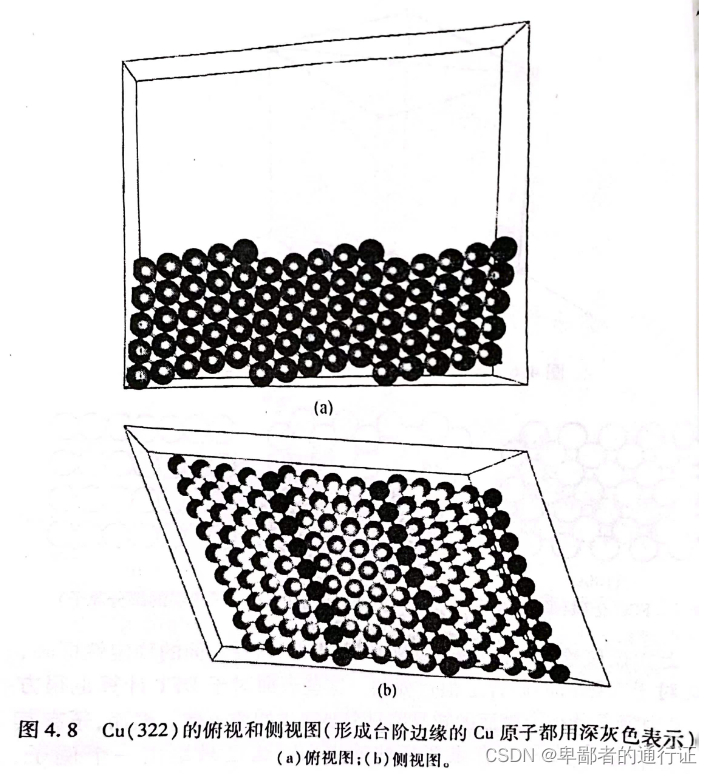
上文仅仅给出了低指数表面的一些示例这些表面的稳定性高，对于实际研究很重要。这些表面的 $DFT$ 计算也很方便，因为定义低指数表面的超晶胞只需要适当的原子数。图4.8是 $Cu\left ( 322 \right )$ 表面的俯视图和侧视图。该表面许多局部区域看起来很像 $\left ( 111 \right )$ 表面，并且这些区域均由一个原子高度的台阶所分隔开来。相比于表面上的其他原子，这些位于台阶边缘处的原子具有较低的配位数，这往往导致具有更高的反应活性。在催化合成氨时，台阶边缘的反应活性原子就扮演着至关重要的作用。尽管 $Cu\left ( 322 \right )$ 要比低指数表面更为复杂，但是该表面的晶面任然具有周期性，因此任然可以使用超晶胞来描述该表面。