当前位置：首页 > article >正文

算法题：图的表示形式与遍历框架

article 2024/11/15 6:20:41

图的基本概念

在数据结构和算法上，图的数据表示一般使用邻接表和邻接矩阵的形式。

比如：

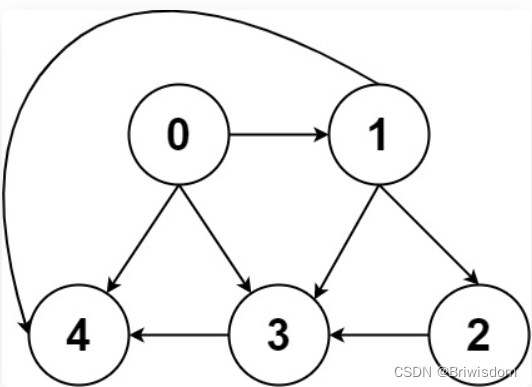
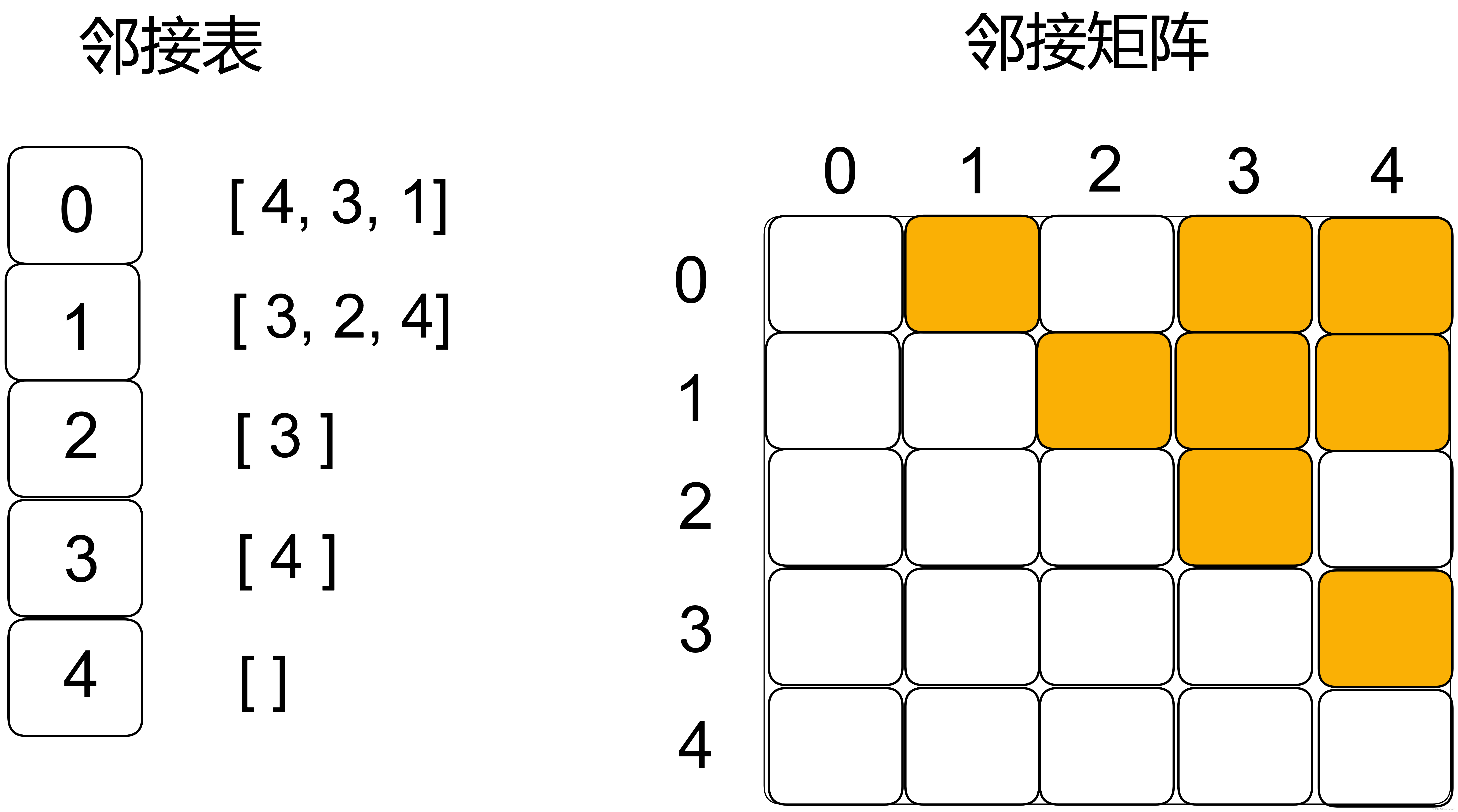
邻接表和邻接矩阵存储如下。邻接表是用vector[vector[i]] 存储每个节点指向的节点，邻接矩阵是用一个二维矩阵matrix[i][j]表示，如果第数据的i维和j维元素为true（黄色），表示这里存在节点i到j的连接。

和邻接矩阵相比，邻接表更省存储空间，但是无法快速判断两个节点是否相连(比如判断i到j, 需要找到i个节点对应的vector,然后判断j是否存在。

再明确一个图论中特有的度（degree）的概念，在无向图中，「度」就是每个节点相连的边的条数。由于有向图的边有方向，所以有向图中每个节点「度」被细分为入度（indegree）和出度（outdegree），比如上面的有向图中，节点3的出度为3（有3条边指向它），出度为1（有1条边指向别的节点）。

加权有向图值的是，有向图中节点之间的连接加了权重值，比如在邻接矩阵中，matrix[i][j]不再是布尔值，而是一个int值，0表示无连接，其他值表示连接权重。

图的遍历

各种数据结构被发明出来，无非就是为了遍历和访问，遍历是所有数据结构的基础。

图的遍历可以参考多叉树的DFS遍历框架

/* 多叉树遍历框架 */
void traverse(TreeNode* root) {
    if (root == nullptr) return;
    // 前序位置
    for (TreeNode* child : root->children) {
        traverse(child);
    }
    // 后序位置
}

图和多叉树最大的区别是，图是可能包含环的，你从图的某一个节点开始遍历，有可能走了一圈又回到这个节点，而树不会出现这种情况，从某个节点出发必然走到叶子节点，绝不可能回到它自身。

所以图如果包含环，需要一个visited数组进行辅助。 onPath 数组的操作很像回溯算法套路的做「做选择」和「撤销选择」，区别在于位置：回溯算法的「做选择」和「撤销选择」在 for 循环里面，而对 onPath 数组的操作在 for 循环外面。

// 记录被遍历过的节点
vector<bool> visited;
// 记录从起点到当前节点的路径
vector<bool> onPath;

/* 图遍历框架 */
void traverse(Graph graph, int s) {
    if (visited[s]) return;
    // 经过节点 s，标记为已遍历
    visited[s] = true;
    // 做选择：标记节点 s 在路径上
    onPath[s] = true;
    for (int neighbor : graph.neighbors(s)) {
        traverse(graph, neighbor);
    }
    // 撤销选择：节点 s 离开路径
    onPath[s] = false;
}

示例

来看力扣第 797 题「所有可能路径」，力扣

题目输入一幅有向无环图，这个图包含 n 个节点，标号为 0, 1, 2,..., n - 1，请你计算所有从节点 0 到节点 n - 1 的路径。

输入的这个 graph 其实就是「邻接表」表示的一幅图，graph[i] 存储这节点 i 的所有邻居节点。

比如输入 graph = [[1,2],[3],[3],[]]，就代表下面这幅图：

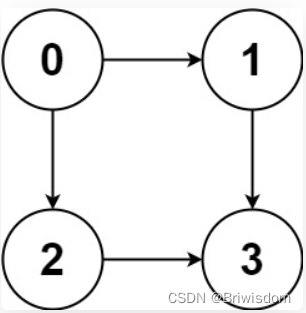
class Solution {
    // 记录所有路径
    vector<vector<int>> res;

public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        // 维护递归过程中经过的路径
        vector<int> path;
        traverse(graph, 0, path);
        return res;
    }

    /* 图的遍历框架 */
    void traverse(vector<vector<int>>& graph, int s, vector<int>& path) {
        // 添加节点 s 到路径
        path.push_back(s);

        int n = graph.size();
        if (s == n - 1) {
            // 到达终点
            res.push_back(path);
            // 可以在这直接 return，但要正确维护 path
            // path.pop_back();
            // return;
            // 不 return 也可以，因为图中不包含环，不会出现无限递归
        }

        // 递归每个相邻节点
        for (int v : graph[s]) {
            traverse(graph, v, path);
        }
        
        // 从路径移出节点 s
        path.pop_back();
    }
};

内容来源：图论基础及遍历算法 :: labuladong的算法小抄

查看全文

http://www.kler.cn/a/9898.html