一次性搞懂dBSPL、dBm、dBu、dBV、dBFS的区别!
相信学习音乐制作的同学在混音阶段经常会碰到各种关于声音的单位,其中最具代表性的可能就是分贝家族的单位了,如dBSPL、dBm、dBu、dBV、dBFS等。
那么,这些单位分别表示什么,又有什么区别呢?
描述声音信号强弱的单位:分贝(dB)
我们都知道,声音本质上是一种物理上的波,这种波传到我们的耳膜上引起耳膜的振动,然后转化为生物信号传递到我们的大脑,我们就听到了声音。
描述声音的指标有很多,如音高、音色、音量等等。其中,我们常见的“分贝(dB/decibel)”,就是用来描述声音信号的声强级的一个单位,在某些时候也可以近似地理解成描述声音大小的一个单位。
不过,值得注意的是,“分贝(dB)”这个单位其实是一种相对的概念,即它并不能像描述频率的“赫兹(Hz)”、描述质量的“克(g)”、描述长度的“米(m)”那样给出一个客观的量,而只能给出两个相同物理量的比值。
毕竟,“分贝(dB)”这个单位并不是声学领域的专属单位,其一开始是来源于长途电讯的计测的,后来才被应用在电工、无线电、力学、冲击振动、机械功率和声学等领域。
不带后缀的dB(dBSPL)
我们最常见的分贝家族的单位应该就是不带后缀的“dB”了,其完整形式应该是“dBSPL”,其后的“SPL”是“Sound Pressure Levels(声压级)”的缩写。
因此,我们可以看到,这个单位侧重的是声音的振动所产生的压强,即声压(单位为Pa)。声强级与声压的平方成正比,遵循I=(P^2)/Z的关系。其中,I为声强级,P为声压,Z为媒介的特性声阻,而Z又等于声速©和密度(ρ)的乘积。
前面我们提到了,分贝是一个比值。所以既然有与其成正比的值,那么相应地就有与其成反比的值。
这个成反比的值是人为规定的标准声压值。在dBSPL的语境下,则是人耳在1000Hz的频率下能听到的最小的声音的声压值,大小是
0.00002Pa。我们规定声压在这个值的时候声音信号的声强级为0dBSPL。
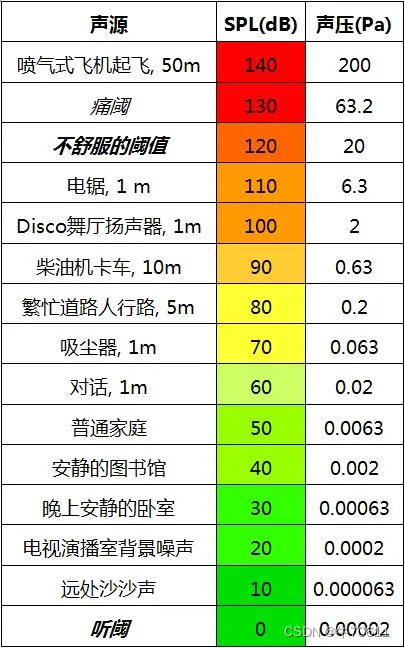
我们发现,如果仅仅只是具体的声压与这个标准声压的比值的话,那么得出的分贝值只能为正数,一些声压小于0.00002Pa的声音的分贝值也是正数,这显然不合理。
因此,在具体的公式中,我们还引入了对数:
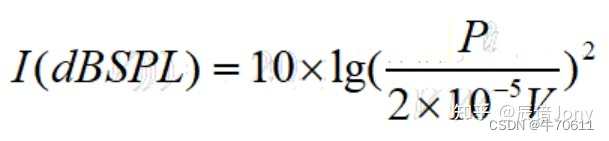
其中,I为声音信号的声强级,单位为dBSPL;P为我们具体测定的声压,单位为Pa。之所以这里有个平方,是因为前面提到了,声强和声压遵循I=(P^2)/Z的关系。
可以看出,这个公式直接计算出来的值是没有单位的,在这里我们人为地加上dBSPL的单位,简写为dB。
dBm、dBu、dBV
事实上,在分贝家族的单位里,只有dBSPL是与物质世界中的声波有直接关系的,剩下的单位都是间接地表示物质世界中的声音信号的声强级的。
其中,dBm、dBu、dBV这三个单位都是与电信号相关的,通过表示电信号的强度来间接反映声音信号的声强级。毕竟,现在的很多音频文件都是以数字信号的形式储存于电脑等电子设备中的。
与前面的dBSPL类似地,dBm的计算同样也涉及到一对单位相同的值的比值,一个是具体的测定值,一个是标准值。这里选取的测定值是声音的功率,而标准值则是0.001W这个标准功率值。
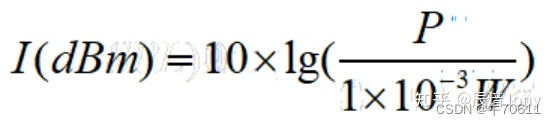
这里的这个“P”不再是压强了,而是功率了。同样,可以看出,这个公式直接计算出来的值也是没有单位的,在这里我们人为地加上dBm的单位。
dBu的计算跟dBm是一脉相承的,其选用的两个值分别是具体测定的电压值和标准电压值。这个标准电压值可以根据标准功率值和上世纪的标准电阻600Ω计算出来,约为0.7746V。dBu的公式为:
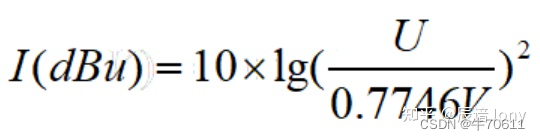
这里的“U”是具体测定的电压。对于这个公式直接计算出来的值,我们加上dBu的单位。这里之所以有二次方,是因为电阻一定时功率与电压的平方成正比。
接下来的dBV其实跟dBu是一类的,只是二者的标准电压值不同。计算dBV所用到的标准电压值为1V,这是在标准电阻为1000Ω的情况下计算出来的。dBV的公式为:
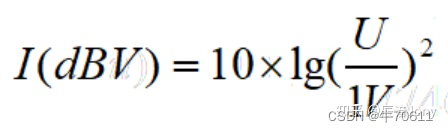
对于这个公式直接计算出来的值,我们加上dBV的单位。
dBFS
终于到了跟dBSPL、dBm、dBu、dBV都不同的dBFS了。如果说dBSPL、dBm、dBu、dBV这几个单位衡量的至少都是模拟信号的话,那么dBFS的对象就是纯数字信号了。
此外,dBFS与它们的一个很明显的区别就是,0dBFS是这个单位的标定最大值,所有超出0dBFS的值都属于异常情况。这个,通过观察dBFS的后缀“FS(Full Scale,满刻度)”也可以看出端倪。
宿主软件中常见的调音台上的电平的单位就是dBFS。我们可以观察到,这里的电平一般都是负数,偶尔电平呈正数的时候电平条就会变色,这就是提示你电平超过0dBFS了,需要进行调整。
一般来说,我们在宿主软件中新建工程的时候,往往都会提示我们选用采样精度,如16bit、24bit和32bit(float),而dBFS的计算在不同采样精度下也是不一样的。
拿16bit来举例。16bit的格式可记录的声音的动态范围为2的16次方也就是65536个单位。假设我们测定的某个音频的动态为D,如果想要将D的单位换算成dBFS,就需要运用到下面的这样一个公式:
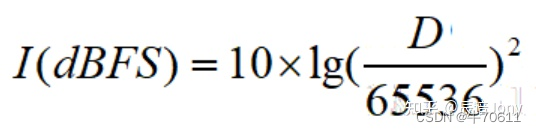
可以观察到,当D小于65536的时候,I总是为负的;当D等于65536的时候,I为0;而当I大于65536的时候,I大于0,属于异常情况。
另外,当D等于0,也就是没有电平的时候,I等于负无穷,这时电平的值也会变成“-∞”的记号。
以此类推,我们可以得到24bit下的dBFS的计算公式为:
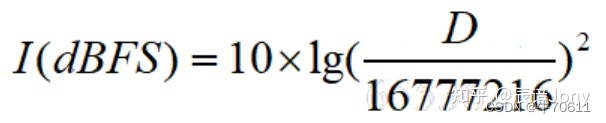
32bit下的dBFS的计算公式为:
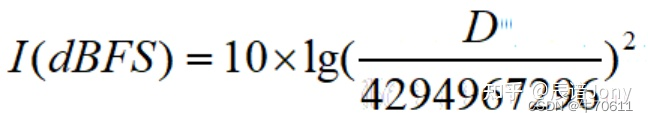
以上的这三个公式计算的结果都没有单位,我们人为地给结果加上dBFS的单位。
总结
最后,让我们简单地总结一下。分贝其实并不是一个表示声音大小的单位,其表示的是一对相同物理量的比值,其具体的值取决于被观测的物理量和相应的人为规定的基准值。
其中,dBSPL的被测量是声压,其基准值是0.00002Pa;dBm的被测量是功率,其基准值是0.001W;dBu的被测量是电压,其基准值是0.7746V;dBV的被测量也是电压,其基准值是1V。
与以上几个都不同,dBFS的被测量是数字音频领域的动态值,其基准值在不同采样精度下不同,16bit下是65536个单位,24bit下是16777216个单位,32bit下是4294967296个单位。
我们在生活中听人说的“分贝”一般指的是dBSPL,这个值可正可负,理论上来说没有上下限;在音乐制作中,我们最常遇见的“分贝”多数情况下指的是dBFS,这个值绝大多数情况下是负的,且有理论上限0dBFS。
