七大排序
排序的稳定性:两个相等的数据,如果经过排序后,排序算法能保证其相对位置不发生变化,则我们称该算法是具备稳定性的排序算法。
一、选择排序
1.直接选择排序(O(N^2) 不稳定排序)
原理:每次在一组待排序的数组中选择最大(最小)的一个元素,存放在无序区间的最后或最前,直到全部待排序元素排列完毕为止。
//直接选择排序
public static void selectionSort(int[] arr){
//每次从待排序数组中选择最小值,放在待排序数组的最前面
//已经有序的集合[0,i),待排序的集合[i+1,n)
//最外层的for循环代表的是要执行的总次数,当走到最后一趟时,数组已经有序
for (int i = 0; i < arr.length - 1; i++) {
//min存储了最小值元素的下标
int min = i;//让它从0开始,也就是i
//每次从待排序的数组中选择最小值
for (int j = i + 1; j < arr.length; j++) {
if(arr[j] < arr[min]){
min = j;
}
}
//此时min就存储了最小值元素的下标,就把min对应的元素换到无序区间的最前面
swap(arr,i,min);
}
}
private static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public static void main(String[] args) {
int[] data = {9,2,5,7,5,4,3,6};
SevenSort.selectionSort(data);
System.out.println(Arrays.toString(data));
}

直接选择排序是非稳定排序,例子中相等的两个5发生了位置交换。
1.1.双向选择排序
优化:之前的直接选择排序,每次只能从无序区间中选择一个元素,一趟下来只有一个元素到达了最终位置。现在每次从无序区间中选择一个最小值和一个最大值,分别放在数组的最前面和最后面,进行排序。
/**
* 双向选择排序
* @param arr
*/
public static void selectionSortOp(int[] arr){
int low = 0,high = arr.length - 1;
while (low <= high){
int min = low,max = low;//最大值和最小值都从最左侧开始
//有序区间[0,low),无序区间[low+1,high)
//在无序区间中继续找最大值最小值
for(int i = low + 1;i <= high;i ++){
if(arr[i] > arr[max]){
max = i;
}
if(arr[i] < arr[min]){
min = i;
}
}
swap(arr,low,min);
//特殊情况:当最大值出现在最左侧low的位置,则交换low会影响max
if(max == low){
max = min;
}
swap(arr,high,max);
low += 1;
high -= 1;
}
}
public static void main(String[] args) {
int[] data = {9,2,5,7,5,4,3,6};
SevenSort.selectionSortOp(data);
System.out.println(Arrays.toString(data));
}
2.堆排序(O(N*logN) 不稳定排序)
public static void heapSort(int[] arr) {
// 1.将任意数组调整为最大堆
// 从最后一个非叶子节点开始
for (int i = (arr.length - 1 - 1) / 2; i >= 0; i--) {
siftDown(arr,i,arr.length);
}
// 依次将堆顶元素和最后位置元素交换
// 最开始待排序数组[0...arr.length - 1] 已排序的数组[]
// 交换一个之后 [0...arr.length - 2] [arr.length- 1]
// 交换第二个值之后 [0..arr.length - 3] [arr.length - 2,arr.length - 1]
// 此处终止条件不用写i = 0 ,当整个待排序数组就剩一个元素时,其实整个数组已经有序
for (int i = arr.length - 1; i > 0; i--) {
swap(arr,0,i);
siftDown(arr,0,i);
}
}
/**
* 元素下沉操作
* @param arr
* @param i
* @param n 当前arr中有效的元素个数
*/
private static void siftDown(int[] arr, int i, int n) {
// 仍然存在子树
while ((2 * i) + 1 < n) {
int j = 2 * i + 1;
// 右孩子存在且大于左子树值
if (j + 1 < n && arr[j + 1] > arr[j]) {
j = j + 1;
}
// j对应的下标就是左右子树的最大值
if(arr[i] >= arr[j]) {
break;
}else {
swap(arr,i,j);
i = j;
}
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
二、插入排序
1.直接插入排序(O(N^2) 稳定排序)
原理:每次选择无序区间的第一个元素,插入到有序区间的合适位置,不断重复此流程,直到整个数组有序。
/**
* 直接插入排序
* @param arr
*/
public static void insertionSortBase(int[] arr){
//有序区间[0,i) [0,1),默认第一个元素是有序的
for (int i = 1; i < arr.length; i++) {
//无序区间[i,n)
for (int j = i; j > 0; j--) {
if(arr[j] < arr[j - 1]){
swap(arr,j,j - 1);
}else{
break;
}
}
}
}
1.1.折半插入排序
遍历原来的有序区间,由于找要插入的位置处于有序区间中,所以可以利用二分查找,来快速定位要插入的位置
public static void insertionSortBS(int[] arr){
//默认第一个元素有序
for(int i = 1;i < arr.length;i ++){
//无序区间的第一个值
int val = arr[i];
//有序区间:[0,i)
int low = 0;
int high = i;
while (low < high){
int mid = (low + high) / 2;
if(val >= arr[mid]){
low = mid + 1;
}else{
high = mid;//因为右区间取不到,所以不需要 -1
}
}
//进行数据搬移
for (int j = i; j > low; j--) {
arr[j] = arr[j - 1];
}
//low就是元素要插入的位置
arr[low] = val;
}
}
2.希尔排序(O(N^1.3) 不稳定排序)
选定一个整数gap,待排序的数据按gap分组,所有距离为gap的数据放一组,将组内元素进行排序,然后不断缩小gap的大小,直到变为1.当gap为1时整个数组近乎有序,直接调用普通排序即可。
一般gap就是不断地进行/2或者/3,直到等于1.

public static void shellSort(int[] arr){
int gap = arr.length >> 1;
while (gap > 1){
//不断按照gap分组,组内进行插入排序
insertionSortGap(arr,gap);
gap /= 2;
}
//整个数组进行插入排序
insertionSortGap(arr,1);
}
private static void insertionSortGap(int[] arr, int gap) {
//最外层从gap索引开始向前看,看的元素是距离它gap长度的元素
for (int i = gap; i < arr.length; i++) {
//j-gap>=0说明数组前面还有距离相同的元素,比较j位置元素和j-gap位置元素大小,确定是否要交换
for (int j = i; j - gap >= 0 && arr[j] < arr[j - gap]; j = j - gap) {
swap(arr,j,j- gap);
}
}
}
三、交换排序
1.冒泡排序(O(N^2) 稳定排序)
原理:就是相邻元素挨个比较,遇到比自己小的就交换,直到最后元素有序
/**
* 冒泡排序
* @param arr
*/
public static void bubbleSort(int[] arr){
//最外层控制的是要比较的趟数
for (int i = 0; i < arr.length - 1; i++) {
boolean flag = false;
for (int j = 0; j < arr.length - 1 - i; j++) {
if(arr[j] > arr[j + 1]){
swap(arr,j,j+1);
flag = true;
}
}
if(flag == false){
break;
}
}
}
2.快速排序(不稳定排序 O(N*logN))
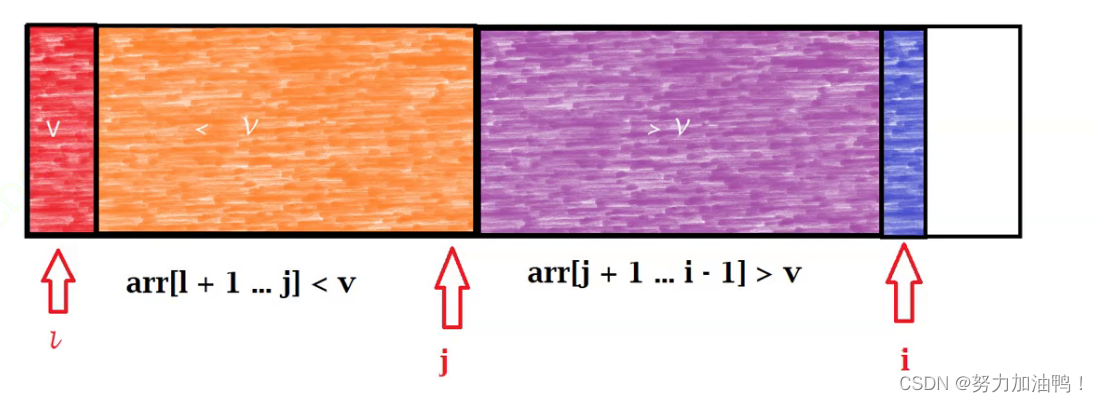
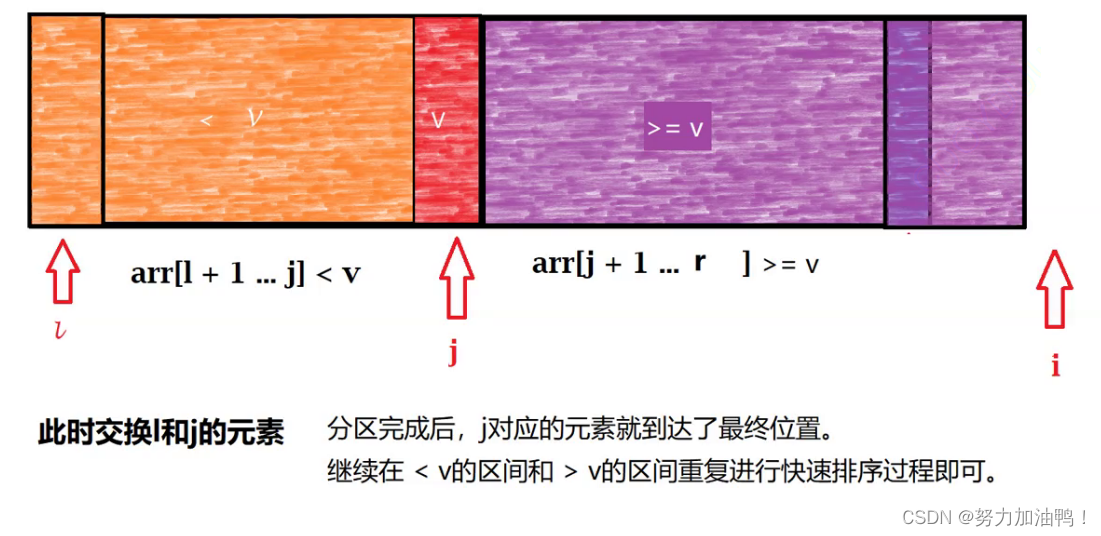
原理:选取一个区分点(基准值),将数组分为三部分,
基准值之前的数组<基准值<基准值之后的元素,接着重复快排的过程。

/**
* 快速排序的基本实现
* @param arr
*/
public static void quickSort(int[] arr){
quickSortInternal(arr,0,arr.length - 1);
}
/**
* 在l...r上进行快速排序
* @param arr
* @param l
* @param r
*/
private static void quickSortInternal(int[] arr, int l, int r) {
if(r - l <= 15){
//递归终止时,小数组使用插入排序
insertBase(arr,l,r);
return;
}
//选择基准值,找到该值对应的下标
int p = partition(arr,l,r);
//在小于基准值区间进行快速排序
quickSortInternal(arr,l,p - 1);
//在>=基准值的区间进行快速排序
quickSortInternal(arr,p + 1,r);
}
/**
* 在[l,r]上选择基准值,将数组划分为 < v 和 >= v两部分,返回基准值对应的下标
* @param arr
* @param l
* @param r
* @return
*/
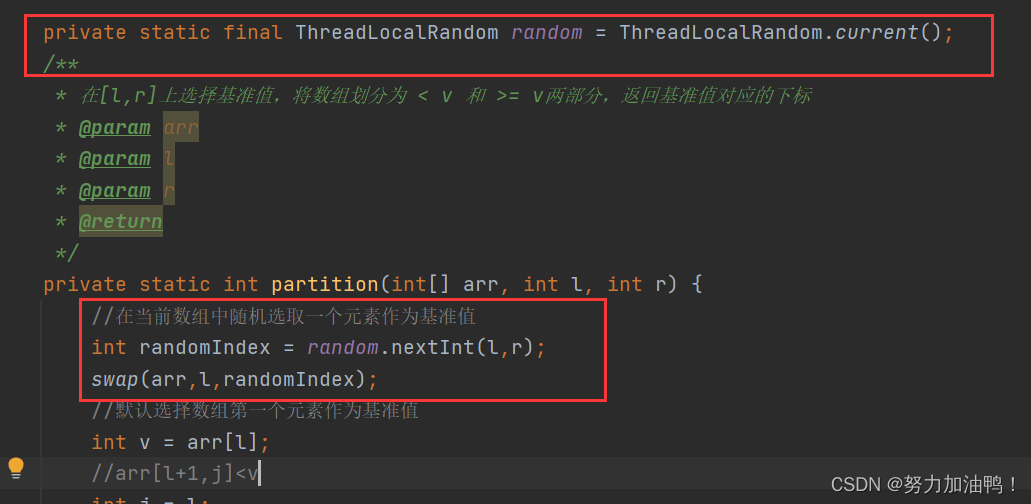
private static int partition(int[] arr, int l, int r) {
//默认选择数组第一个元素作为基准值
int v = arr[l];
//arr[l+1,j]<v
int j = l;
//i是当前处理元素的下标
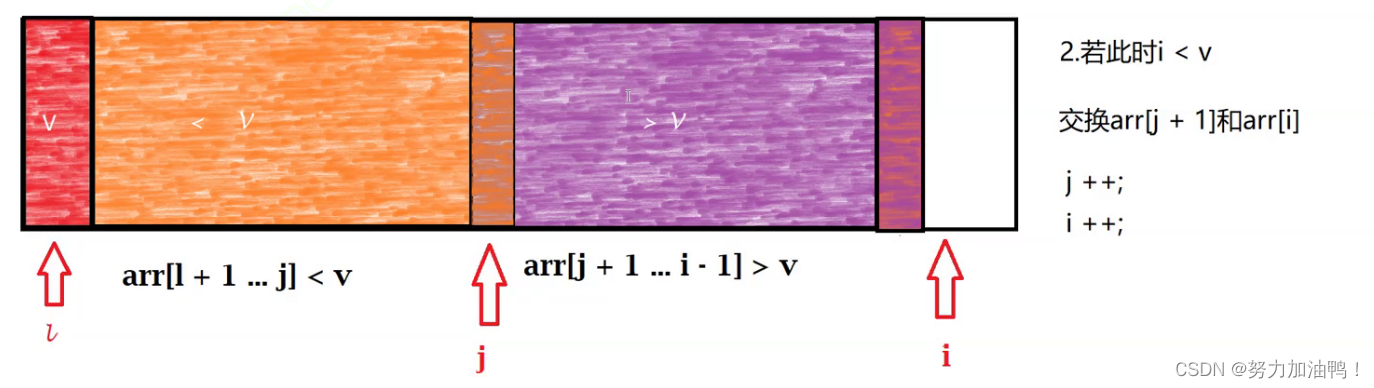
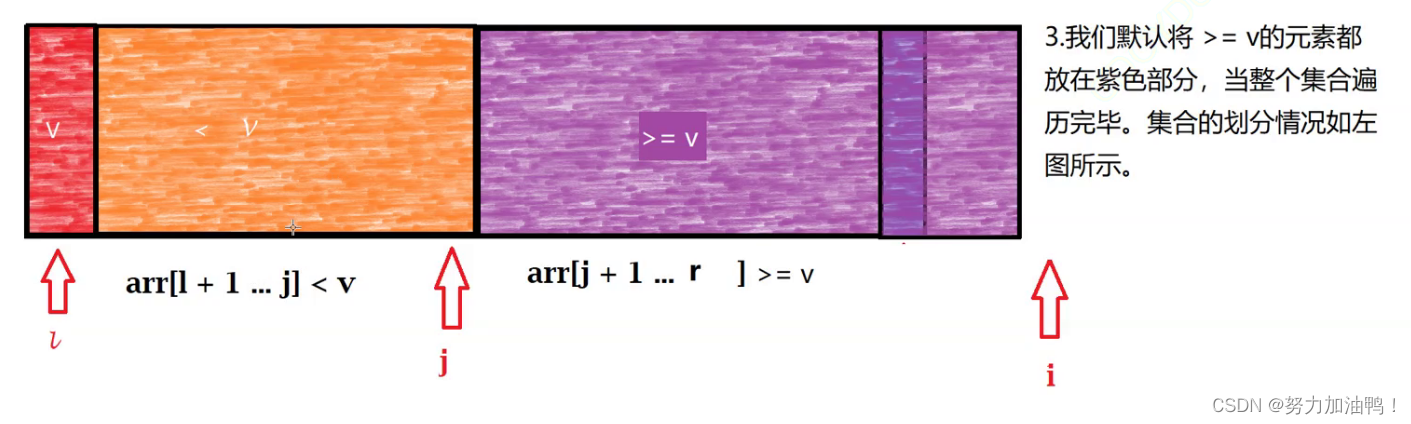
//arr[l + 1...j]<v arr[j+1...i]>=v
for (int i = l + 1; i <= r; i++) {
if(arr[i] < v){
swap(arr,j+1,i);
j ++;
}
}
swap(arr,l,j);
return j;
}
随机快排
四、归并排序(O(N*logN) 稳定排序)
分为两个小步骤:
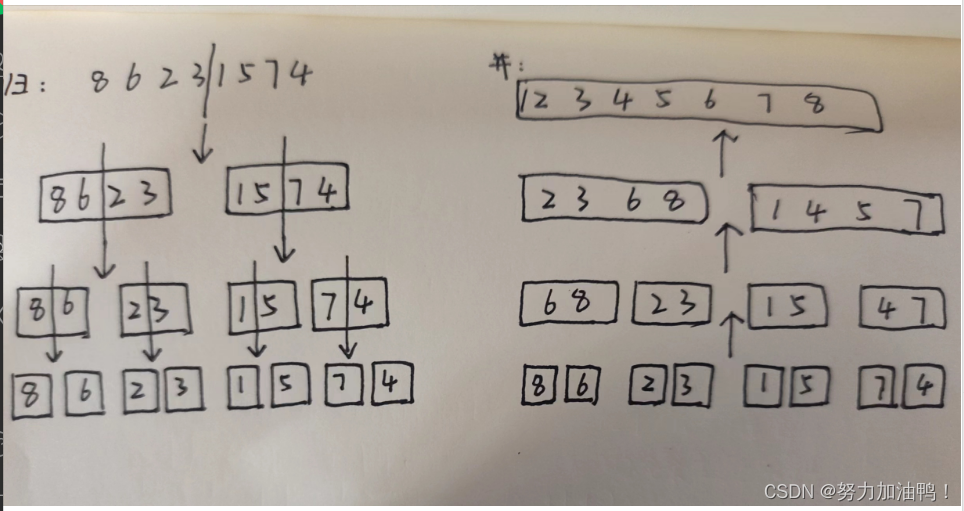
1.归:
将数组进行拆分,直到每个小数组只有一个元素为止
2.并:
将拆分的元素为1的小数组,相邻之间进行合并,合并的数组是有序的,最终合并为一个有序的大数组。
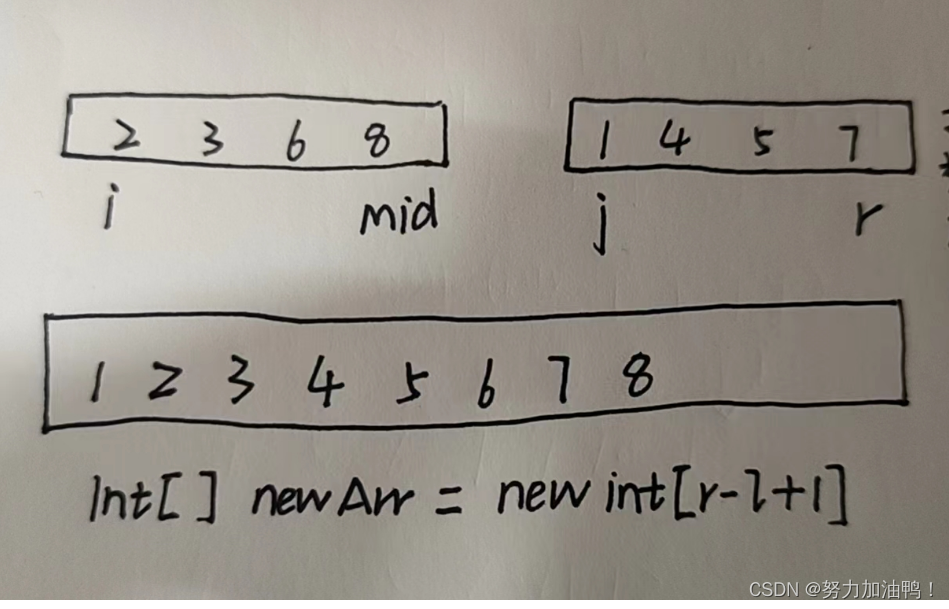
拆分数组是将原数组一分为二,数组左区间为l,右区间为r,左半区间[l,mid],右半区间[j,r],通过比较进行合并
合并时创建一个临时数组,大小就和合并后的数组大小相同。
/**
* 归并排序
* @param arr
*/
public static void mergeSort(int[] arr){
mergeSortInternal(arr,0,arr.length - 1);
}
private static void mergeSortInternal(int[] arr, int l, int r) {
if(l >= r){
//此时区间只剩下一个元素,不需要排序,直接返回
return;
}
int mid = l + ((r - l) >> 1);//当写为(l+r)>>1时会有溢出风险
//在拆分后的两个小数组上进行归并排序
mergeSortInternal(arr, l,mid);
mergeSortInternal(arr,mid+1,r);
//此时左半区间和右半区间都已经有序
//不是直接将两个区间进行合并,而是两个小区间之前存在乱序才进行合并
if(arr[mid] > arr[mid + 1]){
//arr[mid]<=arr[mid+1]此时整个区间已经有序,不需要merge操作
merge(arr,l,mid,r);
}
}
private static void merge(int[] arr, int l, int mid, int r) {
//开辟一个新数组,大小和合并后的数组大小相同
int[] temp = new int[r - l + 1];
//将新数组内容拷贝到原数组
for (int i = l; i <= r; i++) {
temp[i -l] = arr[i];//原数组arr是从0开始,而新数组是从l开始,有l个单位的偏移量
}
//遍历新数组,选择左半区间和右半区间最小值写回原数组,对原数组值进行覆盖
int i = l;
int j = mid + 1;
//k表示处理到原数组的哪个位置
for (int k = l; k <= r; k++) {
if(i > mid){
//此时左区间已经处理完毕,将右半区间所有剩余的元素写回原数组
arr[k] = temp[j - l];
j ++;
}else if(j > r){
arr[k] = temp[i - l];
i ++;
}else if(temp[i - l] <= temp[j - l]){
arr[k] = temp[i - l];
i ++;
}else{
arr[k] = temp[j - l];
j ++;
}
}
}
4.1归并排序的衍生问题
1.海量数据的处理
此时要排序的数据大小为100G,内存只有1G,如何将100G数据进行排序
a.先把100G的大文件拆分为200份,每份0.5G
b.分别对200份的0.5G的小文件进行内部排序(只要时间复杂度为Nlogn级别的排序算法都可以)
c.最后对200份小文件进行merge操作,最后大文件就有序了~
