当前位置：首页 > article >正文

力扣刷题笔记26——最小的k个数/快速排序学习/快排与冒泡的时间复杂度

article 2024/9/19 9:48:32

最小的k个数/快速排序学习/快排与冒泡的时间复杂度

问题
我的代码
示例代码
快速排序代码

问题

来自力扣：

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

示例 1：
输入：arr = [3,2,1], k = 2
输出：[1,2] 或者 [2,1]
示例 2：
输入：arr = [0,1,2,1], k = 1
输出：[0]
 

限制：
0 <= k <= arr.length <= 10000
0 <= arr[i] <= 10000

我的代码


#include <iostream>
using namespace std;
#include <algorithm>
#include <vector>
#include<queue>
#include <typeinfo>
#include <numeric>
#include<cmath>
#include<map>
#include<string>
#include<stack>
#include<utility>

class Solution {
public:
	vector<int> getLeastNumbers(vector<int>& arr, int k) {
		if (arr.size() == 0 || k == 0) {
			//vector<int> tmp;
			return {};
		}
		int nsize = arr.size();
		sort(arr.begin(), arr.end());
		vector<int> tmp;
		for (int i = 0; i < k; ++i) {
			tmp.push_back(arr[i]);
		}
		return tmp;
	}
};
int main() {
	Solution myso;
	vector<int> arr = {1,2,3};
	vector<int> nums = myso.getLeastNumbers(arr,1);
	for (auto num : nums) {
		cout << num<<"\t";
	}

	return 0;
}

做法：先排序，后输出。我本来自己用冒泡排序实现排序的，但是提交后报错了，说超时。可能是因为冒泡排序是O( $N^2$ )的时间复杂度。用了sort函数后，就没有报错。查了下，好像复杂度低，只有O( $Nlog_2N$ )。

示例代码

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        const int N=10005;
        vector<int> cnt(N);
        int mmax=-1;
        for(auto num:arr){
            cnt[num]+=1;
            mmax=max(mmax, num);
        }
        cnt.resize(mmax+1);
        vector<int> ans;
        ans.reserve(k);
        for(int i=0; k&&i<=N; i++){
            while(cnt[i]>0&&k){
                ans.push_back(i);
                k--;
                cnt[i]--;
            }
        }
        return ans;
    }
};

这个代码其实有点投机取巧，题目说值不会超过10000，所以它用了个数组，记录每种值出现了几次。然后把小的数值存进一个ans数组里，作为输出。这么做的好处就是，只需要对原数组进行一次循环遍历。坏处就是内存消耗较大。

快速排序代码

快速排序的思想：选定一个值p，然后把小于p的放v1，大于p的放v2。这样就得到了两个子数组v1和v2，其中v1的元素值都是小于v2。对v1再进行选值和排序，可以得到v1_1和v1_2。一直这样划分下去，就可以实现排序。
时间复杂度的证明看这个：快速排序时间复杂度分析
知乎有人给出了一个表格：
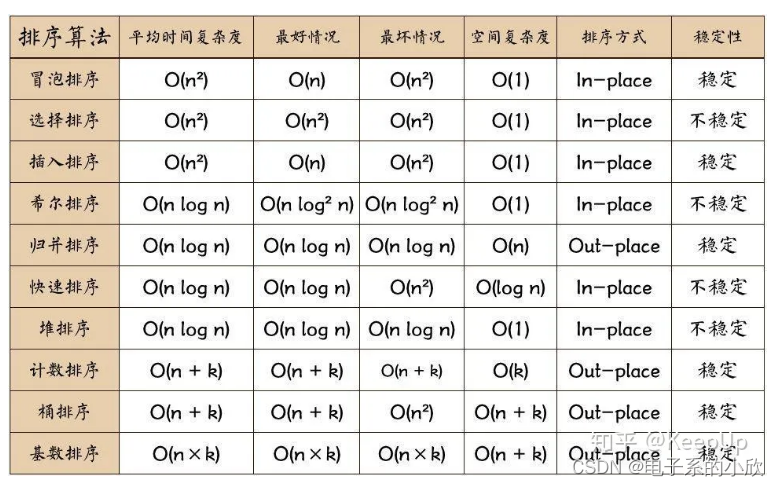
在这里插入图片描述
对于这道题，代码为这个：

class Solution {
    int partition(vector<int>& nums, int l, int r) {
        int pivot = nums[r];
        int i = l - 1;
        for (int j = l; j <= r - 1; ++j) {
            if (nums[j] <= pivot) {
                i = i + 1;
                swap(nums[i], nums[j]);
            }
        }
        swap(nums[i + 1], nums[r]);
        return i + 1;
    }

    // 基于随机的划分
    int randomized_partition(vector<int>& nums, int l, int r) {
        int i = rand() % (r - l + 1) + l;
        swap(nums[r], nums[i]);
        return partition(nums, l, r);
    }

    void randomized_selected(vector<int>& arr, int l, int r, int k) {
        if (l >= r) {
            return;
        }
        int pos = randomized_partition(arr, l, r);
        int num = pos - l + 1;
        if (k == num) {
            return;
        } else if (k < num) {
            randomized_selected(arr, l, pos - 1, k);
        } else {
            randomized_selected(arr, pos + 1, r, k - num);
        }
    }

public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        srand((unsigned)time(NULL));
        randomized_selected(arr, 0, (int)arr.size() - 1, k);
        vector<int> vec;
        for (int i = 0; i < k; ++i) {
            vec.push_back(arr[i]);
        }
        return vec;
    }
};