【MATLAB源码-第56期】基于WOA白鲸优化算法和PSO粒子群优化算法的三维路径规划对比。
操作环境:
MATLAB 2022a
1、算法描述
1.粒子群算法(Particle Swarm Optimization,简称PSO)是一种模拟鸟群觅食行为的启发式优化方法。以下是其详细描述:
基本思想:
鸟群在寻找食物时,每只鸟都会观察自己和其他鸟之间的距离,以及当前找到的食物的位置。每只鸟都会向自己历史上找到的最好食物位置和整个群体找到的最好食物位置飞翔。通过这种方式,鸟群可以在一定范围内快速找到食物。
算法流程:
1. 初始化:随机生成一个粒子群,每个粒子表示在解空间中的一个潜在解。
2. 评估:为每个粒子设定一个初始位置和速度,并计算它的适应度值。
3. 更新速度和位置:
- 对每个粒子,根据以下公式更新其速度:
\( v_{i} = wv_{i} + c_{1}r_{1}(pbest_{i} - x_{i}) + c_{2}r_{2}(gbest - x_{i}) \)
其中:
- \( v_{i} \) 是粒子i的速度。
- \( w \) 是惯性权重。
- \( c_{1}, c_{2} \) 是学习因子。
- \( r_{1}, r_{2} \) 是随机数。
- \( pbest_{i} \) 是粒子i的个人最佳位置。
- \( gbest \) 是全局最佳位置。
- \( x_{i} \) 是粒子i的当前位置。
- 更新粒子位置:\( x_{i} = x_{i} + v_{i} \)
4. 更新pbest和gbest:如果一个粒子在新位置得到更好的适应度值,更新其pbest。同样,如果群体中的任何粒子在新位置得到了更好的适应度值,更新gbest。
5. 终止条件:当满足特定的终止条件(如迭代次数或适应度达到预定阈值)时,算法结束,并返回gbest作为最佳解。
2.白鲸优化算法(Whale Optimization Algorithm, WOA)是一种模拟白鲸捕食行为的优化算法,由Mirjalili和Lewis于2016年提出。这种算法受到白鲸独特的捕食策略——螺旋式逼近猎物和围捕的启发。算法的基本思想是通过模拟白鲸的这两种捕食行为来寻找问题的最优解。
算法描述
初始化
算法开始时,随机生成一群白鲸个体,每个个体代表问题空间中的一个可能解。每个个体的位置由一个向量表示。
搜索猎物
白鲸通过两种策略搜索猎物(即寻找最优解):
1. 围捕策略:白鲸根据当前最优解的位置来更新自己的位置。这是通过以下公式来实现的:
\[ \vec{X}(t+1) = \vec{X}^*(t) - A \cdot D \]
\[ D = |\vec{C} \cdot \vec{X}^*(t) - \vec{X}(t)| \]
其中:
- \( \vec{X}(t+1) \) 是白鲸在下一时刻的位置。
- \( \vec{X}^*(t) \) 是当前最优解的位置。
- \( A \) 和 \( \vec{C} \) 是系数向量,控制着白鲸向最优解移动的强度和随机性。
- \( D \) 是当前白鲸位置与最优解之间的距离。
\( A \) 通常随着迭代次数的增加而减小,从而使得搜索过程从全局探索转变为局部开发。
2. **螺旋式逼近策略**:白鲸通过模拟螺旋运动来逼近猎物。这是通过以下公式来实现的:
\[ \vec{X}(t+1) = \vec{D}' \cdot \exp(b \cdot l) \cdot \cos(2 \pi l) + \vec{X}^*(t) \]
\[ \vec{D}' = |\vec{X}^*(t) - \vec{X}(t)| \]
其中:
- \( \vec{D}' \) 是当前白鲸位置与最优解之间的距离。
- \( b \) 是螺旋形状的常数。
- \( l \) 是一个随机数,控制螺旋的形状。
在每一次迭代中,算法以一定的概率选择使用围捕策略或螺旋式逼近策略来更新白鲸的位置。
更新最优解
在每一次迭代后,算法会评估所有白鲸个体的适应度值,并更新当前最优解。
终止条件
算法会持续进行迭代,直到达到预设的最大迭代次数或其他终止条件。
特点与应用
WOA算法具有简单、易实现、参数少等特点,已被广泛应用于各种优化问题中,如工程设计优化、经济负荷调度、图像处理等领域。它能够在全局和局部搜索之间进行有效的平衡,具有较好的优化性能。但是,像其他优化算法一样,WOA也可能会陷入局部最优解,因此有时需要与其他优化策略结合使用以提高其性能。
2、仿真结果演示
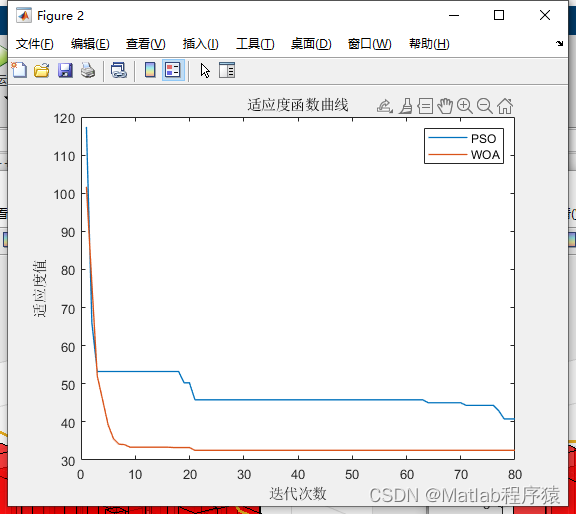
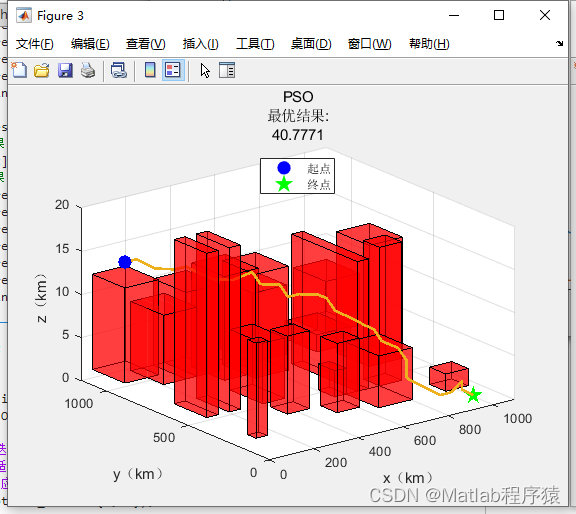
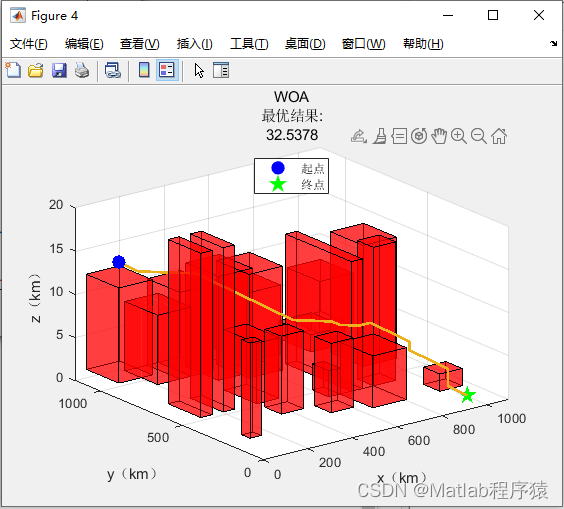
3、关键代码展示
略
4、MATLAB 源码获取
V
点击下方名片
