3.线性神经网络

#pic_center

$R_1$

$R^2$

知识框架

No.1 线性回归+基础优化算法

一、线性回归

线性回归是机器学习最基础的一个模型;也是我们理解之后所有深度学习模型的基础;所以我们从线性回归开始

1、买房案例

这个应用是说如何在美国买房;在美国买房;跟在任何地方买房都是一样;就说我们先得去看一下那个房;了解一下房子的各种信息;他可能跟很多地方不一样的地方在于是说我看中一个房之后;我要买它的话我是需要讲价;就是说举个例子;这里有一个房;这里显示它的基本信息是说;这个房的出价;售价是说大概550万美金;它有7个卧室5个卫生间;它的居住面积是4,865 square feed;折合大概是460平米的样子;但是呢;注意到这个价格它不是你的成交价;它是说我的卖房经纪人他的列价;那下面你可以看到是有一个;美国一个比较有名的卖房的网站;他对这个房子的估价是;大概是540十万的样子;但这两个价格都是给你做参考用的;你最终是说你得去出一个价格;所以这是一个预测问题;就说你得根据现在的行情得预测;说你大概多少钱能买下这个房子;

所以可以看到是说我给你的是标价;给你的是预计价格;然后呢我们要出一个价;这里是说;你的出价真的很重要;因为是真正的钱;我们再来看两套房子;

然后你的x轴是你的年份;然后呢这个曲线;这个曲线是说;根据历史信息你周围的房子;系统对你的评估价格;然后这一个dollar符号是说;你在此你在什么时候;出了多少钱买下了这个房子;所以你的最好的;当然是说;你的出的价格是远低于你的系统的估价;就说那你就赚到了这个房子还可以;就说就是他的估价跟;出价和估价是差不多的;

然后这一个其实就是我了;是我们第一次买房不懂那么多规矩;我们就多出了10万块钱;所以看到就是说;这个是;在一年之后;系统对这个房子的评估;仍然比我们的出价还要低一些;所以这个大概是10万美金的差价;所以呢从此以后我们就开始关心房价预测这个问题;

2、买房模型简化

接下来;我们通过这个应用来引出线性回归;这里我们做一个简化的模型;我们有做两个假设;第一个假设是说;影响房价的关键因素是三个;卧室的个数;卫生间的个数和居住面积;我们记为X1 X2 X3;其实你还有很多别的因素;我们先做一个最简单的假设;第二个假设是说我的成交价;是我关键因素的加权和;那就是说我的成交价y;就是W1乘以X1加上W2乘X2加上W3乘X3;再加上一个b;这里权重W1 W2 W3和偏差b;的实际值我们之后再来决定;

但是我们假设我们这些值已经有了;那么我们的成交价就是这四个项加和;这是我们的核心模型;

3、线性模型

那么把它拓展到一般化的线性模型;就是说;我们如果给定一个n维的输入x;它由x1一直到x n这n个项;然后我的线性模型呢;就会有一个n维的权重w;它包括了w1一直到w n;和一个标量的偏差b;那么我们的输出;就是我们的输入的加权和;就是从W1乘以X1一直加加加;加到w n乘x n;再加上偏差b;如果我们写成一个向量版本的话;那就是我的输入x一个向量和;权重w的累积;再加上我的标量偏差b;好这就是我的线性模型;

线性模型;之所以我们讲这个模型;是因为它可以看作是一个单层的;神经网络;假设我们的神经网络;通常我们用这样子的图来表示;我们的输入层;还有这里我们是画了n个输入的元素;跟我们机器的n;第一个输入元素;跟我们机器的n是匹配的;那就是说我有输入的维度是d;然后呢;我输出的维度是一就是一个O1;

然后每一个箭头代表了一个权重;这里我们没有画偏差;那就是说;我这个神经网络是一个输入层;和一个输出层;它之所以叫做单层神经网络;是因为它带权重的层就是1;我们可以把输出层不当做一个层;因为我把权重跟输入层放在一起;

4、神经网络

我们第一次提到神经网络;其实最早源于神经科学;在很在60年代50年代;大家对神经科学的一些突破;使得大家来学想;我是不是能够做一个人工的神经网络;来模拟人的大脑;这里显示的是一个;真实的神经元的构造;

可以看到是说我们的输入;这个神经元的输入需要挺多的;然后我们的输入之后;会在神经元这个地方发生一些计算;它的输出结果会通过一个;这个输出到下一个神经元;他的计算就表示说;你的输入是不是能够过了我的阈值;如果过了我的阈值;我就会发射一个神经信号出去;如果没有的话那我就是不发射;

这也是为什么我们把这一类的模型叫做神经网络;因为它来自于神经科学;但实际上来说;在过去几十年的50年60年的发展中;神经网络已经;远远的超出了神经科学所了解的范畴我们也不那么去追求;

5、损失函数

我们已经有了模型了我们可以做预测;那么接下来一个很重要的事情是说;我们要衡量我们的;预测的质量会怎么样;也就是说我们要比较我们真实的值;就是卖房的成交价和预估值;就是我对这个房子的估计;所以我们要比较他们的区别;

但是区别越小我的模型质量越高;区别越大我的模型质量就越差;所以我们假设y是我们的真实值;y hat是我们的估计值;有一个很常见的一个比较是说1/2乘以真实值减去估计值的平方;这叫平方损失;因为它衡量的是说我们没有完全猜中真实值所带来的损失;或者说是经济损失了;在已知所有个1/2;是因为我们只有求导的时候;可以很方便的把它消去;

6、训练数据

定了模型;定了损失之后;我们就来学习我们的参数了;这是我们的权重和我们的偏差;我们怎么学习呢;我们是集数据来学习的;我们一般来说会先收集一些数据点;来训练我们的模型;例如说这个例子里面;我们可以去采集;过去6个月里面所有卖的房子;他的房子的信息和他的最终的成交价;这些数据我们一般会称之为训练数据;是用来训练我们模型的数据;通常来说是越多越好了;但实际上来说你会受限于很多事情;比如说这个世界上就那么多房子;每个月卖的房子;他其实是一个缓慢的;可能是在增加可能是减少的过程;但他不会有无穷多的房子;所以的话;我们就算把所有的房子的信息;采集下来;也可能就那么多;所以一般来说我们有很多技术来处理;当你的数据不够的时候会怎么办;我们之后会有非常多的算法来;探讨这个问题;这里我们先不再深入了解;我们先来看一下训练样本;假设我们有n个样本的话;那我们可以把它;假设我们一个样本;每一个x是一个列的相量的话;我们一排一排排好;然后作为转置;那我们的大x的每一行;对应的就是一个样本;的y同样的它是一个列项量;那也是有n个样本;每一个y i就是一个实数的数值;这就是我们的x和y;也就是我们的数据;

7、参数学习

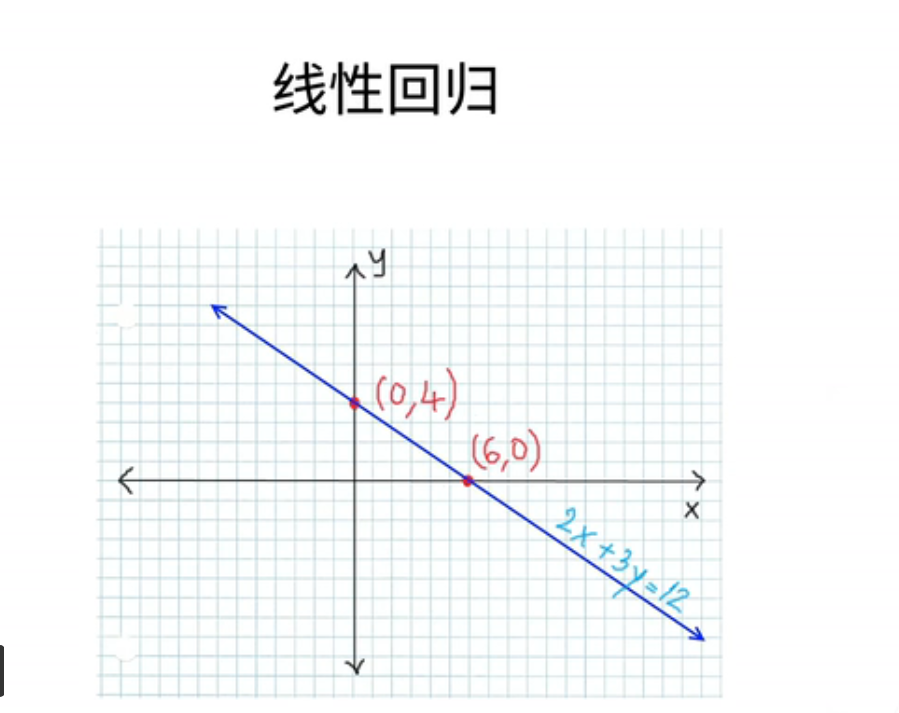
那么我们就可以求解我们的模型了;我们的怎么根据我们之前的损失;给定我们的数据;那么我们来评估说对于我们的模型;在每一个数据上的损失求均值;就会得到我们的一个损失函数;我们把它写出来;就是说它是关于我们的数据;x和y关于我们的权重;关于我们的偏差;它可以写开;就是说;1/2这个像来自于我们的损失函数;n分之一就是我们要求平均;然后呢对于每一个样本;我们的真实YI;减去后面是我们的预测值;就是;一i个样本的x和我们的权重的累积;和我们的偏差;当然我们可以写成一个向量版本;就是一个y向量版本的y减去;矩阵x乘以向量w再减去b;b是一个标量;然后对向量求l to no;这就是我们的损失函数;那我们的目标呢;就是说我们要找到一个w和一个b;使得我们的整个这一项的值最小;也就是说;我们可以最小我们的损失函数;来学习参数;我们选取一个WB;使得能最小化这一项;把这个最小化的它做为我们的解;也就是w和b;好这个整个就是我们的求解过程;

8、显示解

线性模型了;所以它是有显示解的;我们来看一下它的显示解;长成什么样子;;我们最简单是说因为我们有偏差;我们先把偏差加入我们的权重;使得我们的写起来方便一点;具体怎么加呢;就是我们加入一列特征全1的特征;加进我们的x里面;让我们再把偏差放到权重的最后面;放到我们的w里面;那么我们的预测就是x乘以w了;那我们的损失函数可以写成;2 n分之一;然后y减去x是w它的l作弄;

回忆下我们之前介绍的;矩阵计算里面我们可以对它来;展开求导;就是大家也回忆一下;我们是讲过这个例子的;它就是等于1/2;y减去x w;也就是我们的预计的一个偏差;再转置乘以x;因为这是线性模型;所以它的损失是一个凸函数;我们并没有解释什么是凸函数;你可认为就是一个比较简单的一个这样子的函数;

所以呢突函数它的性质是说;它的最有解是满足于一定是;使得它的t do等于0的地方;所以我们把它带进去;最后会得到是说我们的最优解w*;其实可以计算成为x转置乘以x;然后再求逆;再乘以x再乘以y;这是我们最优解的形式;当然是说;这个是我们;唯一的一个有最优解的模型;我们之后所有的解都不会有最优解了;

9、总结

线性回归;是对n维输入的一个加权和;再加上一个偏差;这是它的对一个输出值的预估;然后对于;他跟预测值和真实值距的差异;通常是用平方损失来衡量;

线性回归是有一个;是一个非常特别的一个模型;它有显示解;我们;这堂课所有别的模型都没有显示解;因为有显示解的模型;一般来说过于简单；机器学习通常是用来解决;NP难的问题;如果你一个模型可以很快求解的话;通常来说它的复杂度有限;难于衡量特别复杂的数据和复杂的是应用;所以来说我们一般不会再去追求显示解;

最后的话;我们之所以解释线性回归;是因为线性回归;确实是可以看作是一个单层的神经网络它是最简单的一种神经网络;好我们线性回归就介绍到这里;

二、 基础优化算法

在我们提供线性回归的实现之前;我们先来很简单的介绍一下优化方法;我们在接下来会有一大章的内容;来解释各种不一样的优化方法;但是我们在这里;先给大家做一个直观上的理解

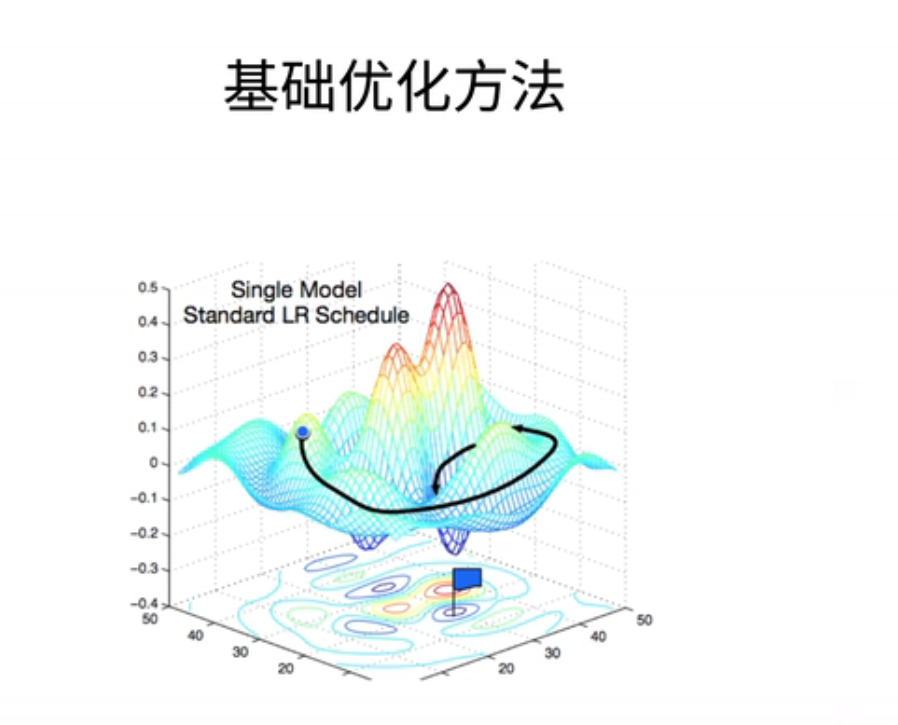
1、梯度下降

最常见的算法叫做梯度下降;就是说当我一个模型没有显示解的时候;我怎么办呢;我的一个做法是说;我首先挑选一个参数的随机初始值;可以随便在什么地方都没关系;然后呢我们记为W0;在接下来的时刻里面;我们不断的去更新W0;使得它接近我们的最优解;

具体来说我们的更新法则是这样子的;WT;它等于上一个时刻W(t-1)减去一个at;这是一个标量和损失函数;关于W(t-1)处的梯度;好这有两个项;第一个是它的梯度;第二个是它的学习率;这就a它;

我们来直观上解释下这是什么意思;我们来看一下这个图;这是一个很简单的二次函数的一个等高图;这个最优点在这个地方这是最小值;外面是最大值;如果看过地图的话也就是一个;每一个圈就是函数值等于一个固定值;同样值的一条曲线;

那么假设我们的W0是取在;这个地方的话;就是一般来说是随机取在一个地方;那么我们记得我们解释过它的梯度;也就是;使得这个函数的值增加最快的方向;那么它的负梯度就是它的;值下降最快的方向就是比如说这个黄线的方向;那么就是;负的这个梯度的值就是指向这个方向;接下来学习率就是;它代表是说我沿着这个方向;每一次走多远;比如说这个地方我走了大概那么远;然后把这个两个就说这一个;整个这一向就代表是这一条;这个点到这个点之间的向量;好我们把W0和这个相邻;加就可以拉得到W1的位置;同样的话在W1处;我们继续计算它的梯度;那就是在这个点上梯度;函数值下降最快的方向;然后我再沿着它再走一步;

就是你可认为我去爬山的时候;我可以不走大路对吧;我可以每一次沿着最陡的那条路;一直一直走下去;那我可以走到山顶;这就是梯度下降的一个直观解释;所以这里面学习率就是步长;它是一个叫做超参数的东西;超参数的话它一叫做hyperprameter;它就是一个我们需要;人为来指定的一个值;

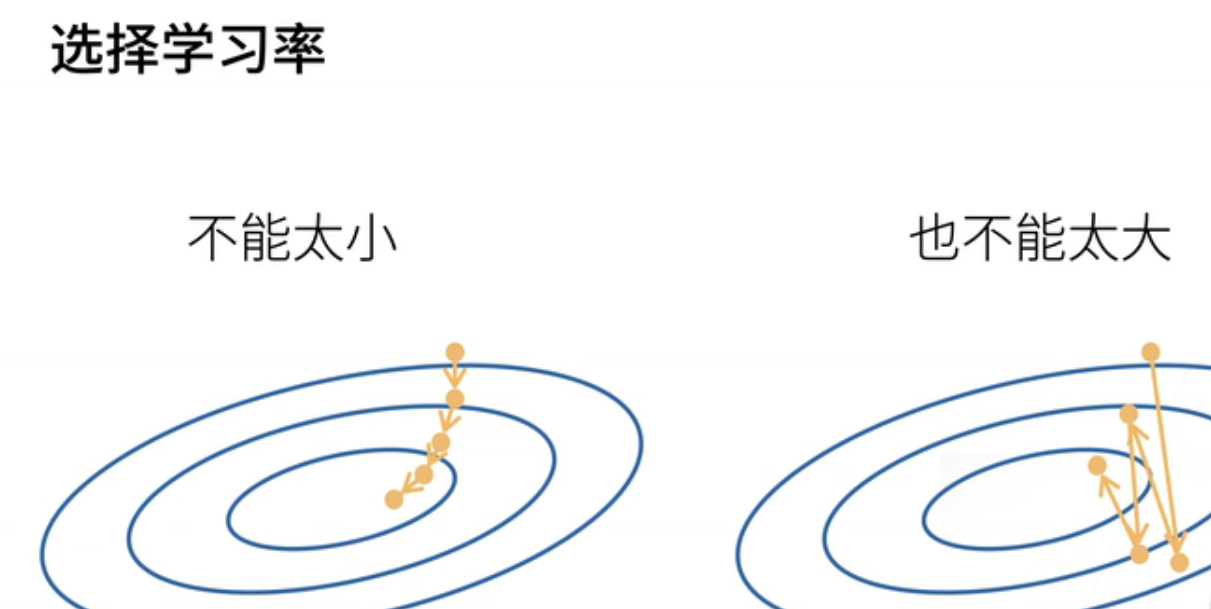
2、学习率

首先我们不能选太小;就说如果选太小的话;那么每一次走的步长很有限;我们到达一个点;我们需要走非常非常多的步骤;这个不是一件很好的事情;这是因为计算梯度是一件很贵的事情;我们之前有讲过;在自动求导里面说过;计算梯度和;是一件基本上是我们;整个模型训练里面最贵的那一个部分;所以我们尽量的要少来计算梯度;但是反过来讲我们也不能走太大;为什么是因为;比如说;我们这个地方一下子步子迈太大了;就迈过了我们在下降的地方;迈到了很远的地方;使得我们一直在震荡;并没有真正的在下降;所以就是说我们学习率不能太大;也不能太小;我们接下来会有一系列的教程教大家怎么选取合适的学习率

3、小批量随机梯度下降

在实际中我们很少直接使用梯度下降;;深度学习最常见的梯度下降版本叫做;小批量随机梯度下降;这是因为述说梯度下降里面;我们每次计算梯度;要对整个损失函数求导;这个损失函数;是对我们所有的样本的一个;平均损失;

所以这意味着是说求一次梯度;我们要把整个样本给你重新算一遍;这个是很贵的一件事情;它可能需要数分钟或者数个小时;一般来说;我们需要可能走个几百步;或者几千步的样子;这样子我们的计算代价太大了;那么一个近似的办法怎么做呢;就是我可以回忆一下我的损失;就是我们所有的样本的;损失的平均;那么我们近似他的话;我们可以随机采样第一个样本;用他的损失的平均;来近似于整个样本集上的损失的平均;当你的b很大的时候;这个近似当然很精确;当你b等于小的时候;它的近似不那么精确;但是b你很小的时候计算它的梯度;那就是比较容易;因为梯度的计算复杂度是跟样本的;个数是线性相关的;所以这里又叫做批量大小;是另外一个重要的超参数;

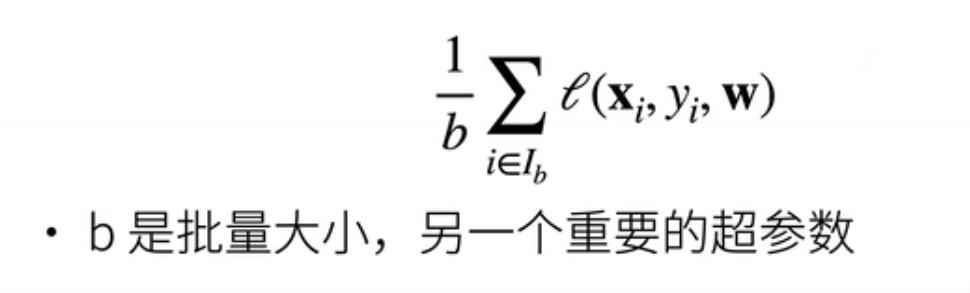
4、批量大小

批量大小不能太大;也不能太小;如果你太小的话;一个问题是说;我每次就算那么几个样本的梯度;很难以定型;之后我们会利用GPU来做计算;GPU的话动不动就上百上千个核;当你批量太小那就是计算不好;很大很好利用;但你也不能太大;太大的话;内存;跟你的批量大小很多时候是成正比的;所以你的特别是用GPU的话;内存是一个呃很大的一个瓶颈;因为你可能就那么16GB或者32GB的内存;接下来是说你也可能会浪费计算;举一个极端的例子;所有的样本都是一样的话;那么你不管批量大小多大;你用一个样本计算剃度;还是用10个还是用100个;计算的效果都是一样的;所以的话;假设你一个批量里面;存在着大量的差不多的样本的时候;那么呢你就在很多时候浪费了计算了;所以不要太大;

5、总结

总结一下就是说;梯度下降;就是不断的沿着梯度的反方向来;更新我们的模型;求解它的好处是说;我不需要有知道这个显示解什么样子;我只要不断的知道怎么求导数就行了;我们知道在自动求导那一章;我们讲过说;我给你一个函数;给你一个模型;我的深度学习框架;是能够帮你自动求导的;所以的话这一块就是做的比较简单了;

另外一个是说;小批量随机梯度下降;是深度学习默认的求解方法;虽然我们还有更好的算法;但是呢一般来说它是最稳定的;而且是最简单的;所以我们通常使用它;其中小批量随机梯度下降;里面有两个重要的超参数；一个是批量的大小;一个是学习率;我们待会在今后给大家解释;如何选择合适的批量大小;和学习率;这就是非常简单的优化算法的介绍;当然;优化算法是一个非常大的一个方向;我们会有可能会有几节课专门来讨论更好的更稳定的一些算法;但是;知道这个最简单版本已经在接下来的几个星期里面我们先是够用了;

三、 线性回归的从零开始实现

1、D2L注意点

来实现我们所有;讲过的算法和一些技术细节;这样的好处是说;可以帮助大家从很底层的地方;了解每一个模块;具体是怎么实现的

四、线性回归的简洁实现

五、QA

No.2 Softmax回归+损失函数+图片分类数据集

一、Softmax回归

二、损失函数

三、图片分类数据集

四、Softmax回归从零开始

五、Softmax回归简单实现

六、QA