CTF-Crypto学习记录-第四天 “ “ --- SHA1安全散列算法，实现原理。

前言

MD5学习MD5加密算法

SHA-1加密算法介绍

SHA-1（Secure Hash Algorithm1，安全散列算法1）是一种密码散列函数。
SHA-1可以生成一个被称为消息摘要的160位（20字节）散列值，散列值通常的呈现形式为40个十六进制数。

SHA-1的历史：

2005年，密码分析人员发现了对SHA-1的有效攻击方法，这表明该算法可能不够安全，不能继续使用，自2010年以来，许多组织建议用SHA-2或SHA-3来替换SHA-1。Microsoft、Google以及Mozilla都宣布，它们旗下的浏览器将在2017年停止接受使用SHA-1算法签名的SSL证书。
2017年2月23日，CWI Amsterdam与Google宣布了一个成功的SHA-1碰撞攻击，发布了两份内容不同但SHA-1散列值相同的PDF文件作为概念证明。
2020年，针对SHA-1的选择前缀冲突攻击已经实际可行。建议尽可能用SHA-2或SHA-3取代SHA-1。

关于SHA-1和MD5

在上一篇学习笔记里学了MD5加密算法，SHA-1和MD5同样是哈希函数，俩者对于任意长度明文的预处理也都是相同的，那么俩者有什么不同呢？

• 摘要长度 （安全性）
  SHA-1所产生的摘要是160位比MD5产生的摘要长32位，因此在安全性上SHA-1高于MD5。
• 运算速度
  同样因为，SHA-1的摘要长于MD5，运算步骤也比MD5多了16步，因此运算速度要慢于MD5

关于MD5和SHA-1，在如今现代计算环境中都已经不再被认为是安全的哈希函数了，为了保证数据和应用的安全，应该使用SHA-256或SHA-3等算法。

SHA-1 加密过程

同MD5一样，可以分为三个过程：

原文处理

对于任意长度明文，需要先进行填充处理，使得明文长度为448（mod 512）位，有俩种情况：

• 原始明文长度mod512不为448，需要进行填充；这里假设原始明文一共有b bit，那就在b+1 bit处填充一个1，后面全部填充0，直到明文长度mod512等于448为止。
• 第二种情况，原始明文长度mod512正好为448，这种情况也需要进行填充，总共填充512位的数据，直到明文再次mod512等于448为止。

因此填充的数据长度最小为1 bit ，最大为512 bit。‘
’
再得到448bit长度的明文后，还需要添加64bit的数据，使得明文长度等于512 bit。

填充处理完成之后是分组处理：

要先将恰好为512整数倍的明文，分成 L 个512 bit长度 的明文分组。接下来对每个512 bit大小的明文分组进行类似于MD5的操作；

• 先将512 bit 的明文分组，分成 16个 32 bit的子明文分组。可以用 M[k] 表示
• 之后再将这16个子明文分组扩展到 80个子明文分组。 可以用W[k]表示
  扩充的方式如下：

W t = M t , 当0≤t≤15
W t = ( W t-3 ⊕ W t-8⊕ W t-14⊕ W t-16 ) <<< 1, 当16≤t≤79

设置初始值和数据结构定义

一些相关定义：

SHA 1 针对输入的比特流是按块 (block) 依次进行处理的, 每个块的长度固定为 512 bit, SHA 1 算法允许的最大输入长度为 2^64−1 bit, 在 SHA 1 算法中, 我们将 32 bit 定义为字 (word), 所以每个字可以用 8 位十六进制来表示, 例如对于字 1010 0001 0000 0011 1111 1110 0010 0011 可表示为 A103FE23, 对于一个长度在 [0, 2^32−1] 的整数便可以用一个字来表示, 整数的最低有效 4 位为字的最右侧的十六进制字符, 对于一个整数 z, 若 0≤z<2^64 则 z=(2^32*x+y), 其中 0≤x,y<2^32, 于是 x, y都分别可以用一个字来表示, 我们记这两个字分别为 X, Y, 此时整数 z 便可以使用这对字来表示, 我们记为 (X,Y)

可以将针对bit 的逻辑运算符扩展定义到字上；

X AND Y 为两个字按位逻辑与
X OR Y 为两个字按位逻辑或
X XOR Y 为两个字按位异或
NOT X 为对字 X 的每一位按位取反

除了逻辑运算符，还可以定义字上的算术运算，

X + Y 定义为 (x + y) mod 2^32

最后定义字上的循环左移运算符（逻辑移位），循环左移即是将字的比特整体向左移动 n 位, 左侧溢出的比特位补到右侧空出来的比特位, 我们将这一运算记作 S^n(X), 循环左移可以使用逻辑表达式来描述, 如下所示：

S^n(X) = (X << n) OR (X >> 32 -n)

MD5中有4个初始变量值，而SHA-1中有五个链接变量，如下：

H0=0x67452301

H1=0xEFCDAB89

H2=0x98BADCFE

H3=0x10325476

H4=0xC3D2E1F0

此外 SHA-1定义了4个逻辑函数和4个常量。每个逻辑函数针对3个字作为输入，函数的输出为一个字，其中 t (0 ≤ t ≤ 79) 是变量, 函数的表达式如下：

  f(t;B,C,D) = (B AND C) OR ((NOT B) AND D)         ( 0 <= t <= 19)

  f(t;B,C,D) = B XOR C XOR D                        (20 <= t <= 39)

  f(t;B,C,D) = (B AND C) OR (B AND D) OR (C AND D)  (40 <= t <= 59)

  f(t;B,C,D) = B XOR C XOR D                        (60 <= t <= 79)

4个常量分别如下（十六进制表示）：

 K(t) = 5A827999         ( 0 <= t <= 19)

  K(t) = 6ED9EBA1         (20 <= t <= 39)

  K(t) = 8F1BBCDC         (40 <= t <= 59)

  K(t) = CA62C1D6         (60 <= t <= 79)

加密运算原理过程

SHA1有4轮运算，每一轮包括20个步骤，一共80步。

下图是 SHA-1算法中的一个回圈；

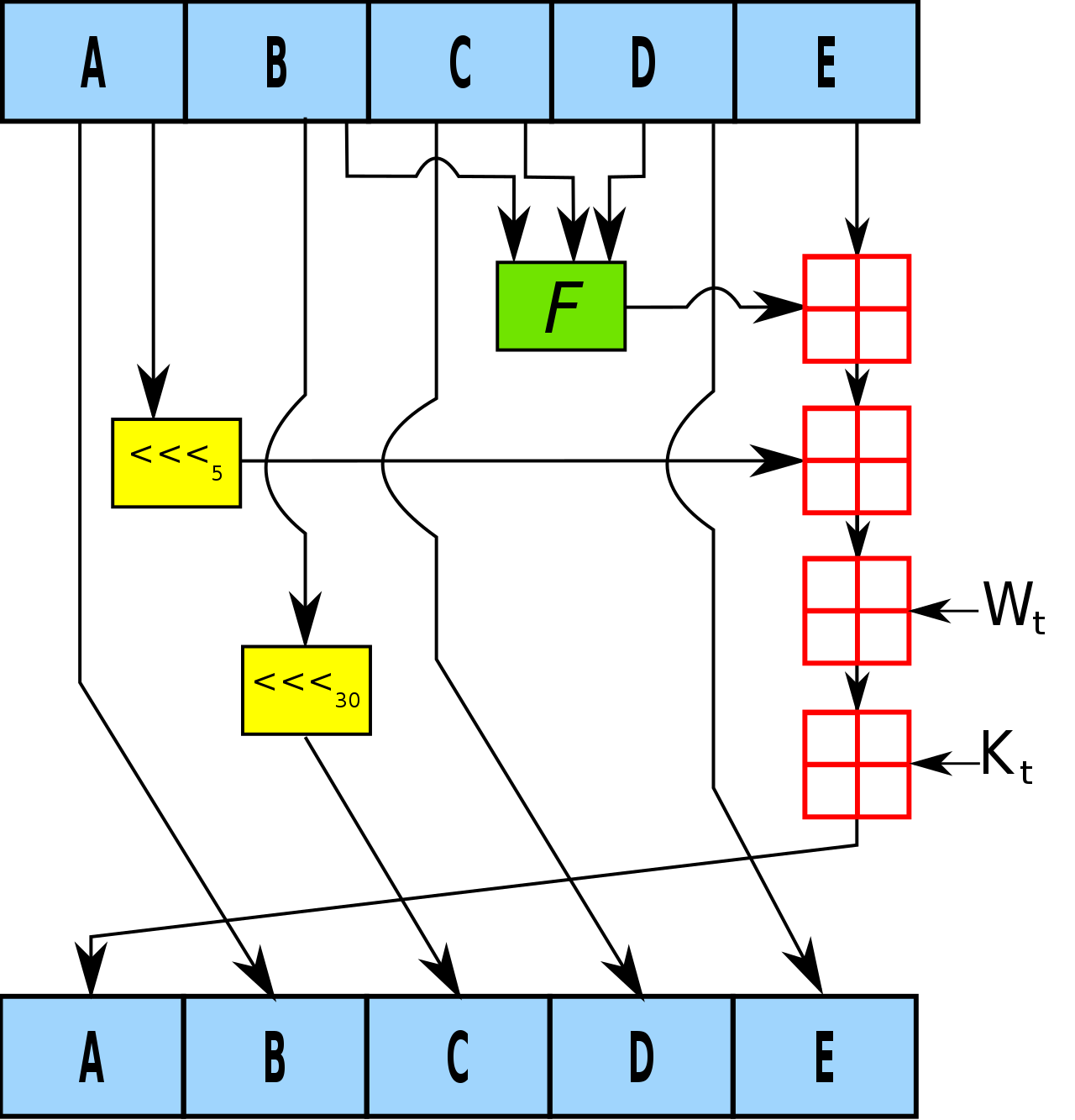
• 也如MD5一样，SHA-1会现将H0,H1,H2,H3,H4,H5五个初始变量依次放入ABCDE中；即 A = H0, B = H1, C = H2, D = H3, E = H4
• 定义循环变量 t, 对 t 从 0 到 79 依次赋值, 每一次循环执行如下操作：
  • TEMP = S^5(A) + f(t;B,C,D) + E + W(t) + K(t);
  • E = D;
  • D = C;
  • C = S^30(B);
  • B = A;
  • A = TEMP;
• 分别令 H0 = H0 + A, H1 = H1 + B, H2 = H2 + C, H3 = H3 + D, H4 = H4 + E

从 M(0) 开始每一轮计算后会得到新的 H0, H1, … , H4, 下一轮计算中使用上一次产生的新值, 对最后一个块计算完毕后得到的 H0, H1, … , H4便是算法的输出, 即原文的 SHA 1 哈希值

在python中调用SHA-1

import hashlib

# 要哈希的数据
data = b'Hello, World!'  # 在 Python 3 中，请确保数据以字节字符串的形式表示

# 创建一个 SHA-1 哈希对象
sha1 = hashlib.sha1()

# 更新哈希对象以处理数据
sha1.update(data)

# 获取 SHA-1 哈希值的十六进制表示
sha1_hash = sha1.hexdigest()

print("SHA-1 哈希值:", sha1_hash)

输出：

SHA-1 哈希值: 0a0a9f2a6772942557ab5355d76af442f8f65e01

文献参考：

https://www.cnblogs.com/scu-cjx/p/6878853.html
https://sunyunqiang.com/blog/sha1/
https://zh.wikipedia.org/zh-hans/SHA-1