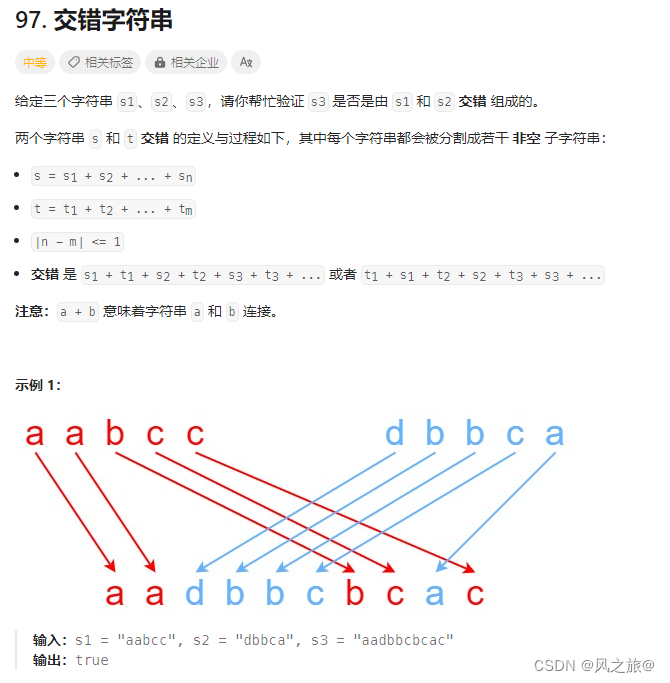
97. 交错字符串

题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

解题思路：动态规划。

1. 如果s1.length()+s2.length != s3.length()，直接返回false，否则使用动态规划求解。
2. 定义状态：dp[i][i]，表示s3的前i+j个字符是否由 s1的前 i 和字符和s2的前j个字符交错组成
3. 初始状态：dp[0][0]，显然当s1，s2，s3都为空时，dp[0][0]=true
4. 状态转移：对于dp[i][j]：判断 s 的第 i+j 个字符即 s[i + j -1]是由 s1[i-1] 匹配还是 s2[j-1] 匹配(索引从开始) 
   1. 如果 i >0：如果由s1[i-1]匹配，即 s3[i + j -1] == s1[ i-1] 并且 dp[i-1][j] = true时，dp[i][j] = true
   2. 如果 j >0：如果由s2[j-1]匹配，即 s3[i + j -1] == s2[ j-1] 并且 dp[i][j-1] = true时，dp[i][j] = true
5. 因为可以连续使用s1中的字符进行匹配，也可以连续使用s2中的字符进行匹配，索引对于 dp[i][j]的求解，需要从0开始从前往后进行遍历，只要有一个符合，dp[i][j] = true

AC代码

class Solution {
   public static boolean isInterleave(String s1, String s2, String s3) {
        if (s1.length() + s2.length() != s3.length()) {
            return false;
        }
        if (s1.length() == 0 || s2.length() == 0) {
            return s3.equals(s1) || s3.equals(s2);
        }
        boolean[][] dp = new boolean[s1.length() + 1][s2.length() + 1];
        dp[0][0]=true;
        for (int i = 0; i <= s1.length(); i++) {
            for (int j = 0; j <= s2.length(); j++) {
                if (i > 0) {
                    dp[i][j] |= dp[i - 1][j] && s1.charAt(i-1) == s3.charAt(i + j - 1);
                }
                if (j > 0) {
                    dp[i][j] |= dp[i][j - 1] && s2.charAt(j-1) == s3.charAt(i + j - 1);
                }
            }
        }
        return dp[s1.length()][s2.length()];
    }
}

上述空间复杂度为O(mn)，可以进行空间优化

 求解dp[i][j]时，会使用到 dp[i-1][j]和 dp[i][j-1]，即状态dp[i][j]只与dp[i-1][j] 和 dp[i][j-1]有关，如下图所示：

可以使用一维数组进行空间优化，对于 dp[i][j]的更新是从上往下，从左往右进行更新的，最终需要的结果右下角的值，所以可以使用一维数组 dp[i]进行保存每一行的结果：

1. 初始时dp[i]保存第一行每一列的结果
2. 求解第二行时，在更新前，dp[i]就是 dp[i][j-1]，dp[i-1]就是dp[i-1][j]，所以对于dp[i]的求解就变为：
   1. 当 i >0时，dp[ j ] = dp[j] && s1.charAt(i-1)==s3.charAt(i+j-1)
   2. 当 j > 0时，dp[ j ] |= dp[ j-1 ] && s2.charAt(j-1) == s3.charAt(i+j-1) 

AC代码

class Solution {
   public static boolean isInterleave(String s1, String s2, String s3) {
        if (s1.length() + s2.length() != s3.length()) {
            return false;
        }
        if (s1.length() == 0 || s2.length() == 0) {
            return s3.equals(s1) || s3.equals(s2);
        }
        boolean[]dp = new boolean[s2.length() + 1];
        dp[0]=true;
        for (int i = 0; i <= s1.length(); i++) {
            for (int j = 0; j <= s2.length(); j++) {
                if (i > 0) {
                    dp[j] = dp[j] && s1.charAt(i-1) == s3.charAt(i + j - 1);
                }
                if (j > 0) {
                    dp[j] |= dp[j - 1] && s2.charAt(j-1) == s3.charAt(i + j - 1);
                }
            }
        }
        return dp[s2.length()];
    }
}