考点之数据结构
概论
时间复杂度和空间复杂度是计算机科学中用来评估算法性能的重要指标。
时间复杂度:
时间复杂度衡量的是算法运行所需的时间。它表示算法执行所需的基本操作数量随着输入大小的增长而变化的趋势。
求法:
通常通过分析算法中基本操作执行的次数来计算时间复杂度。这可以通过以下步骤完成:
- 识别基本操作:找出算法中执行次数较多或者频繁的基本操作。
- 设置算法的输入规模:用一个变量(如n)表示输入的规模。
- 建立算法的执行次数表示:用算法中基本操作执行的次数来表示算法的执行时间,通常使用大 O 表示法(比如 O(n)、O(n^2) 等)。
- 计算最坏情况:通常分析最坏情况下的时间复杂度,因为它能提供对算法性能上限的评估。
空间复杂度:
空间复杂度是对算法在运行过程中所需的存储空间的度量,也就是算法所使用的内存量。
求法:
计算空间复杂度可以按以下步骤进行:
- 计算变量空间:识别算法中使用的变量、数据结构和存储空间,包括输入、输出以及临时空间的需求。
- 根据规模设置空间变量:和时间复杂度类似,使用变量(如n)来表示输入规模。
- 建立空间需求的表示:基于所用变量和数据结构的空间需求,表示算法的空间消耗,通常也使用大 O 表示法。
这些复杂度指标对于评估算法的效率和性能至关重要。优化算法以降低时间复杂度和空间复杂度是算法设计中的核心目标。
这里似乎有一些关于链表和顺序表的基本操作以及待完成的任务列表。首先,我会解释一些与链表和顺序表相关的操作:
顺序表(Array List):
顺序表是一种基于数组实现的线性表,它按照元素在内存中的相邻顺序进行存储。顺序表的特点是可以快速地通过下标直接访问元素,但在插入或删除元素时可能需要移动其他元素,导致效率低下。
链表(Linked List):
链表是一种基于节点的数据结构,它包含一个指向下一个节点的指针。主要有单链表和双链表两种形式。
单链表(Singly Linked List):
单链表中的每个节点包含一个指向下一个节点的指针,最后一个节点指向空值。删除单链表中相同值的节点通常需要遍历链表,判断节点值并删除。
双链表(Doubly Linked List):
双链表中的节点包含两个指针,分别指向前一个节点和后一个节点。循环双向链表是一种特殊的双链表,其尾节点指向头节点,形成一个闭环。
对于链表中的待完成任务:
- 逆置(Reverse):将链表中的节点顺序颠倒。
- 最值(Maximum/Minimum):在链表中查找最大或最小值的节点。
- 划分(Partition):按照特定条件(如某个值)划分链表。
- 归并(Merge):合并两个有序链表。
头插法(Head Insertion):
在链表中插入元素时,将新节点插入到链表的头部。
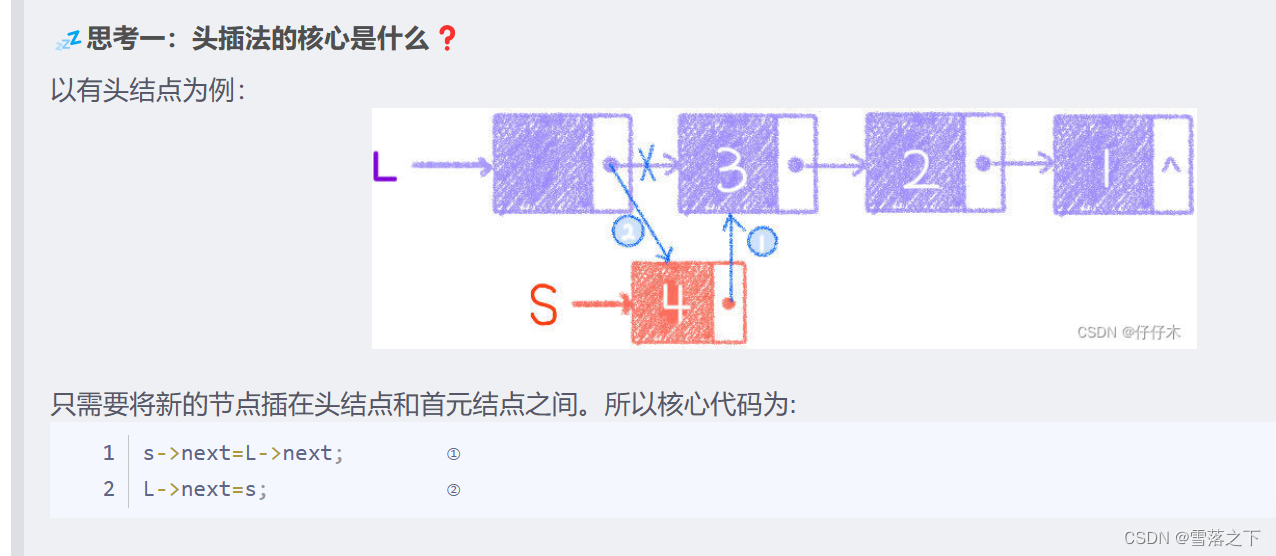

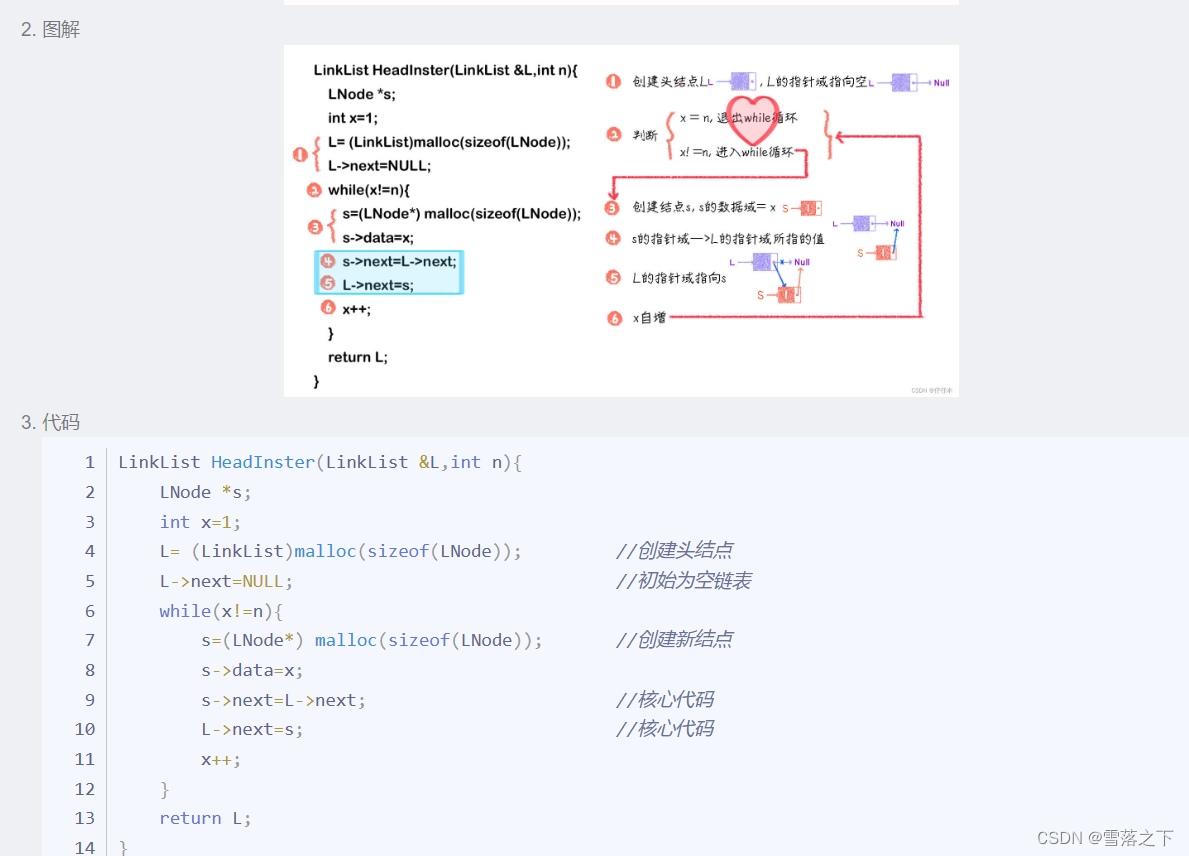


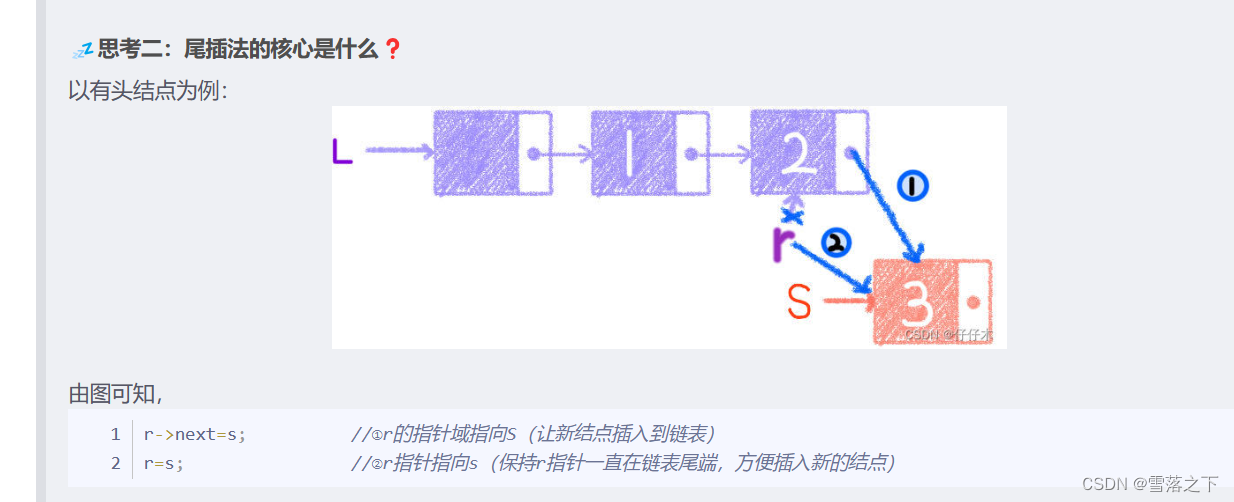
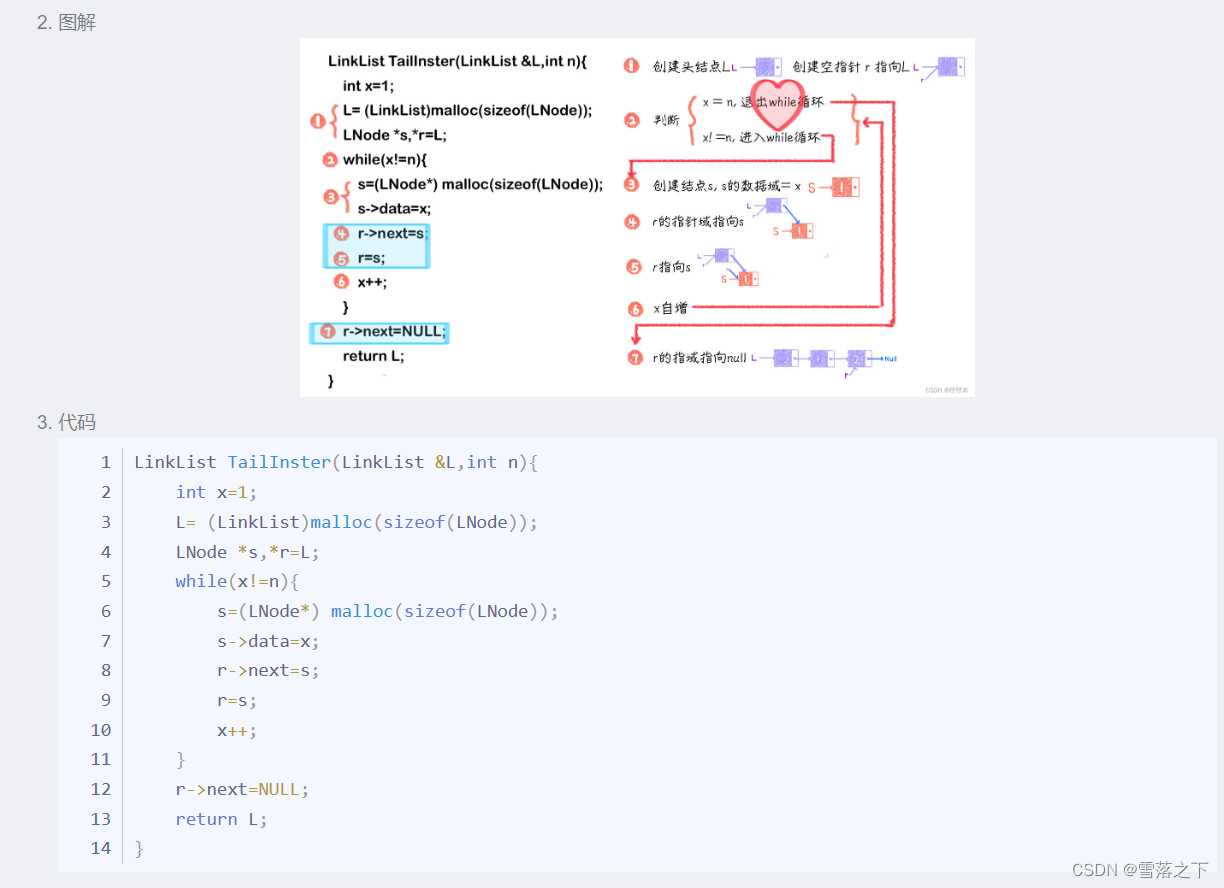
尾插法(Tail Insertion):
在链表中插入元素时,将新节点插入到链表的尾部。
以上提到的操作都是链表和顺序表中常见的操作,可以根据具体情况实现相应的算法和代码。对于链表的每个任务,需要编写相应的算法来实现所需的操作。

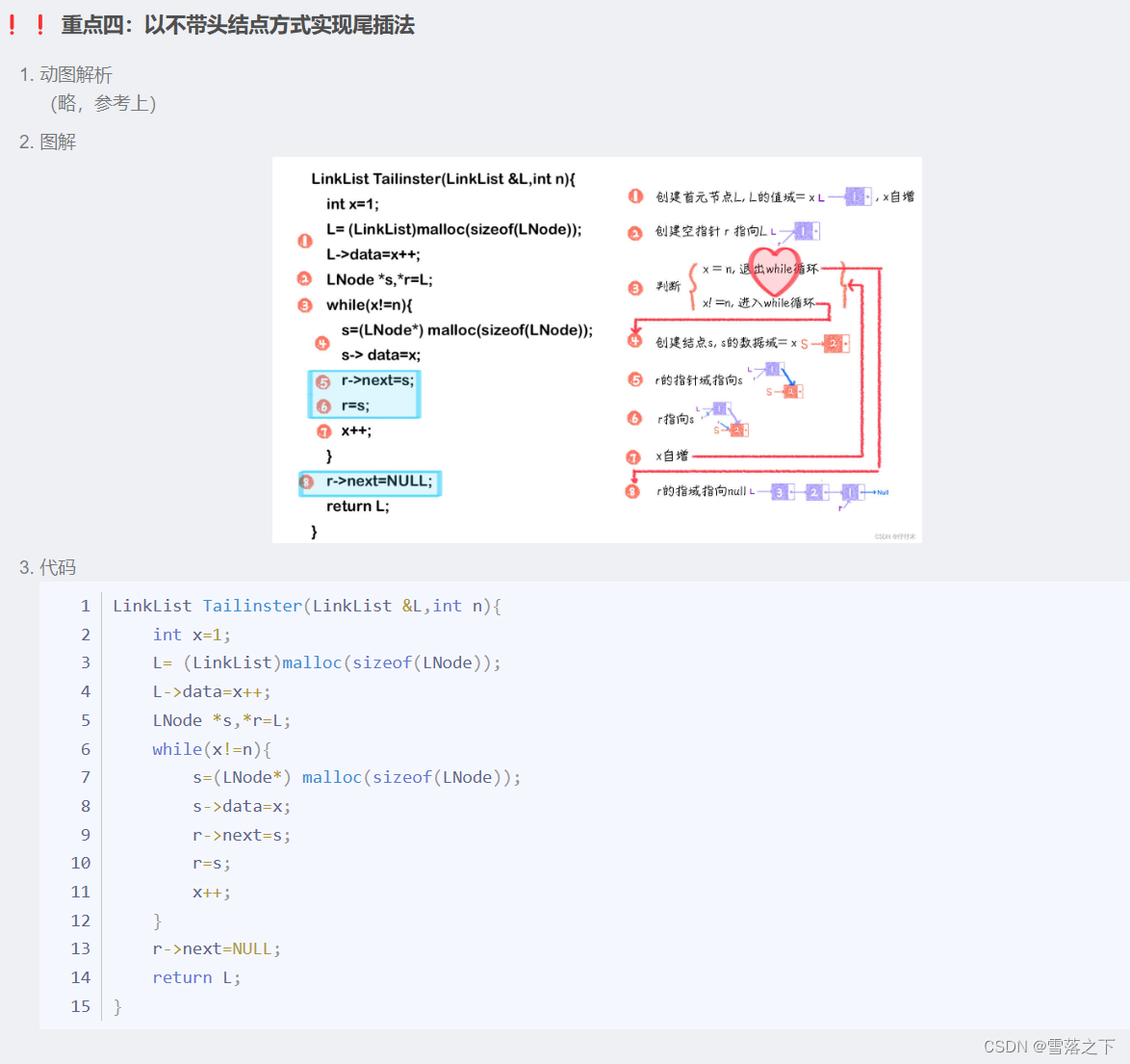
- 整体代码
#include "stdio.h"
#include "stdlib.h"
typedef int ElemType;
typedef struct LNode{
ElemType data; //数据域
struct LNode *next; //指针域
}LNode,*LinkList;
/*
* 头插法 有头结点
*/
LinkList HeadInster(LinkList &L,int n){
LNode *s;
int x=1;
L= (LinkList)malloc(sizeof(LNode)); //创建头结点
L->next=NULL; //初始为空链表
while(x!=n){
s=(LNode*) malloc(sizeof(LNode)); //创建新结点
s->data=x;
s->next=L->next;
L->next=s;
x++;
}
return L;
}
/*
* 头插法 无头结点
*/
LinkList Headinster(LinkList &L,int n){
LNode *s;
int x=1;
L= (LinkList)malloc(sizeof(LNode));
L->data=x++;
L->next=NULL;
while(x!=n){
s=(LNode*) malloc(sizeof(LNode));
s->data=x;
s->next=L;
L=s;
x++;
}
return L;
}
/*
* 尾插法、有结点
*/
LinkList TailInster(LinkList &L,int n){
int x=1;
L= (LinkList)malloc(sizeof(LNode));
LNode *s,*r=L;
while(x!=n){
s=(LNode*) malloc(sizeof(LNode));
s->data=x;
r->next=s;
r=s;
x++;
}
r->next=NULL;
return L;
}
/*
* 尾插法、无结点
*/
LinkList Tailinster(LinkList &L,int n){
int x=1;
L= (LinkList)malloc(sizeof(LNode));
L->data=x++;
LNode *s,*r=L;
while(x!=n){
s=(LNode*) malloc(sizeof(LNode));
s->data=x;
r->next=s;
r=s;
x++;
}
r->next=NULL;
return L;
}
/*
* 便利链表、头结点
*/
void PrintList(LinkList L){
LNode *s;
s=L->next;
while (s!=NULL) {
printf("%d\t",s->data);
s=s->next;
}
}
/*
* 便利链表
*/
void Print(LinkList L){
LNode *s;
s=L;
while (s!=NULL) {
printf("%d\t",s->data);
s=s->next;
}
}
int main(){
LinkList L,S,P,Q;
printf("有头结点的头插法:");
HeadInster(L,10);
PrintList(L);
printf("\n无头结点的头插法:");
Headinster(P,10);
Print(P);
printf("\n有头结点的尾插法:");
Tailinster(S,10);
Print(S);
printf("\n无头结点的尾插法:");
Tailinster(Q,10);
Print(Q);
}
栈
实现查找某一个位置的元素
顺序栈基本操作:
压栈(Push):将元素放入栈顶。即,在栈顶添加一个元素。
出栈(Pop):从栈顶移除元素。即,移除栈顶的元素并返回它。
插入(Insert):顺序栈通常只允许在栈顶进行插入操作,即压栈操作。
删除(Delete):顺序栈中删除操作一般指出栈操作,移除栈顶元素。
查找(Search):可以查找栈中特定元素的位置或者判断栈中是否存在某个元素。
这些操作的实现基于顺序栈的特性,可以使用数组来实现栈的这些功能。以下是伪代码表示顺序栈的基本操作:
数据结构顺序栈:
初始化栈(初始化数组大小、栈顶指针等)
push(元素):
如果栈已满:
返回栈已满
否则:
将元素放入栈顶
栈顶指针加一
pop():
如果栈为空:
返回栈为空
否则:
弹出栈顶元素
栈顶指针减一
insert(元素):
与push操作相同,向栈中压入元素
delete():
与pop操作相同,从栈中移除栈顶元素
search(元素):
从栈顶开始遍历栈中元素:
如果找到指定元素:
返回该元素在栈中的位置(或者True)
如果遍历结束未找到元素:
返回未找到该元素(或者False)
代码:
#include <stdio.h>
#include <stdbool.h>
#define MAX_SIZE 5
struct SequenceStack {
int stack[MAX_SIZE];
int top;
};
// 初始化栈
void initStack(struct SequenceStack *s) {
s->top = -1; // 初始化栈顶指针
}
// 判断栈是否为空
bool isEmpty(struct SequenceStack *s) {
return s->top == -1;
}
// 判断栈是否已满
bool isFull(struct SequenceStack *s) {
return s->top == MAX_SIZE - 1;
}
// 元素压栈
void push(struct SequenceStack *s, int element) {
if (isFull(s)) {
printf("Stack is full. Cannot push element.\n");
return;
}
s->top++;
s->stack[s->top] = element;
}
// 元素出栈
int pop(struct SequenceStack *s) {
if (isEmpty(s)) {
printf("Stack is empty. Cannot pop element.\n");
return -1;
}
int element = s->stack[s->top];
s->top--;
return element;
}
// 元素插入(与压栈操作相同)
void insert(struct SequenceStack *s, int element) {
push(s, element);
}
// 删除元素(与出栈操作相同)
int delete(struct SequenceStack *s) {
return pop(s);
}
// 查找元素在栈中的位置
int search(struct SequenceStack *s, int element) {
for (int i = s->top; i >= 0; i--) {
if (s->stack[i] == element) {
return i; // 返回元素在栈中的位置
}
}
return -1; // 元素未找到
}
int main() {
struct SequenceStack stack;
initStack(&stack); // 初始化栈
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
printf("Stack after pushing elements: ");
for (int i = 0; i <= stack.top; i++) {
printf("%d ", stack.stack[i]);
}
printf("\n");
printf("Popped element: %d\n", pop(&stack));
printf("Stack after popping element: ");
for (int i = 0; i <= stack.top; i++) {
printf("%d ", stack.stack[i]);
}
printf("\n");
int position = search(&stack, 20);
if (position != -1) {
printf("Element 20 found at position %d in the stack.\n", position);
} else {
printf("Element 20 not found in the stack.\n");
}
return 0;
}
链栈
- 链栈基本操作:
压栈(Push):将元素放入栈顶。在链栈中,通常指的是在链表的头部添加一个新节点。
出栈(Pop):从栈顶移除元素。在链栈中,即删除链表的头节点,并返回其值。
栈内容转置:将链栈中的内容顺序颠倒,可以利用辅助栈或指针进行转置操作。
入栈顺序、出栈顺序:通过尝试不同的出栈顺序来计算入栈顺序有几种、判断是否合法。
以下是链栈的相关操作实现以及入栈、出栈顺序检验的基本思路:
链栈基本操作的 C 语言实现:
#include <stdio.h>
#include <stdlib.h>
// 链表节点定义
struct Node {
int data;
struct Node* next;
};
// 链栈定义
struct LinkedStack {
struct Node* top;
};
// 初始化栈
void initStack(struct LinkedStack* stack) {
stack->top = NULL; // 栈顶初始化为空
}
// 判断栈是否为空
int isEmpty(struct LinkedStack* stack) {
return (stack->top == NULL); // 若栈顶为空则栈为空
}
// 压栈操作
void push(struct LinkedStack* stack, int value) {
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node)); // 创建新节点
newNode->data = value;
newNode->next = stack->top; // 新节点作为栈顶
stack->top = newNode;
}
// 出栈操作
int pop(struct LinkedStack* stack) {
if (isEmpty(stack)) {
printf("Stack is empty. Cannot pop element.\n");
return -1;
}
int value = stack->top->data;
struct Node* temp = stack->top;
stack->top = stack->top->next; // 栈顶指针移至下一个节点
free(temp); // 释放原栈顶节点
return value;
}
// 栈内容转置
void reverseStack(struct LinkedStack* stack) {
struct LinkedStack tempStack;
initStack(&tempStack); // 初始化临时栈
while (!isEmpty(stack)) {
int value = pop(stack); // 从原栈弹出元素
push(&tempStack, value); // 推入临时栈
}
stack->top = tempStack.top; // 将临时栈内容赋给原栈
}
int main() {
struct LinkedStack stack;
initStack(&stack); // 初始化栈
// 入栈
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
// 显示转置前的栈内容
printf("Stack content before reversal: ");
while (!isEmpty(&stack)) {
printf("%d ", pop(&stack));
}
printf("\n");
// 重新入栈
push(&stack, 10);
push(&stack, 20);
push(&stack, 30);
// 栈内容转置
reverseStack(&stack);
// 显示转置后的栈内容
printf("Stack content after reversal: ");
while (!isEmpty(&stack)) {
printf("%d ", pop(&stack));
}
printf("\n");
return 0;
}
队列
循环队列是一种基于数组实现的队列,通过循环利用数组空间来实现队列的基本操作。求解循环队列中元素个数的方法很简单,可以通过队头和队尾指针的位置关系来进行计算。
循环队列的基本操作:
- 初始化:设置队列的大小,队头、队尾指针等。
- 入队:将元素添加到队列尾部。
- 出队:从队列头部移除元素。
- 判空:判断队列是否为空。
- 判满:判断队列是否已满。
- 求元素个数:计算队列中当前元素的个数。
以下是一个 C 语言实现的循环队列示例代码,并计算队列中元素的个数:
#include <stdio.h>
#include <stdbool.h>
#define MAX_SIZE 5
struct CircularQueue {
int items[MAX_SIZE];
int front, rear;
int count; // 用来统计元素个数
};
// 初始化队列
void initQueue(struct CircularQueue* queue) {
queue->front = 0;
queue->rear = -1;
queue->count = 0;
}
// 判空
bool isEmpty(struct CircularQueue* queue) {
return (queue->count == 0);
}
// 判满
bool isFull(struct CircularQueue* queue) {
return (queue->count == MAX_SIZE);
}
// 入队
void enqueue(struct CircularQueue* queue, int value) {
if (!isFull(queue)) {
queue->rear = (queue->rear + 1) % MAX_SIZE;
queue->items[queue->rear] = value;
queue->count++;
} else {
printf("Queue is full. Cannot enqueue element.\n");
}
}
// 出队
int dequeue(struct CircularQueue* queue) {
if (!isEmpty(queue)) {
int dequeuedItem = queue->items[queue->front];
queue->front = (queue->front + 1) % MAX_SIZE;
queue->count--;
return dequeuedItem;
} else {
printf("Queue is empty. Cannot dequeue element.\n");
return -1;
}
}
// 计算队列中元素个数
int countElements(struct CircularQueue* queue) {
return queue->count;
}
int main() {
struct CircularQueue queue;
initQueue(&queue);
enqueue(&queue, 10);
enqueue(&queue, 20);
enqueue(&queue, 30);
enqueue(&queue, 40);
enqueue(&queue, 50);
printf("Number of elements in the queue: %d\n", countElements(&queue));
return 0;
}
这段代码实现了一个循环队列,并通过 countElements() 函数计算了队列中元素的个数。在 main() 函数中,演示了向队列中添加元素后如何计算队列中的元素个数。
串(顺序存储)
顺序存储的串是一种由字符数组构成的字符串,其中每个字符按照特定顺序依次排列。在顺序存储的串中,可以进行插入、删除、查找等操作,并且可以实现串的比较、统计每个元素出现的次数以及区分空串和空格串。
插入、删除、查找
- 插入:在串的任意位置插入一个字符或者另一个串。
- 删除:删除串中指定位置的字符或一段字符。
- 查找:查找串中特定的子串或字符。
串的比较
串的比较是指比较两个串的大小关系,可以根据字典序等规则来进行比较。
每个元素出现次数
统计每个元素在串中出现的次数,遍历串并计数即可实现。
空串和空格串的区别
- 空串:指的是一个没有任何字符的串,长度为0。
- 空格串:指的是串中只包含空格字符(ASCII码为32)的串,长度大于等于1。
下面是一个 C 语言示例,展示了如何进行这些操作:
#include <stdio.h>
#include <string.h>
// 插入字符
void insertChar(char str[], char ch, int position) {
memmove(&str[position + 1], &str[position], strlen(str) - position + 1);
str[position] = ch;
}
// 删除字符
void deleteChar(char str[], int position) {
memmove(&str[position], &str[position + 1], strlen(str) - position);
}
// 查找字符
int findChar(char str[], char ch) {
char *ptr = strchr(str, ch);
if (ptr != NULL) {
return ptr - str; // 返回找到的位置
} else {
return -1; // 没找到返回-1
}
}
// 串的比较
int compareStrings(char str1[], char str2[]) {
return strcmp(str1, str2);
}
// 统计每个元素出现次数
void countOccurrences(char str[]) {
int count[256] = {0}; // 256个ASCII字符,初始化计数为0
for (int i = 0; str[i] != '\0'; i++) {
count[(int)str[i]]++; // 统计字符出现次数
}
for (int i = 0; i < 256; i++) {
if (count[i] > 0) {
printf("Character '%c' occurs %d times.\n", i, count[i]);
}
}
}
int main() {
char str[] = "Hello World";
insertChar(str, 'X', 3); // 在位置3插入字符X
printf("After insertion: %s\n", str);
deleteChar(str, 7); // 删除位置7的字符
printf("After deletion: %s\n", str);
int position = findChar(str, 'W'); // 查找字符W的位置
if (position != -1) {
printf("Character found at position %d\n", position);
} else {
printf("Character not found\n");
}
char str1[] = "Hello";
char str2[] = "World";
int comparison = compareStrings(str1, str2);
if (comparison == 0) {
printf("The strings are equal\n");
} else if (comparison < 0) {
printf("String 1 is less than string 2\n");
} else {
printf("String 1 is greater than string 2\n");
}
countOccurrences(str); // 统计字符出现次数
return 0;
}
这个示例程序包含了插入、删除、查找字符,串的比较,以及统计每个元素出现次数的操作。你可以根据需要进行调整和扩展。
数组
二维数组的地址运算
在 C 语言中,二维数组在内存中是按行存储的。数组名代表数组的起始地址,而对于二维数组,可以通过下标访问元素。地址运算可以使用指针来完成,计算特定元素的地址。
假设有一个二维数组 arr[row][col]:
- 访问元素
arr[i][j]的地址:&arr[i][j]或(arr + i * col + j)。
对称矩阵的地址运算
对称矩阵是一个方阵,其下三角或上三角对角线对称。这意味着实际上只需要存储其中一半的元素。当以一维数组表示时,元素的排列方式决定了地址的计算。
如果将对称矩阵存储在一维数组中:
- 访问元素
arr[i][j]的地址:将二维坐标(i, j)映射到一维数组的地址。
稀疏矩阵的表示方法
稀疏矩阵是大部分元素为0的矩阵。稀疏矩阵常用三元组表或十字链表来表示。
- 三元组表:记录非零元素的行、列以及元素值。
- 十字链表:将非零元素的行、列和值存储在节点中,并使用链表连接。
对于三元组表的转置,只需要交换行和列的位置即可。
三对角阵
三对角矩阵是一种特殊的矩阵,除主对角线外,只有相邻对角线和主对角线上的元素可能非零。在一维数组中存储时,通常以紧凑形式存储,即仅存储主对角线和两个相邻对角线上的元素。
- 访问元素
arr[i][j]的地址:将二维坐标(i, j)映射到一维数组的地址。
特殊矩阵在一维数组中存储
特殊矩阵(如对称矩阵、三对角矩阵等)在一维数组中存储时,可以利用数学性质和矩阵的结构,减少存储空间并优化访问速度。
以下是一个 C 语言的示例,展示了对称矩阵和三对角矩阵在一维数组中存储的方式:
#include <stdio.h>
// 访问对称矩阵元素的地址
int getAddressSymmetric(int row, int col, int n) {
if (row >= col) {
return (row * (row + 1) / 2) + col;
} else {
return (col * (col + 1) / 2) + row;
}
}
// 访问三对角矩阵元素的地址
int getAddressTridiagonal(int row, int col, int n) {
int diff = row - col;
if (diff == 0) {
return row;
} else if (diff == 1) {
return n + row - 1;
} else if (diff == -1) {
return 2 * n + row - 1;
} else {
return -1; // 非三对角元素,根据需求自行扩展
}
}
int main() {
int n = 5; // 矩阵大小
int symmetric[n * (n + 1) / 2];
int tridiagonal[3 * n - 2];
int row = 2, col = 3;
int addressSymmetric = getAddressSymmetric(row, col, n);
int addressTridiagonal = getAddressTridiagonal(row, col, n);
printf("Address in symmetric matrix: %d\n", addressSymmetric);
printf("Address in tridiagonal matrix: %d\n", addressTridiagonal);
return 0;
}
这个示例程序展示了如何计算对称矩阵和三对角矩阵在一维数组中的地址。你可以根据需求扩展这些函数以适应不同类型的特殊矩阵。
二叉树
1. 性质
- 二叉树是由节点组成的树状结构,每个节点最多有两个子节点,分别为左子节点和右子节点。
- 左子节点小于或等于父节点,右子节点大于父节点的二叉树称为二叉搜索树。
- 遍历二叉树有三种基本顺序:前序(根-左-右)、中序(左-根-右)、后序(左-右-根)。
- 完全二叉树是一个除了最底层外所有层都是满的,并且最底层的节点尽可能地集中在树的左边的二叉树。
2. 遍历
- 前序遍历:根-左-右
- 中序遍历:左-根-右
- 后序遍历:左-右-根
- 层次遍历:逐层从左到右遍历
3. 线索二叉树
- 线索二叉树是为了加速遍历而提出的,它的每个节点指向其前驱和后继节点。通过线索化,可以不使用递归或栈来进行遍历。
4. 二叉排序树
- 二叉排序树(BST)是一种特殊的二叉树,其中每个节点的左子树都小于节点的值,右子树都大于节点的值。
- 插入:按照大小顺序找到合适的位置插入新节点。
- 删除:根据情况考虑删除节点:若无子节点直接删除,若有一个子节点则用其子节点替代,若有两个子节点则选择左子树最大节点或右子树最小节点替代删除节点。
5. 完全二叉树
- 完全二叉树是一种特殊的二叉树,除了最底层,其他层都是满的,并且最底层的节点尽可能地集中在树的左边。
- 层次遍历是一个实现完全二叉树的有效方法。
6. 满二叉树
- 满二叉树是一种特殊的二叉树,每一层的节点数都达到最大值。
7. 哈夫曼树
- 哈夫曼树是一种带权路径长度最短的二叉树。通过构建哈夫曼树,可以实现数据的最优编码。
画出哈夫曼树
Example:
30
/ \
10 20
/ \ / \
5 3 7 7
编程实现
哈夫曼树的实现通常需要建立优先队列,并进行树的合并和构建。以下是一个简单的示例:
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node *left, *right;
};
struct Node* createNode(int data) {
struct Node* node = (struct Node*)malloc(sizeof(struct Node));
node->data = data;
node->left = node->right = NULL;
return node;
}
int main() {
struct Node *root = createNode(30);
root->left = createNode(10);
root->right = createNode(20);
root->left->left = createNode(5);
root->left->right = createNode(3);
root->right->left = createNode(7);
root->right->right = createNode(7);
return 0;
}
这段代码创建了一个简单的哈夫曼树结构。实际的哈夫曼编码需要根据数据频率动态构建树,并实现编码和解码操作。
图
图相关算法和表示方法
1. 遍历(DFS、BFS)
- 深度优先搜索 (DFS):沿着图的深度遍历,尽可能深地搜索图的分支。
- 广度优先搜索 (BFS):逐层访问邻居节点,先访问离起始节点最近的节点。
2. 最小生成树(prim、kruskal)
- Prim 算法:从一个顶点开始,每次选择一条权值最小的边来连接到新的顶点,直到覆盖所有的顶点。
- Kruskal 算法:按边的权值从小到大顺序选择边,若加入该边不产生回路,则加入,直到覆盖所有的顶点。
3. 最短路径(Dijkstra、Floyd)
- Dijkstra 算法:基于贪心策略,逐步扩展路径,找出起点到其他顶点的最短路径。
- Floyd 算法:通过动态规划,逐步更新最短路径,计算图中任意两点之间的最短路径。
4. 关键路径
- 关键路径:在一个有向图中,表示从起始节点到结束节点的最长路径,决定了整个图的时间长度。
5. 拓扑排序
- 拓扑排序:针对有向无环图,通过对顶点排序使得图中的每条有向边从低序顶点指向高序顶点。
6. 邻接表/邻接矩阵表示图
- 邻接表:使用链表存储图的顶点和相邻顶点的关系。
- 邻接矩阵:使用二维数组存储图的顶点和边的关系。
7. 深度优先遍历序列
- 深度优先遍历序列:记录顶点被访问的先后顺序。
8. 稀疏矩阵的十字链表表示法
- 十字链表:一种表示稀疏矩阵的方法,结合链表结构实现矩阵的压缩存储。使用两类链表,分别表示非零元素和维度信息。
以下是一个 C 语言示例,展示了稀疏矩阵的十字链表表示法:
检索
线性表检索是在线性结构数据中进行搜索特定元素的过程。常见的线性表检索方法包括顺序查找、二分查找和分块查找。
1. 顺序查找(Sequential Search)
- 顺序查找是最简单直接的查找方法。它从线性表的第一个元素开始逐个扫描,直到找到目标元素或者遍历整个表。
顺序查找的步骤:
- 从表的第一个元素开始,逐个和目标元素进行比较。
- 如果找到目标元素,返回元素的位置;否则,返回未找到的标识。
2. 二分查找(Binary Search)
- 二分查找是在有序数组中进行查找的有效方法。它通过将目标值和有序数组的中间值进行比较,并据此决定将搜索范围缩小为前半部分或后半部分。
二分查找的步骤:
- 确保数组是有序的。
- 确定搜索范围的左右边界。
- 计算中间元素的索引。
- 将目标值与中间值比较。
- 如果目标值大于中间值,缩小搜索范围至右半部分;否则,缩小至左半部分。
- 重复这个过程直至找到目标值或搜索范围缩小为 0。
3. 分块查找(Block Search)
- 分块查找是对元素进行分块,然后在块内进行顺序查找,同时查找块的索引,最终确定元素的位置。
分块查找的步骤:
- 将线性表分成若干块,每个块内的元素可以是无序的。
- 建立一个块的索引表,记录每块的起始位置和最大值。
- 通过查找块索引表找到目标元素应该在的块。
- 在该块内进行顺序查找。
这些检索方法在不同情况下有着不同的适用性。例如,顺序查找适用于未排序或少量元素的线性表,而二分查找适用于已排序的线性表。分块查找结合了两者的优点,在大规模数据的情况下可以减少搜索的时间复杂度。
你可以根据数据的特性和检索的要求选择合适的检索算法。
散列表
散列表(Hash Table)是一种数据结构,旨在实现快速的数据检索。它通过哈希函数将关键字映射到哈希表中的位置。不同的冲突解决方法,例如线性探测、二次探测以及拉链法,用于处理不同的哈希冲突。
如何建立一个表
1. 哈希函数
- 哈希函数将关键字映射到哈希表中的位置。
- 关键是设计一个均匀、不易产生冲突的哈希函数。
2. 不同的冲突解决方法
a. 线性探测
- 线性探测是一种解决冲突的方法。如果哈希函数产生了冲突,它会在哈希表中的下一个位置继续寻找空槽。
- 冲突解决公式为 ( h(k, i) = (h’(k) + i) \mod m ),其中 (h’(k)) 是哈希函数,(i) 是探测序列,(m) 是表的大小。
b. 二次探测
- 二次探测是线性探测的改进,它采用二次方程进行步长探测,以避免线性探测可能出现的线性探测失效的问题。
- 冲突解决公式为 ( h(k, i) = (h’(k) + c_1 \cdot i + c_2 \cdot i^2) \mod m ),其中 (c_1, c_2) 是常数。
c. 拉链法(Chaining)
- 拉链法使用链表解决冲突。当哈希函数产生冲突时,将具有相同哈希值的元素存储在同一位置的链表中。
开放地址法和链地址法求平均查找长度(Average Search Length, ASL)
开放地址法
- ASL 是在散列表中查找元素时所需的平均操作数。
- 对于开放地址法,ASL 取决于装填因子(load factor)和冲突解决方法。
链地址法
- 链地址法中的 ASL 通常取决于装填因子和链表长度的平均值。
ASL 的公式可以根据不同的冲突解决方法和装填因子来计算。例如,对于线性探测和二次探测,ASL 的计算与冲突的发生和解决次数相关。对于拉链法,ASL 取决于链表长度的平均值。
这些方法的选择取决于实际应用需求和数据特征。例如,对于大型数据集,装填因子要小,而对于小型数据集,可以选择拉链法等方法。
内排序
内排序算法
内排序是对存储在内存中的数据进行排序的过程。它涉及的数据量通常不超过计算机的内存容量。
1. 冒泡排序(Bubble Sort)
- 冒泡排序是一种简单的排序算法,它重复地走访要排序的数列,依次比较相邻的两个元素,将较大的元素交换到右侧。
- 时间复杂度:平均情况和最坏情况都为 O(n^2)。
2. 快速排序(Quick Sort)
- 快速排序采用分治策略,选择一个基准值,将小于基准值的元素放在左侧,大于基准值的元素放在右侧。然后递归地对左右两部分进行排序。
- 时间复杂度:平均情况下为 O(n log n),最坏情况下为 O(n^2)。
3. 基数排序(Radix Sort)
- 基数排序是一种非比较型的排序算法,它按照低位先排序,然后收集,再按照高位排序,再收集,以此类推,直到高位。
- 时间复杂度:O(k * n),其中 k 为数字位数。
4. 堆排序(Heap Sort)
- 堆排序利用堆的性质进行排序。它将待排序的序列构建成一个大顶堆(或小顶堆),依次取堆顶元素,然后重新调整堆,直到排序完成。
- 时间复杂度:平均、最坏和最好情况下都为 O(n log n)。
5. Shell排序(Shell Sort)
- Shell排序是一种插入排序的变体,它通过比较相距一定间隔的元素来工作,使离正确位置很远的元素能快速回到合适位置。
- 时间复杂度:取决于选取的增量序列,平均情况下为 O(n log n)。
这些算法在不同场景下有着不同的效率表现,适合处理不同规模和类型的数据。冒泡和快速排序都属于交换排序,而基数排序、堆排序和Shell排序则是其他类型的排序算法。
你可以根据数据的规模和特征,选择最适合的排序算法来进行排序。
数据结构和数据类型
数据结构和数据类型是计算机科学中两个相关但不同的概念。
数据结构是一种组织和存储数据的方式,它定义了数据元素之间的关系以及对这些数据元素进行操作的规则。数据结构可以是线性的,如数组、链表等,也可以是非线性的,如树、图等。它们用于存储和处理数据,以便在计算机程序中执行各种操作,例如查找、排序、插入、删除等。
数据类型则是一种编程语言的特性,它定义了数据的性质和数据可以执行的操作。数据类型规定了数据的存储方式、范围和可执行的操作。常见的数据类型包括整数、浮点数、字符、布尔值等。编程语言使用数据类型来确保数据的正确性和一致性,以便在程序中进行类型检查和运算。
总结:
数据结构是用于组织和存储数据的方式,它涉及数据元素之间的关系和操作规则。
数据类型是编程语言中的概念,它规定了数据的性质和操作规则。
数据结构通常依赖于数据类型来存储和操作数据。
数据类型是编程语言的一部分,而数据结构是程序设计的一部分。
