密度聚类算法（DBSCAN）实验案例

描述

DBSCAN是一种强大的基于密度的聚类算法，从直观效果上看，DBSCAN算法可以找到样本点的全部密集区域，并把这些密集区域当做一个一个的聚类簇。DBSCAN的一个巨大优势是可以对任意形状的数据集进行聚类。

本任务的主要内容：

1、 环形数据集聚类

2、 新月形数据集聚类

3、 轮廓系数评估指标应用

源码下载

环境

• 操作系统：Windows 10、Ubuntu18.04

• 工具软件：Anaconda3 2019、Python3.7

• 硬件环境：无特殊要求

• 依赖库列表

  matplotlib   	3.3.4
  numpy 			1.19.5
  scikit-learn	0.24.2
  

分析

本实验包含三个任务：环形数据集聚类、新月数据集聚类以及轮廓系数评估指标的使用，数据集均由sklearn.datasets模块生成。为了直观观察DBSCAN的优势，任务中还引入了前面学过的多种聚类算法进行对比。

本实验涉及以下几个环节：

1）子任务一、环形数据聚类

1.1 数据集的生成

1.2 使用K-Means、MeanShift、Birch算法进行聚类并可视化

1.3 使用DBSCAN聚类并可视化

2）子任务二、新月数据集聚类

2.1 数据集的生成

2.2 使用K-Means、MeanShift、Birch算法进行聚类并可视化

2.3 使用DBSCAN聚类并可视化

3）聚类评估指标（轮廓系数）案例实践

3.1 数据集生成

3.2 聚类并评估效果

实施

1、环形数据集聚类

任务描述：

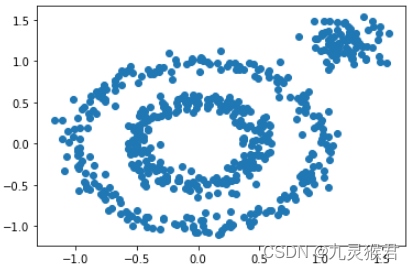
1、使用scikit-learn生成环形数据集；

2、将数据集聚成右侧3个类别。

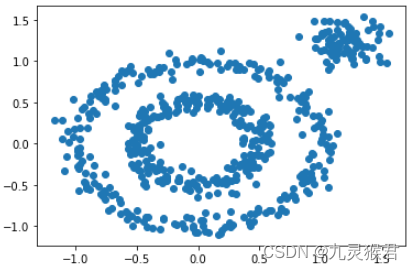
1.1 生成环形数据集

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

# 生成环形数据集（500个样本）
X1, y1=datasets.make_circles(n_samples=500, factor=0.5, noise=0.07, random_state=0)

# 生成点块数据集（80个样本）
X2, y2 = datasets.make_blobs(n_samples=80, n_features=2, centers=[[1.2, 1.2]], cluster_std=[[0.15]], random_state=0)

# 合并成一个数据集，生成散点图
X = np.concatenate((X1, X2))
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()

显示结果：

1.2 分别使用K-Means、MeanShift、Birch算法进行聚类

from sklearn.cluster import KMeans, MeanShift, Birch

# 尝试三种聚类模型，都不能达到目的
y_pred = KMeans(3).fit_predict(X) # KMeans

# y_pred = Birch(n_clusters=3).fit_predict(X) # Birch
# y_pred = MeanShift().fit_predict(X) # MeanShift
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

显示结果：

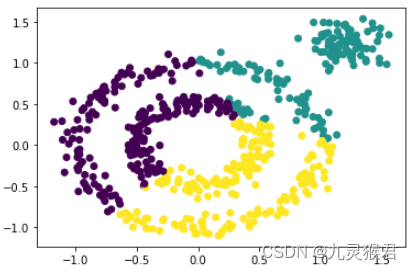
从算法的输出中可以看到，对于环形数据集，上述三种聚类算法均不能很好地实现任务规定的聚类目标。

1.3 使用DBSCAN算法（不指定参数）

from sklearn.cluster import DBSCAN

# 使用无参数的DBSCAN聚类，发现模型将所有样本归为了一类
y_pred = DBSCAN().fit_predict(X)

# 画散点图
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

显示结果：

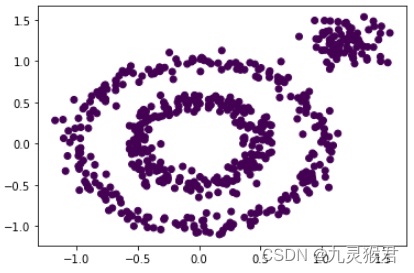
可以看到，不使用参数的DBSCAN算法，将所有数据分成了一类。

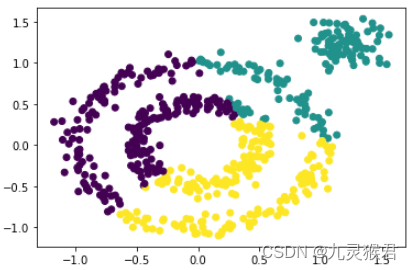
1.4 指定DBSCAN算法的参数

DBSCAN算法聚类的结果依赖于调参，该算法的两个主要参数eps和min_samples，对于聚类结果的影响很大。

# eps-临近半径
# min_samples-最小样本数
# 指定参数，调参，任务完成（聚成内、中、外3类）
y_pred = DBSCAN(eps=0.2, min_samples=2).fit_predict(X)

# 画散点图
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

输出结果：

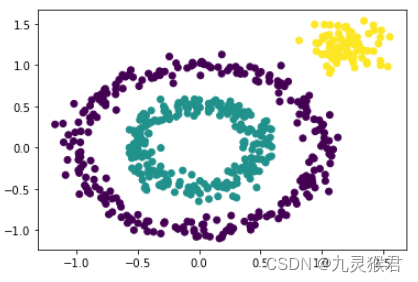
可以看到，通过调参，DBSCAN算法完美地将数据集按指定要求聚成了3类。

2、新月数据集聚类

任务描述：

1、使用scikit-learn生成新月数据集；

2、将数据集聚成右侧上下2个类别。

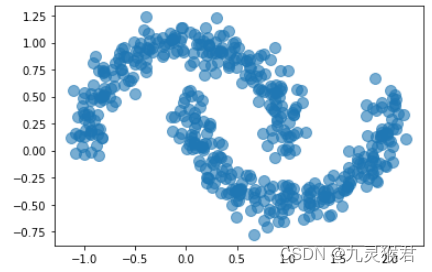
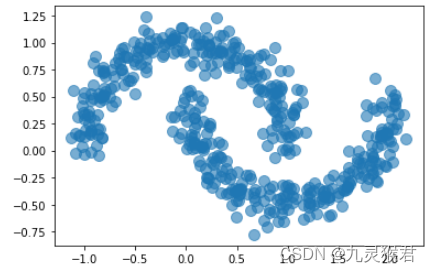
2.1 生成数据集

import matplotlib.pyplot as plt
from sklearn import datasets

# 生成弯月数据集（500个样本）
X, y = datasets.make_moons(500, noise = 0.1, random_state=99)

# 显示散点图
plt.scatter(X[:, 0], X[:, 1], s = 100, alpha = 0.6, cmap = 'rainbow')

plt.show()

显示结果：

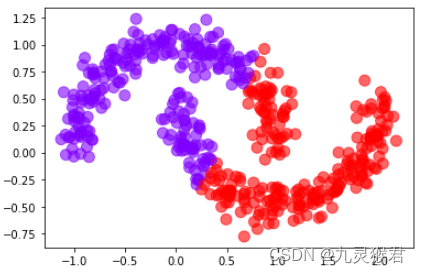
2.2 尝试K-Means、MeanShift、Birch算法

from sklearn.cluster import KMeans, MeanShift, Birch

# 尝试三种聚类模型，都不能达到目的
y_pred = KMeans(2).fit_predict(X) # KMeans

# y_pred = Birch(n_clusters=2).fit_predict(X) # Birch
# y_pred = MeanShift().fit_predict(X) # MeanShift
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s = 100, alpha = 0.6, cmap = 'rainbow')

plt.show()

显示结果：（对于该数据集，上述三种聚类算法不能很好地实现指定聚类目标。）

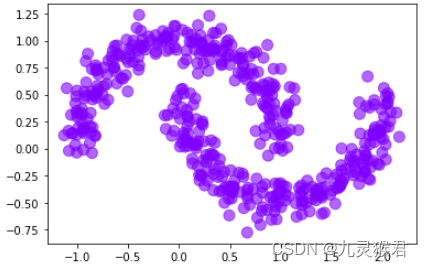
2.3 使用DBSCAN聚类算法，不指定参数

from sklearn.cluster import DBSCAN

# 使用DBSCAN算法（不指定参数）
y_pred = DBSCAN().fit_predict(X)

# 画散点图
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s = 100, alpha = 0.6, cmap = 'rainbow')

plt.show()

显示结果：

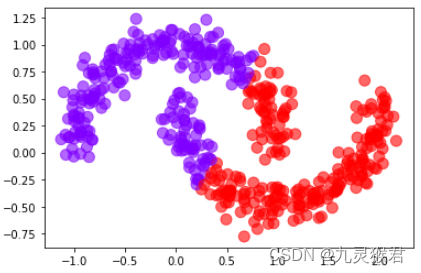
2.4 使用DBSCAN聚类算法，指定参数

# 指定参数，调参，任务完成（聚成上下2类）
y_pred = DBSCAN(eps=0.2, min_samples=9).fit_predict(X)

# 画散点图
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s = 100, alpha = 0.6, cmap = 'rainbow')

plt.show()

显示结果：

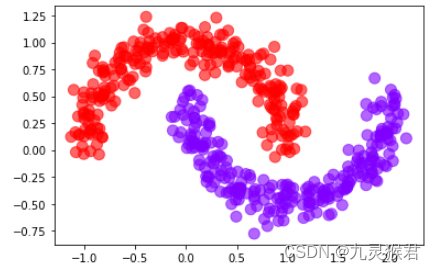
通过调整两个指定参数，DBSCAN算法按照要求完成了新月数据集的聚类，DBSCAN算法的一大优势是可以对任意形状的数据集进行聚类。

3、使用轮廓系数（silhouette_score）来评估聚类

任务描述：

轮廓系数（silhouette_score）指标是聚类效果的评价方式之一（前面我们还使用了兰德指数-adjusted_rand_score，注意它们之间的区别）。轮廓系数指标不关注样本的实际类别，而是通过分析聚类结果中样本的内聚度和分离度两种因素来给出成绩，取值范围为（-1，1），值越大代表聚类的结果越合理。

3.1 生成数据集

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

# 使用数据生成器随机生成500个样本，每个样本2个特征
X, y = make_blobs(n_samples=500, n_features=2, centers=[[-1,-1], [0.5,-1]], cluster_std=[0.2, 0.3], random_state=6)

# 画出散点图
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()

显示结果：

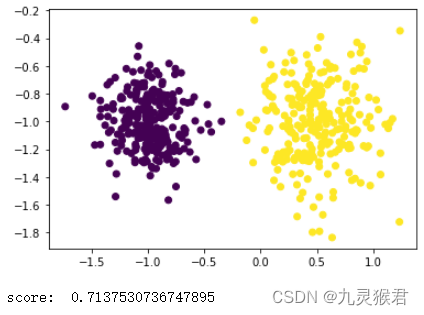
3.2 使用轮廓系数来评估聚类结果

from sklearn.metrics import silhouette_score # 轮廓系数评估函数
from sklearn.cluster import MeanShift

# 使用MeanShift聚类
y_pred = MeanShift().fit_predict(X)

# 画出聚类散点图
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show() 

# 评估轮廓系数
score = silhouette_score(X, y_pred)
print('score: ', score)