融合语言模型中的拓扑上下文和逻辑规则实现知识图谱补全11.18

摘要

知识图补全（KGC）旨在根据观察到的事实推断缺失的事实，这对许多下游应用程序具有重要意义。鉴于深度学习和预训练语言模型（LM）的成功，一些基于LM的方法被提出用于KGC任务。然而，它们中的大多数专注于对事实三元组的文本进行建模，而忽略了更深层次的语义信息（例如，拓扑上下文和逻辑规则），这对KG建模很重要。为此，我们提出了一个统一的框架FTL-LM来描述KGC语言模型中的拓扑上下文和逻辑规则，主要包括一种新的基于路径的拓扑上下文学习方法和一种变分期望最大化（EM）软逻辑规则提取算法。前者利用异构随机行走生成拓扑路径和进一步的推理路径，可以隐式地表示拓扑上下文，并可以显式地由LM建模。引入掩码语言建模和对比路径学习策略对这些拓扑上下文进行建模。后者隐式融合逻辑规则的变分EM算法与两个LM。具体地，在E步骤中，三元组LM在由固定规则LM验证的观察三元组和有效隐藏三元组的监督下被更新。在M步骤中，我们修复了三重LM并微调了规则LM以更新逻辑规则。在三个常见的KGC数据集上的实验证明了所提出的FTL-LM的优越性，例如，在WN 18 RR和FB 15 k-237中，与最先进的基于LM的模型LP-BERT相比，它分别实现了2.1%和3.1%的Hits@10改进。

1 引言

知识图谱（KGs）已经引起了人工智能（AI）社区的广泛关注，因为它们存储了大量的现实世界的事实知识。每个事实通常表示为三元组（h，r，t），其中h、r和t分别表示头实体、关系和尾实体，例如，(姚明，married to，叶莉）。有了高质量的KG，许多AI应用程序可以实现出色的准确性和可解释的推理过程，例如问答，语言建模，语义推理，推荐系统，情感分析和医疗智能。然而，由于有限的注释资源和技术，大多数KG的知识是不完整的，而不完整的KG无法满足下游应用的信息需求。因此，提出了知识图补全（KGC）任务，根据KG中观察到的隐藏三元组来推断新的有效隐藏三元组。一些KG嵌入方法，如TransE 和DistMult ，被提出来将实体和关系嵌入到连续向量空间中。然后，他们计算三元组的分数来完成推理。同时，为了对KG的拓扑进行建模，提出了一些图卷积网络（GCN）来融合实体的邻居信息，例如R-GCN 和CompGCN 。尽管这两种方法取得了巨大的成功，但它们只利用单个三元组或邻居信息，而它们的算法忽略了实体和关系的内在语义。例如，这些方法都没有考虑图1中的实体姚明的实际语义，即，他是一个出生在中国的NBA球员，这导致信息建模和推理性能不足。鉴于此，提出了一些基于语言模型（LM）的KGC方法，其中KG-BERT和StAR是代表性的研究。

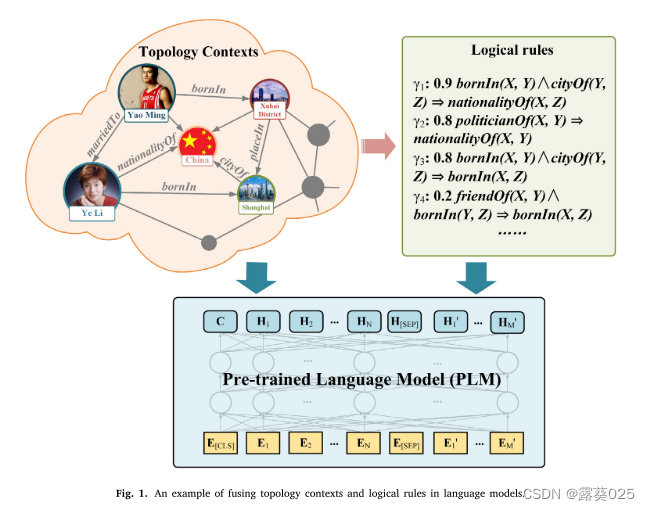
他们将实体的文本描述和三元组的关系输入LM中，以计算用于对该三元组的可扩展性建模的分数。它们只对三元组的局部信息进行建模，而忽略了KG中的长距离信息关联，例如，拓扑上下文和逻辑规则（参见图1中的示例）。拓扑上下文和逻辑规则对KGC都有重要作用，因为前者关注图的实体拓扑特征；后者强调关系之间的因果关联。

然而，在LM中融合拓扑上下文和逻辑规则是具有挑战性的。首先，知识生成器中的拓扑上下文以图的形式表示，这明显不同于语言模型所能处理的普通词序列。因此，不能使用LM直接对拓扑上下文建模。其次，知识群的逻辑规则由规则置信度和原子公式组成，包含关系和变量，表示抽象意义，例如，图1中的规则${\gamma }_1：0.9bornIn（X，Y）\wedge cityOf（Y，Z）\Rightarrow citynationalityOf（X，Z）$。将逻辑规则融合到LM中是困难的。一方面，知识生成系统中逻辑规则的谓词数量有限，规则的语义是通过谓词的置换来表达的；这与自然语言有很大的不同。因此，LM也不能直接对逻辑规则进行建模。另一方面，不存在具有语义置信度的标记逻辑规则作为LM的监督信息。

为了解决上述问题，我们提出了一种新的两阶段框架，隐式地表达KGC语言模型中的拓扑上下文和逻辑规则，称为FTL-LM。具体而言，对于拓扑上下文的学习，我们首先提出了一种异构随机行走算法，以产生多样化的拓扑路径，综合考虑各种因素，在KG中，包括广度优先采样，深度优先采样和不同的关系。通过省略中间实体，将这些拓扑路径转化为推理路径，并对其正反实例进行采样。然后，采用掩码语言建模和对比路径学习策略对拓扑路径和推理路径的语义信息进行建模。此外，引入软逻辑规则提取技术，将逻辑规则融合到逻辑模块中，利用两个结构相同但参数不同的逻辑模块分别进行三元组建模和规则建模。提出了一种变分期望最大化（EM）算法来迭代优化这两个LM。
在E-步骤中，三元组LM在观察到的三元组和有效的隐藏三元组的监督下更新，由固定规则LM验证。
在M步骤中，我们修复了三重LM并微调了规则LM以更新逻辑规则。
通过上述策略，知识群的拓扑上下文和逻辑规则都被隐式地融合在逻辑模型中。提出了一个融合逻辑模型中知识群拓扑上下文和逻辑规则的统一框架FTL-LM。据我们所知，这是第一个同时整合这两种信息的研究。

• 提出了一种基于路径的拓扑上下文学习方法，首先利用异构随机行走算法生成拓扑路径，然后构造推理路径及其正负样本。然后，利用掩码语言建模和对比路径学习来建模这些拓扑上下文的语义。
• 针对直接融合逻辑规则的困难性，引入变分EM算法，交替优化分别用于三元组建模和规则建模的两个LM。通过使用这种软蒸馏，KG的逻辑规则被纳入LM的第一次。
• 在两个常见的KGC数据集上的实验证明了我们的方法的优越性，这表明我们的FTL LM优于目前所有基于LM的方法。此外，消融研究证明了FTL-LM框架中每个模块的有效性。

本文的其余部分组织如下：第二部分介绍了KGC任务的相关工作。第3节给出了初步结果。我们提出的方法FTL-LM在第4节中详细介绍。第五部分对两种常用的KG进行了大量的实验和分析结果。最后，我们给予结论，并在第六节中讨论了未来的工作。

2 相关工作

目前，针对KGC任务的研究很多，主要分为四类：事实嵌入、拓扑嵌入、规则增强和基于LM的方法。

2.1 事实嵌入法

事实嵌入方法只考虑KG中以（h，r，t）形式的每个事实三元组作为基础。它们主要通过预设的三元组评分计算策略来优化随机初始化的实体和关系表示，其中平移距离模型和语义匹配模型是最具代表性的两种类型。平移距离模型通过特定关系平移后头实体和尾实体之间的距离来定义三元组得分。TransE 是这种类型的第一个也是最受欢迎的模型。它要求在向量空间R^d中加法运算的关系平移后，头实体表示接近尾实体，即 h + r ≈ t。基于TransE，已经提出了相关的方法并取得了巨大的成功，如TransH和RotatE。前者引入关系特定的超平面来扩展关系平移，后者将TransE在真实的空间中的加法运算转化为在复空间中从头实体到尾实体的旋转。

语义匹配模型通过嵌入空间中实体和关系向量的匹配度来表达三元组的有效性。例如，RESCAL为每个实体分配一个向量e∈R^d，为每个关系分配一个矩阵M∈R^d×d，以表示它们的内在语义。三重有效性由双线性函数定义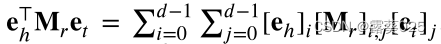：。DistMult 通过假设它是对角矩阵，即，𝐌 = diag®。基于DistMult，ComplEx将真实的空间中的嵌入向量转换为复杂空间，以更好地进行非对称关系建模。虽然这些事实嵌入方法简单有效，但它们只考虑KG的三重信息，导致建模不足和性能下降。

2.2 拓扑嵌入方法

为了更全面地嵌入KG信息，提出了几种基于GCN的拓扑嵌入方法。他们的策略是迭代地聚合从邻居节点到目标节点的信息，以集成本地拓扑结构。R-GCN是第一个将GCN应用于KG的工作，其中引入了关系特定矩阵来处理边缘的异质性。同时，提出了基分解和块对角分解，以避免过参数化和过拟合。此外，VRGCN和CompGCN 同时学习多关系KG的实体和关系的嵌入。CompGCN采用了多种实体-关系组合操作，效率很高，可以推广到多种多关系GCN方法。一般来说，这些方法已经取得了优异的性能，并被广泛使用，因为它们能够建模的知识库的拓扑上下文。然而，这类工作不能有效地处理实体和关系的内在语义。此外，对KG中的高级语义关联（例如，逻辑规则）对于这些方法也是具有挑战性的。最后但并非最不重要的是，由于这些拓扑嵌入模型嵌入了固定数量的实体和关系，它们可以简单地处理静态KGC，其实体和关系在未来不会增加。这显著地缩小了它们的应用范围，因为为了实现知识渊博和最新的KG，三元组在真实的世界中不断地增长。

2.3 规则融合方法

规则融合方法主要是通过挖掘KG中关系和局部结构之间的语义关联来实现可解释的KGC。神经LP是第一个以端到端可微方式学习一阶逻辑规则的研究。它通过将推理任务编译成可微运算序列来建模规则的参数和结构。基于神经LP，DRUM 通过引入额外的空关系将规则学习和推理扩展到可变长度模式。通过这种方式，它可以学习更丰富的规则并进行更准确的推理。为了同时学习KG的拓扑上下文和逻辑规则，JSSKGE 采用图注意力网络来聚合实体的局部结构信息。然后，它利用软逻辑规则隐含在KG作为一个专家，以进一步纠正嵌入。它可以通过联合学习方法进行KGC和规则学习。由于KG的开放世界假设，上述一次性规则学习方法不能完全反映真实的情况。因此，一些迭代模型的规则学习和推理的建议。例如，pLogicNet在变分EM框架中结合了KG嵌入和规则学习。在E-步骤中，使用事实嵌入模型来推断缺失的三元组，而在M-步骤中，基于观察和预测的三元组来更新逻辑规则的权重。类似地，RNNLogic引入了规则生成器以及用于迭代优化的推理预测器。在每次迭代中，首先更新推理预测器以探索一些逻辑规则。然后，通过后验推理，由规则生成器和推理预测器选择高质量的规则。最后，在这些高质量规则的监督下更新规则生成器。一般来说，这些规则融合的方法有很大的应用潜力，由于其可解释的优势，但受到限制的规则学习的可扩展性。此外，它们通常很难与知识库的其他特征有效地结合起来，完成精确的推理。

2.4 基于LM的方法

为了更好地表达实体和关系的内在语义，提出了一些文本增强方法。这些方法通常在事实嵌入方法的基础上增加文本描述的表示。然后，它们通过联合学习策略进行优化，例如TEKE和DKRL。近年来，预先训练的语言模型，例如，BERT和RoBERTa在自然语言处理（NLP）任务中取得了巨大的成功。当然，他们可以转移到KGC任务。KG-BERT 将头实体、关系和尾实体的文本描述连接起来作为BERT的输入，并将最终的[CLS]表示作为目标三元组的嵌入向量。然后，它被传递到一个双向分类器，以确定三元组是否合理。为了增强结构化知识在文本编码器中的表示，StAR将每个三元组划分为两个不对称部分，如基于映射的图嵌入方法，并将两个部分编码为上下文表示。然后采用确定性分类器和用于学习表示和结构的空间测量。然后，提出了基于线性矩阵的KGC多任务学习方法。例如，MTLKGC同时引入了链接预测，关系预测和相关性排名。LP-BERT为KGC进行多任务预训练，其中不仅利用了原始的掩码语言建模，还引入了掩码实体建模和掩码关系建模。这些方法都通过引入结构知识取得了很好的性能。然而，它们的建模结构仅限于三层，这未能捕获KG中的长距离结构语义，例如，拓扑上下文和逻辑规则。

为了克服现有LM方法的不足，本文提出了一个融合LM中KG的拓扑上下文和逻辑规则的统一框架FTL-LM。它可以被看作是一个扩展的一般LM为基础的方法，另外还纳入了拓扑嵌入方法和规则融合方法的建模信息。不同于传统的拓扑嵌入方法，利用GCN，我们提出了一种新的基于路径的方法学习的拓扑上下文使用LM。此外，在规则融合中，引入变分EM算法，交替优化分别用于三元组建模和规则建模的两个LM。这些具体的改进使得LM间接地达到了融合拓扑上下文和逻辑规则的目的。

3 准备

3.1 知识图谱和拓扑上下文

知识图可以形式化地表示为：G = {E，R，T_o}，其中E和R分别表示实体和关系的集合。T_o⊂ E × R × E 是观察到的三元组。由于开放世界假设（OWA）指出KG只包含真事实，未观察到的事实可能是假的或只是缺失的，因此存在有效的隐藏三元组，我们将其形式化为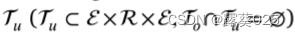。实体和关系的文本描述可以被视为和，其中| ⋅ |表示元素的数量。s^e_i和s^r_i是单词标记和单词标记是由不同数量的单词标记组成的句子，即，𝑠_𝑖= [𝑤₁,𝑤₂,𝑤_𝑛]。

在KG中有两种主要类型的拓扑上下文：局部和长距离拓扑上下文。局部拓扑上下文表示实体的最基本的图特征，其可以通过处理以（h，r，t）形式的三元组来建模。虽然一些事实模板方法使用这种拓扑实现了很好的性能，但它们不足以对KG的综合语义进行建模。长距离拓扑上下文模型用于KG中的较长拓扑，例如图1中的路径：（Yao Ming，marriedTo，Ye Li，Jiangsu In，Shanghai，placeIn，China）。它具有更复杂、更丰富的语义。为了更精确的KG嵌入，需要两种类型的拓扑上下文。

3.2 KG中的逻辑规则

一般逻辑规则通过蕴涵符号将前提和假设之间的因果关系联系起来，即，前提⇒假设。前提和假设都是由原子组成的，原子是通过谓词连接变量或常数的事实。由于KG结构的特殊性，我们引入了Horn规则，因为它易于处理和表达。Horn规则中的每个原子被表示为连接两个变量的谓词（KG中的关系），例如，bornIn(X , Y)。同时，它将前提限定为一组原子，将假设限定为一个原子，分别称为规则体和规则头。此外，为了方便而不失一般性，封闭Horn规则要求其规则体通过共享变量传递连接，其中第一个和最后一个变量与规则头的对应物相同。为了对不确定性进行建模，通常为每个Horn规则引入置信度 𝜖∈ [0 , 1]。规则的长度是规则体中的原子数。长度为2的封闭Horn规则示例如下所示：

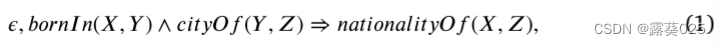
其中boinIn(X, Y) ∧ cityOf(Y, Z)是规则体，nationalityOf（X，Z）是一个规则头。通过将这些变量替换为KG中的具体实体，我们可以得到与原始Horn规则相对应的基本Horn子句。例如，规则（1）的基本Horn子句可以是：$bornIn（YaoMing，Shanghai）\wedge cityOf（Shanghai，China）\Rightarrow nationalityOf（YaoMing，China）$。

方程的后半部分表示添加新关系和实体后的信息转换。通常，用于拓扑路径生成的异构随机行走算法可以被概括为算法1。通过这种方式，我们收集了采样拓扑路径，它可以隐式地反映KG的长距离拓扑上下文。因此LM可以通过对这些路径进行建模来学习拓扑上下文。我们进行了两个任务的联合优化：掩码语言建模和对比路径学习。

掩码语言建模。对于长度为1的拓扑路径 ，我们将所有实体和关系替换为相应的文本描述作为LM的输入，即，

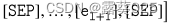
其中[𝚂𝙴𝙿]表示划分符号。[e_i]和[r_j]表示实体e_i和关系r_j的词序。为了对这些拓扑路径进行建模，我们利用word masking策略来微调KG上的LM。word masking首先在BERT中提出，以学习语义表示。为了使LM能够对KG的拓扑上下文进行建模，关系的整个词或实体的前几个词被选择性地屏蔽。我们每次选择一个实体的文本（除了拓扑路径中的第一个和最后一个实体）或一个关系进行掩码，直到所有掩码词达到拓扑路径中的15%标记。类似于BERT，80%的掩码词被替换为[𝙼𝙰𝚂𝙺]标记，10%被替换为随机标记，其余保持不变。

对比路径学习。上述掩码语言建模仅考虑KG的现有路径。为了进一步反映嵌入中的真实的或不存在的拓扑上下文，我们进行了对比路径学习，以保持语义信息。为了实现这一点，首先，我们限制了上述掩码语言建模的实现。每个拓扑路径分为两个部分：头部和尾部$e_{l+1}$。我们只屏蔽头部的实体或关系，不包括第一个和最后一个项目，即例子中的e₁和r₁。

然后，我们介绍了拓扑路径头部的推理路径，它只保留第一个实体，省略了其他中间实体，即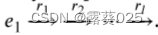，。事实上，这种形式的推理路径所表示的信息在很大程度上等价于相应拓扑路径的头部，因为后者可以通过前者在KG中的迭代推理来获得。此外，通过这样的转换，逻辑规则的置信度可以有效地由LM计算，这在4.2节中详细描述。通过在推理路径上的迭代推理，可以获得最后一个实体（推理尾），即，$e_{l+1}$。从这个角度来看，我们定义了正对比实例的锚推理路径：两者共享的主要拓扑上下文，并有相同的推理尾巴。我们可以通过一个简单的策略来实现这一点，即丢弃原始路径的一些开始部分。这样，正对比实例可以是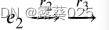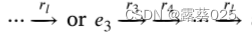。对于负对比实例，我们用一个随机关系替换锚推理路径中的一个关系，以确保新路径不会出现在KG中。例如，将r₂更改为另一个关系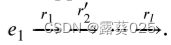：。因此，在一个否定的对比实例中，迭代推理不能到达原始的推理尾。

因此，我们引入其对数似然的证据下界：

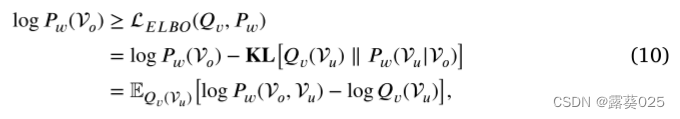
其中，$Q_v(V_u)$是潜变量的变分分布$V_u$。KL表示KL散度，并且当KL散度为0时等式成立，即，变分分布等于真后验分布：$Q_v(V_u=P_w(V_u|V_o))$。为了训练这个目标，我们遵循变分EM算法的策略，从两个步骤：E步和M步引入三元组LM_v迭代和规则LM LM_w迭代。

E步骤：推理程序。在推断的E步骤中，𝑃_𝑤 通过𝑄_𝑣最小化变分分布𝑄_𝑣(V_𝑢)和真实后验分布𝑃𝑤(V_𝑢|V_o)之间的KL发散来进行优化。𝑄_𝑣(V_𝑢)用平均场近似给出：

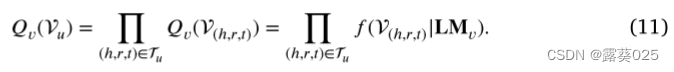
𝐋𝐌_𝑣表示用于推断三元组的可扩展性的三元组LM。通过最小化KL散度，可以通过以下方式计算最优的最小化：

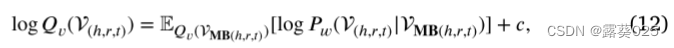
其中，c 是一个常量，MB(h, r, t)表示(h, r, t)的Markov blanket，这是在所有规则基础中与（h，r，t）一起出现的三元组。为了实现上述目标，我们首先计算𝑃_𝑤(V_(h,r,t)|V_MB(h,r,t))使用具有学习规则的MLN。然后，利用最小二乘法计算三元组的可达性，并在MLN输出的监督下进行优化。同时，为了保留现有的知识，KG在训练集上，我们还将观察到的三元组添加到训练集中。𝐋𝐌_𝑣总的来说，损失函数可以形式化地表示为：

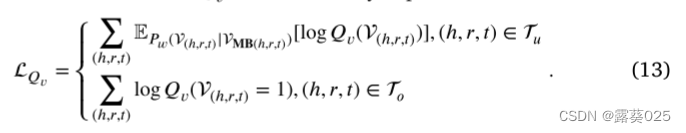
M-Step：学习程序。在M-步骤中，目标是学习具有固定阈值的逻辑规则的语义置信度，其最大化所有三元组的对数似然函数，即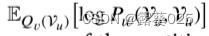。然而，由于配分函数的存在，直接优化是困难的。在我们的模型中，逻辑规则的置信度是通过一个非常离散的形式计算的，如Eq。(8)展示的那样。如果模型直接通过反向传播进行优化，这将导致大量的内存和计算开销。实际上，规则置信度是通过计算推理路径之间的相似度来获得的。因此，我们可以通过拓扑上下文学习的相似策略间接优化规则LM的模型，因为它通过对比学习来构建推理路径之间的语义关联。为了反映先验知识的训练，我们的样本的训练路径集的监督下的训练路径集的训练。𝑄𝑣以这种方式，可以通过以下损失函数来优化模型损失，该损失函数与Eq.(7)：

4.3 三元组嵌入

在这一节中，我们将介绍如何实现数据挖掘来获取事实三元组的局部上下文。具体而言，对于三元组（h，r，t）建模，平移距离方法的策略是通过测量空间距离来进行结构学习。他们定义了一个得分函数，比如三元组的得分函数为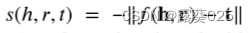$f(h,t)$是一个头嵌入和一个关系嵌入的组合函数，即transE中的$f(h,t)$ = 𝐡+𝐫

为了获得候选规则，使用类似于AMIE+的蛮力搜索来获得封闭的Horn规则。标准置信度是规则体基础数与规则基础数的商，用于过滤。进一步地，我们可以将隐藏的三元组T_u缩小到这些规则可以推导的部分，这大大减少了模型的计算量。在FTL-LM的拓扑上下文学习、三元组嵌入和规则学习过程中，推理路径都被用作建模对象的输入。虽然它们的生成方法和具体目的不同，但都是直接输入到LM中，然后通过余弦度量计算语义相似度。通过这种一致的计算过程，我们融合了KG的拓扑上下文和逻辑规则到LM中。FTL-LM的整个过程总结在算法2中。

在我们的LM-FTL中，我们利用与pLogicNet相似的策略进行软规则提取。但是，它们的实现方式完全不同。一方面，pLogicNet在E-step中使用简单的嵌入方法来建模三重有效性，例如TransE和DistMult。该方法是通过引入LM而实现的，不需要附加参数。另一方面，LM-FTL通过比较推理路径来计算规则置信度，并使用包含有效隐藏三元组的新生成路径来更新它们。但是pLogicNet只是通过梯度下降进行更新，梯度下降是由预测值和标记值计算的。

5 实验和结果

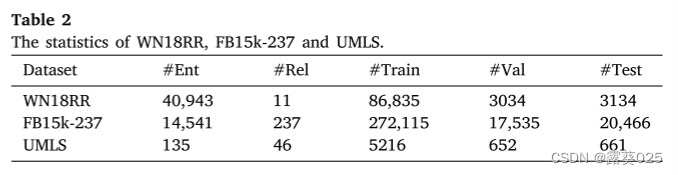
5.1 数据集和评价指标

我们对三种流行的KG进行了实验，即，WN 18 RR、FB 15 k-237和UMLS。WN 18 RR是WordNet的一个子集，由英语短语及其语义关系组成。FB 15 k-237来自Freebase ，它包含了真实的世界的大量事实。UMLS包含医学语义实体及其关系，可以看作是广泛用于KGC任务的域KG。所有这些都是具有挑战性和最受欢迎的基准。有关的统计数字载于表2。