[ 一刷完结撒花!! ] Day50 力扣单调栈 : 503.下一个更大元素II |42. 接雨水 | 84.柱状图中最大的矩形
Day50 力扣单调栈 : 503.下一个更大元素II |42. 接雨水 | 84.柱状图中最大的矩形
- 503.下一个更大元素II
- 第一印象
- 看完题解的思路
- 实现中的困难
- 感悟
- 代码
- 42. 接雨水
- 第一印象
- 看完题解的思路
- 暴力解法
- 单调栈解法
- 实现中的困难
- 感悟
- 代码
- 84.柱状图中最大的矩形
- 第一印象
- 看完题解的思路
- 感悟
- 代码
503.下一个更大元素II
这道题和 739. 每日温度 几乎如出一辙,可以自己尝试做一做
https://programmercarl.com/0503.%E4%B8%8B%E4%B8%80%E4%B8%AA%E6%9B%B4%E5%A4%A7%E5%85%83%E7%B4%A0II.html
第一印象
好, 那我就自己试试.
做出来了.
之前的单调栈题目就是遍历一遍数组, 找这一遍里右面最大的那个.
这道题说是循环数组, 其实也就是找两圈这个数组.
比如 5 2 3. 5是比3大的, 第一圈里只能找出3比2大, 第二圈才能找到5比3大.
有两个方式我觉得, 一个是找两圈数组, 也是我下面代码写的.
或者直接改造这个数组, 变成自己的两倍大小, 元素是自己的两遍, 比如5 2 3 5 2 3.
我自己写的代码,请看vcr:
class Solution {
public int[] nextGreaterElements(int[] nums) {
int[] result = new int[nums.length];
Deque<Integer> stack = new LinkedList<>();
int loop = 1;
Arrays.fill(result, -1);
stack.push(0);
for (int i = 1; i < nums.length; i++) {
if (nums[i] <= nums[stack.peek()]) {
stack.push(i);
} else {
while (!stack.isEmpty() && nums[i] > nums[stack.peek()]) {
//弹出栈顶元素,是下标
int index = stack.pop();
//记录结果
result[index] = nums[i];
}
stack.push(i);
}
if (loop == 1 && i == nums.length - 1) {
//因为循环结束 i++, 而第二圈应该从 i=0 开始.
i = -1;
loop--;
continue;
}
}
return result;
}
}
看完题解的思路
确实, 就是我上面说的两种方式, 但是扩大数组的复杂度就是O(n)了
而走两圈的方式, 卡哥比我做的要聪明一些, 用 % .
其实我也想到了, 就是感觉容易混乱在数学里.
for(int i = 0; i < 2*size; i++) {
while(!st.empty() && nums[i % size] > nums[st.peek()]) {
result[st.peek()] = nums[i % size];//更新result
st.pop();//弹出栈顶
}
st.push(i % size);
}
实现中的困难
在我的代码里
if (loop == 1 && i == nums.length - 1) {
//因为循环结束 i++, 而第二圈应该从 i=0 开始.
i = -1;
loop--;
continue;
}
走两圈的逻辑, 应该让 i = -1 ,而不是 i = 0
因为for循环结束之后会有 i++ .
感悟
虽然麻烦了点, 但我还是做对了
代码
上面给出了.
42. 接雨水
接雨水这道题目是 面试中特别高频的一道题,也是单调栈 应用的题目,大家好好做做。
建议是掌握 双指针 和单调栈,因为在面试中 写出单调栈可能 有点难度,但双指针思路更直接一些。
在时间紧张的情况有,能写出双指针法也是不错的,然后可以和面试官在慢慢讨论如何优化。
https://programmercarl.com/0042.%E6%8E%A5%E9%9B%A8%E6%B0%B4.html
第一印象
想了一下, 感觉情况比较多
- 两边都比自己高, 选小的那个 - 自己 = 水
- 两边有一边比自己高, ??? 这种情况咋办呢
- 两边都没自己高, 没有水
看题解!
看完题解的思路
暴力解法
找到右边第一个比自己大的, 左面第一个比自己大的. 就能算出来自己这里有多少水. 硬暴力去算.
单调栈解法
对于单调栈, 前面的题目已经会了找右边更大的(栈元素递增), 右边更小的(栈元素递减).
那怎么找左边更大的呢? 我第一反应是逆序遍历数组.
可以, 但有更好的方式. 这道题就是找到三个柱子, 左边更大+自己+右边更大
自己就是栈顶元素, 拿来的元素 i 可能是右边更大的(不更大就push入栈了), 那左边更大的在哪?
其实就是栈顶下面的那个元素, 如图:
因为栈里是递增的, 我自己下面那个就是 我左面第一个更大的呀
太tm巧妙了!!!
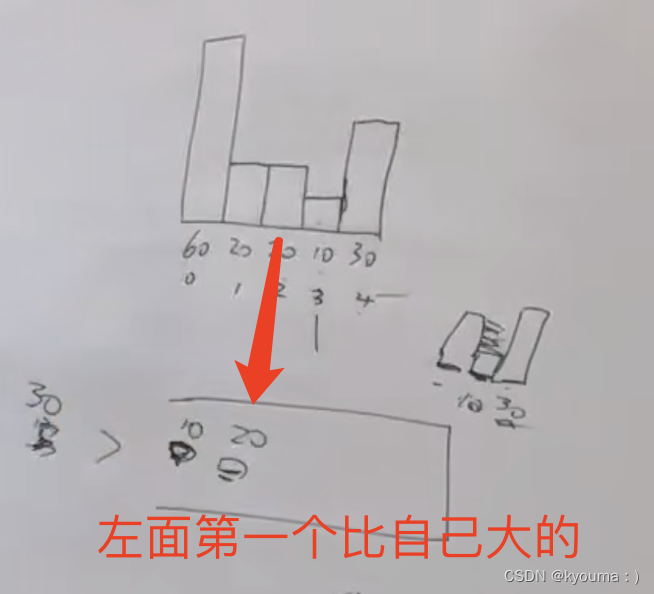
看完了, 会了
重要的是, 这道题是横向的求雨水面积, 我一直想的是 纵向的求雨水面积.
我听完题解还是觉得纵向的求没有错
但是细看
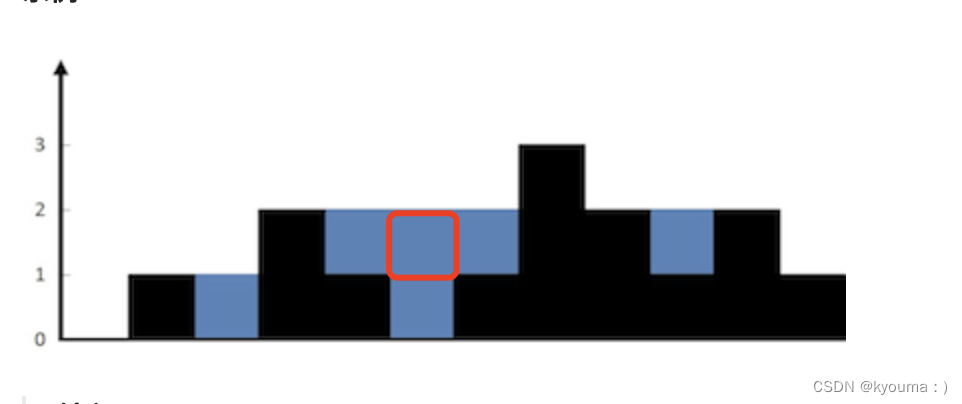
这个地方左面第一个更高和右边第一个更高最小的是 1
自己是 0
那么纵向雨水就是 1 , 算不到红色方块那里的
实现中的困难
思路清晰就不难实现
感悟
确实比较难
一个是纵向和横向计算容易糊涂
我也觉得横向计算的话, 下图的两个地方不会重复吗?
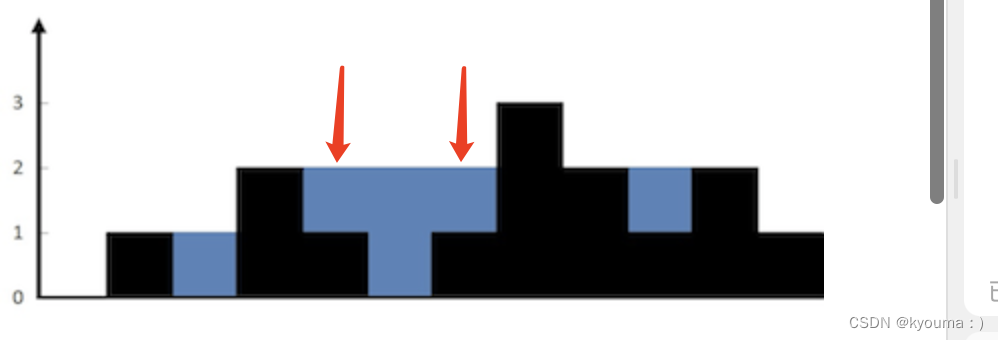
不会的
因为第二个 1 拿来的时候, 就比 0大了, 就会进行一次计算.
算出雨水量 1, 并把 0 pop掉, 第二个 1 push进去
拿来 3 的时候, 比栈顶的第二个 1 更大, 就会进行一次计算.
但是栈顶下面的元素就是第一个 1 , 在计算高度的时候, 取第一个 1 和 3 更小的那个 再减去栈顶的第二个 1 . 高度就是0 , 就白计算了.
然后第二个 1 pop
这个时候栈顶是第一个 1 , 栈顶下面的元素是 2 , 就会进行一次计算.
算出 高度 1 ,宽度 3, 雨水量 3.
然后pop掉第一个 1, 3 比栈顶的 2 还要大. 但是呢, pop 2 之后, 栈就空了, 就不会计算, 只是 pop 了2.
最后 3 push进栈, 再去算后面的元素.
顿悟 咯~~~~~~~~~~~~~
代码
class Solution {
public int trap(int[] height) {
int result = 0;
Deque<Integer> stack = new LinkedList<>();
stack.push(0);
for (int i = 1; i < height.length; i++) {
if (height[i] < height[stack.peek()]) {
stack.push(i);
} else if (height[i] == height[stack.peek()]) {
stack.pop();
stack.push(i);
} else {
while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
int curIndex = stack.pop();
int cur = height[curIndex];
//如果还有左边的话
if (!stack.isEmpty()) {
int min = Math.min(height[i], height[stack.peek()]);
//求高度
int h = min - cur;
int w = i - stack.peek() - 1;
//我纵向的求
int rain = w * h;
result += rain;
}
}
stack.push(i);
}
}
return result;
}
}
84.柱状图中最大的矩形
https://programmercarl.com/0084.%E6%9F%B1%E7%8A%B6%E5%9B%BE%E4%B8%AD%E6%9C%80%E5%A4%A7%E7%9A%84%E7%9F%A9%E5%BD%A2.html
今天是训练营最后一天,恭喜坚持两个月的录友们,接下来可以写一篇自己
代码随想录一刷的总结。好好回顾一下,这两个月自己的博客内容,以及自己的收获。
第一印象
我也觉得是要找左右两边第一个更小的
题解也是这么写的.
但是为啥呢
我只是有一种直觉, 它不像接雨水那样比较直观.
看完题解的思路
我明白了, 拿题里的例子说明一下
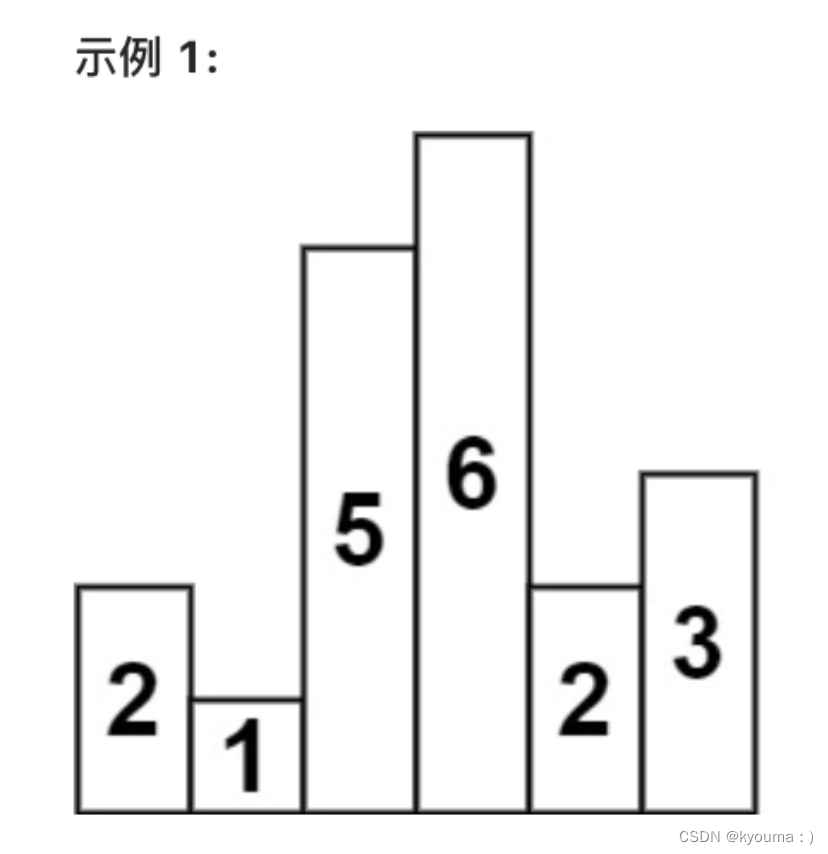
比如拿到元素 1 , 向左找第一个更小, 没有. 向右找第一个更小, 没有.
所以 1 的高度, 贯穿整个数组.
比如拿到 5, 向左找第一个更小是 1 . 向右找第一个更小, 是2.
那么 5 的高度就是从 1 贯穿到 2, 宽度其实就是 2 的下标 - 1 的下标 - 1.
这就是为什么要向左向右找第一个更小的原因.
也就是看现在这个元素(是高度)能贯穿多长(宽度).
然后这道题还有个处理技巧, 给数组扩容, 头和尾都加上高度 0 .
这样就方便算头和尾的元素的面积. 而且还能算出那个 最矮 的 1 的面积. 如图

但这里又会产生一个问题
对于相等的情况我自己写的时候的处理是, 什么都不做
if (heights[i] > heights[stack.peek()]) {
stack.push(i);
} else if (heights[i] == heights[stack.peek()]) {
//不处理, 相同的话先放进来的元素会让面积更大
} else {
比如 1 4 4 3.
肯定是第一个 4 算出的面积更大, 第二个 4 就是 4*1, 第一个 4 是 4 * 2.
所以遇到相同元素, 什么都不做就行了.
但是由于头加了 0 , 如果第一个高度还是 0的话就会出现错误.

扩容之后的数组是 0 0 9 0
因为相同元素什么都不干, 所以第二个 0 不会压入栈

这样计算 这个 9 的时候, 宽度就是 2 了. 就错了!!!
所以不能让相同元素什么都不干.
而是像接雨水一样, pop 在push 可以, 只push 也可以
还拿 1 4 4 3 的例子
pop 再 push, 栈顶就是第二个 4 , 下面是 1 . 拿到元素 3 的时候, 计算的宽度也是 3 - 0 - 1 = 2. 算的是到 1 到 3 的宽度. 是大的那个.
只push呢, 栈顶是第二个4 然后第一个4, 然后是 1 . 就是先算一个小的面积, 再算大的.
都是对的, 就是什么都不做不行.
感悟
这题也挺奇妙, 但是栈里递增递减不是什么难的.
主要就是头和尾 + 0 的小技巧
代码
class Solution {
public int largestRectangleArea(int[] heights) {
int maxArea = 0;
Deque<Integer> stack = new LinkedList<>();
// 数组扩容,在头和尾各加入一个元素
int [] newHeights = new int[heights.length + 2];
newHeights[0] = 0;
newHeights[newHeights.length - 1] = 0;
for (int index = 0; index < heights.length; index++){
newHeights[index + 1] = heights[index];
}
heights = newHeights;
stack.push(0);
for (int i = 1; i < heights.length; i++) {
if (heights[i] > heights[stack.peek()]) {
stack.push(i);
} else if (heights[i] == heights[stack.peek()]) {
stack.pop();
stack.push(i);
} else {
while (!stack.isEmpty() && heights[i] < heights[stack.peek()]) {
int curIndex = stack.pop();
int cur = heights[curIndex];
if (!stack.isEmpty()) {
int weight = i - stack.peek() - 1;
int area = cur * weight;
System.out.println(area + "=" + cur + "*" + weight);
maxArea = Math.max(maxArea, area);
}
}
stack.push(i);
}
}
return maxArea;
}
}
