电机应用开发-PID控制器参数整定
PID控制器参数整定
比例调节:调节作用快,系统一出现偏差,调节器立即将偏差放大输出。
积分调节:输出变化和输入偏差的积分成正比。输出不仅取决于偏差大小,还取决于偏差存在的时间。只要有偏差存在,尽管偏差可能很小,但它存在的时间越长,输出信号就越大。只有消除偏差,输出才停止变化。
微分调节:输出与被调量的变化率成正比。微分调节越大,越能提前响应,但是也会将不必要的偏差放大。
PID控制器参数整定的方法主要分为两大类:理论计算整定方法和工程整定法(经验法)。
理论计算整定方法主要是建立数学模型,然后根据数学模型经过理论的计算来确定最终的控制器参数。这种方法在所有的情况下都是理想的,经过这种方法调出来的参数是不可以直接使用的。
过程整定法主要是依赖于工程中的经验,直接在实际的控制系统的实验中进行。方法简单容易掌握,被广泛使用。
以经验法展开。
试凑法
采样周期的选择:要根据所设计的系统的具体情况,用试凑的方法,在试凑过程中根据各种合理的建议来预选采样周期,多次试凑,选择性能较好的一个作为最后的采样周期。
找整定参数时必须要认真的观察系统的相应情况,根据系统的响应情况来调整参数。
先P,再I,后D。调试时,将PID参数置于影响最小的位置,即P最大、I最大、D最小。
按纯比例系统整定比例系数,使其得到比较理想的调节过程曲线,然后再把比例系数放大1.2倍左右。然后将积分时间从小到大改变,使其得到较好的调节过程曲线。
然后在这个积分时间下重新改变比例系数,再看调节过程曲线有无改善。如有改善,可将原整定的比例系数减小,再改变积分时间,多次循环测试,就能得到合适的比例系数和积分时间。
如果在外界干扰下系统稳定性不好,可把比例系数和积分时间适当增加一点,使系统足够稳定。
将整定好的比例系数和积分时间适当减小,加入微分作用,以得到超调量(曲线最高点和目标线的差值)最小、调节作用时间最短的调节过程。
临界比例法
适用于闭环控制系统。
临界比例法:将调节器置于纯比例的作用下,从大到小逐渐改变调节器的比例系数,并且得到等幅度的震荡过程,此时为临界比例系数。
将调节器的积分置于最大,微分置于0,比例系数适当。
然后将比例逐渐增大,增大到产生等幅现象,并记录等幅时的临界比例系数和两个波峰的时间间隔。
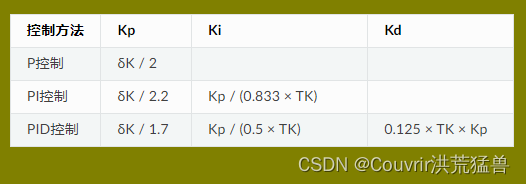
根据记下的比例系数和周期,采用经验公司,计算调节器的参数。
一般调节法
Kp是加快系统响应速度,提高系统的调节精度;Ki用于消除稳态误差;Kd改善系统的稳态性能。
PID调试一般原则(任何参数过大都会造成系统的振荡):
在输出不振荡时,增大比例增益P。
在输出不振荡时,减小积分时间常数Ti。
在输出不振荡时,增大微分时间常数Td。
确定P、I、D参数的一般步骤:
确定比例增益P:
首先去掉PID的积分项和微分项,一般是令Ti=0、Td=0,使PID为纯比例调节。
输入设定为系统允许的最大值的60%~70%,由0逐渐加大比例增益P,直到系统出现振荡。
然后在从此时的比例增益P逐渐减小,直到系统振荡消失。
记录此时的比例增益P,设定PID的比例增益P为当前值的60%~70%。比例增益P调试完成。
确定积分时间常数Ti:
比例增益P确定后,设定一个较大的积分时间常数Ti的初值,然后逐渐减小Ti,直至系统出现振荡。
然后逐渐加大Ti,直到系统振荡消失。
记录此时的Ti,设定PID的积分时间常数Ti为当前值的150%~180%。积分时间常数Ti调试完成。
确定积分时间常数Td:
积分时间常数Td:
一般不用设定,为0即可。若要设定,与前面方法一致,取不振荡时的30%。
系统空载、带载联调,再对PID参数进行微调,直至满足要求。
采样周期选择
采样周期越短,控制的效果越接近于连续,对于大多数算法缩短采样周期可使控制回路性能改善,但采样周期缩短时,频繁的采样会占用较多的计算工作时间,同时也会增加计算负担,而对有些变化缓存的受控对象无需很高的采样频率即可满意地进行跟踪,过多的采样反而没有多少实际意义。