归并排序详解：递归实现+非递归实现（图文详解+代码）

归并排序

• 时间复杂度：O ( N * log_zN ) 每一层都是N,有log₂N层
• 空间复杂度：O（N），每个区间都会申请内存，最后申请的数组大小和array大小相同
• 稳定性：稳定

目前为止，稳定的排序有：插入、冒泡、归并

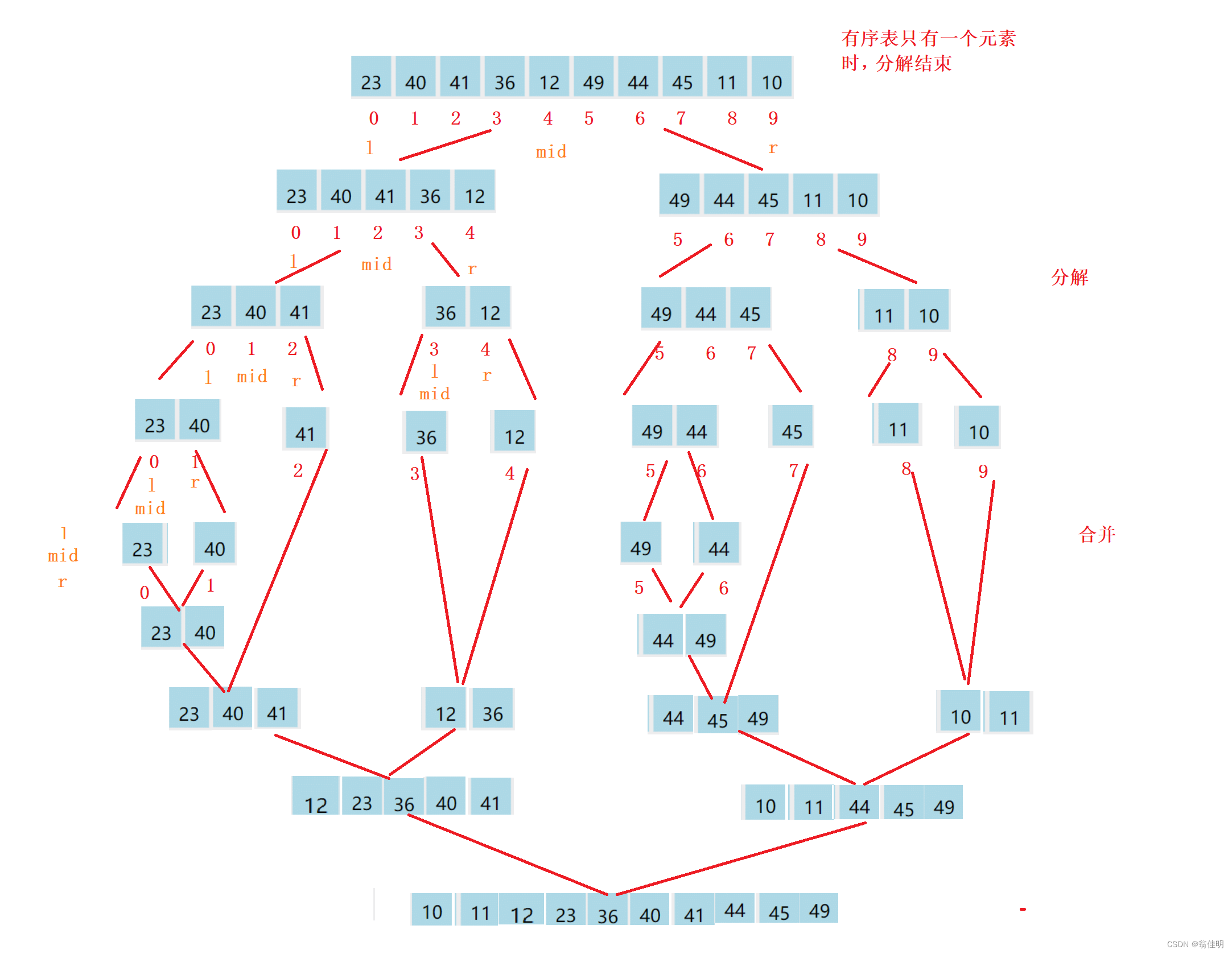
• 归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法，采用了分治法

• 将待排序列分解，先使每个子序列有序，再使子序列段间有序
• 将已有序的子序列合并，得到完全有序的序列
• 若将两个有序表合并成一个有序表，称为二路归并

1.递归实现

    /**
     * 归并排序
     * @param array
     */
    public static void mergeSort(int[] array) {
        mergeSortFunc(array,0,array.length-1);
    }

    private static void mergeSortFunc(int[] array, int left, int right) {
        //结束条件
        if (left >= right) {
            return;
        }
        //进行分解
        int mid = (left + right) / 2;
        mergeSortFunc(array, left, mid);
        mergeSortFunc(array, mid + 1, right);
        //左右分解完成后，进行合并
        merge(array, left, right, mid);


    }

    //进行合并
    private static void merge(int[] array, int start, int end, int mid) {
        int s1 = start;
        int s2 = mid + 1;
        int[] tmp = new int[end - start + 1];
        int k = 0;//k为tmp数组的下标
        while (s1 <= mid && s2 <= end) {//两个数组中都有数据
            //进行比较，放到新申请的数组
            if (array[s1] <= array[s2]) {
                tmp[k++] = array[s1++];
            } else {
                tmp[k++] = array[s2++];
            }
        }
        //因为有&&条件，数组不一定走完
        while (s1 <= mid) {
            tmp[k++] = array[s1++];
        }
        while (s2 <= end) {
            tmp[k++] = array[s2++];
        }
        //此时，将排好的tmp数组的数组，拷贝到array
        for (int i = 0; i < tmp.length; i++) {
            array[i+start] = tmp[i];//对齐下标
        }
    }

2.非递归实现

    /***
     * 归并排序，非递归实现
     * @param array
     */
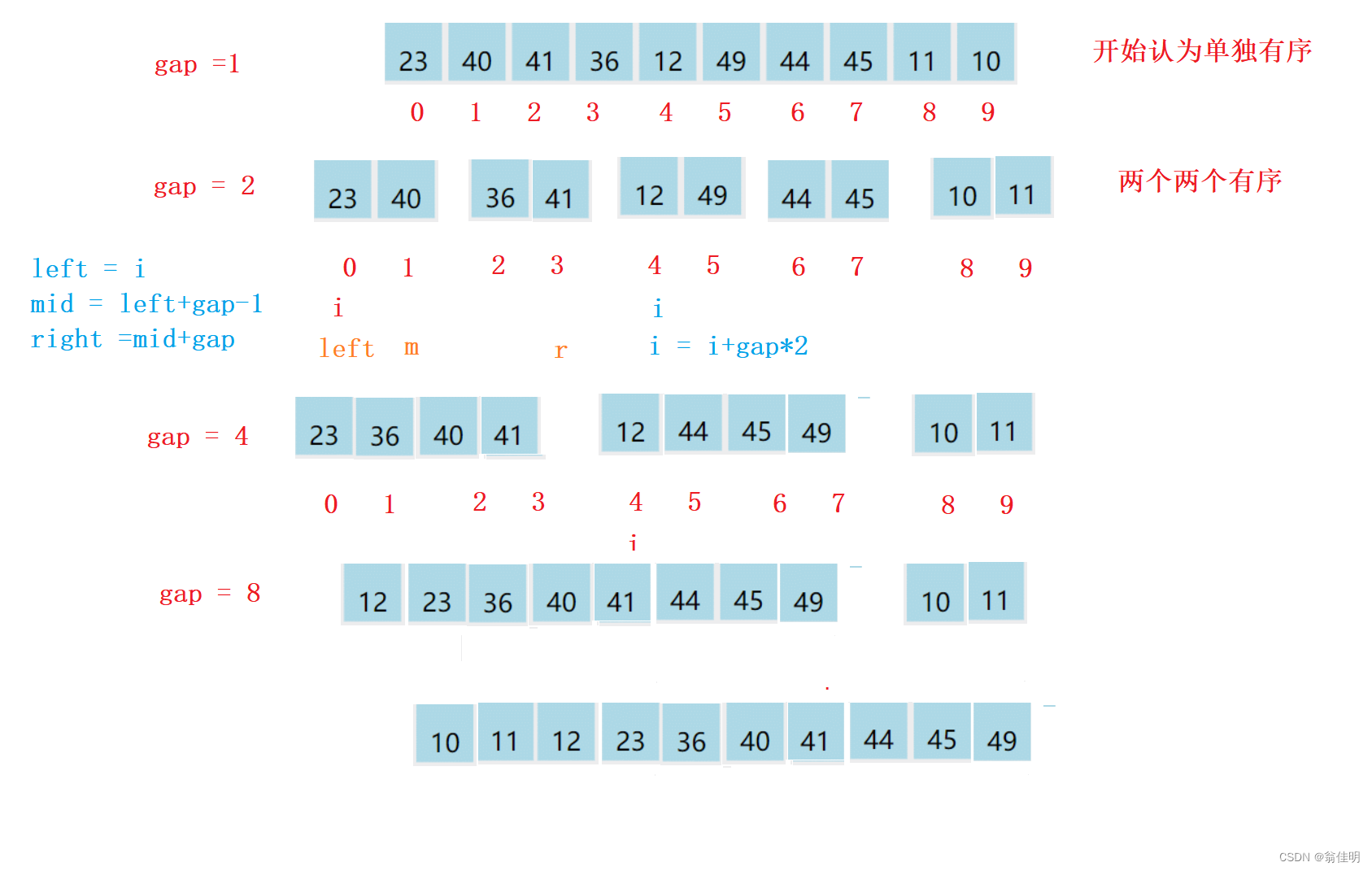
    public static void mergeSort2(int[] array) {
        int gap = 1;
        while (gap < array.length) {
            //i += gap * 2 i每次跳到下一组
            for (int i = 0; i < array.length; i += gap * 2) {
                int left = i;
                //要避免mid和right越界
                int mid = left + gap - 1;
                if(mid>=array.length){
                    mid = array.length-1;//修正越界的情况
                }
                int right = mid + gap;
                if (right>=array.length){//修正越界的情况
                    right = array.length-1;
                }
                merge(array,left,right,mid);//进行合并
            }
            gap *=2;//2倍数扩大组数
        }
    }
    //进行合并
    private static void merge(int[] array, int start, int end, int mid) {
        int s1 = start;
        int s2 = mid + 1;
        int[] tmp = new int[end - start + 1];
        int k = 0;//k为tmp数组的下标
        while (s1 <= mid && s2 <= end) {//两个数组中都有数据
            //进行比较，放到新申请的数组
            if (array[s1] <= array[s2]) {
                tmp[k++] = array[s1++];
            } else {
                tmp[k++] = array[s2++];
            }
        }
        //因为有&&条件，数组不一定走完
        while (s1 <= mid) {
            tmp[k++] = array[s1++];
        }
        while (s2 <= end) {
            tmp[k++] = array[s2++];
        }
        //此时，将排好的tmp数组的数组，拷贝到array
        for (int i = 0; i < tmp.length; i++) {
            array[i + start] = tmp[i];//对齐下标
        }
    }

点击移步博客主页，欢迎光临~