当前位置： 首页 > article >正文

栈和队列知识点+例题

article 2024/9/21 1:34:15

1.栈

1.1栈的概念及结构

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素的操作。进行数据插入和删除操作的一端成为栈顶，另一端成为栈底。遵守后进先出的原则（类似于弹夹）

压栈：栈的插入操作叫做进栈/入栈/压栈，入数据在栈顶

出栈：栈的删除操作叫做出栈，出数据也在栈顶

那如何实现栈呢？

 经过比较，数组栈是最优解，（链式的扩容会很久才会扩容一下）

由于top的位置意义不同，我们分为两种解决方案

1.2基本操作 

1.定义一个栈

typedef int SLDataType；
typedef struct Stack
{
    int *a;
    int top;
    int capacity;
}

2,初始化一个栈

void STInit(ST*pst)
{
     assert(pst);
    pst->a=NULL;
    pst->top=0;
    pst->capacity=0;
}

3压栈

void STPush(ST* pst, SLDataType x)
{
	assert(pst);
	if (pst->top == pst->capacity)
	{
		ST* newcapacity = pst->capacity == 0 ? 4 : capacity * 2;
		SLDataType* tmp = (SLDataType*)realloc((SLDataType)*newcapacity);
		if (newcapacity == NULL)
		{
			return -1;
		}
		else
		{
			pst->a = tmp;
			pst->capacity = newcapacity;
			pst->a[pst->top] = x;
			pst->top++;
		}
	}
}

 4，弹栈

void STPop(ST* pst)
{
    assert(pst);
    assert(pst->top>0);
    pst->top--;
}

5 返回栈顶元素

void STTop(ST* pst)
{
    assert(pst);
    assert(pst->top>0);
    return pst->a[pst->top-1];
}

6 判断是否为空

bool STEmpty(ST* pst)
{
	assert(pst);
	if (pst->top == 0)
	{
		return true;

	}
	else
	{
		return false;
	}
}

7 栈的大小

int STSize(ST* pst)
{
    assert(pst);
    return pst->top;
}

8销毁栈

void STDestory(ST*pst)
{
    assert(pst);
    free(pst->a);
    pst->a=NULL;
    pst->top=pst->capacity=0;
}

让我们看几道例题吧

例题1：

 思路：栈的顺序是后进先出，有题可知，最后一个是E，所以E先出，故选B

例题2：

 我们首先看选项，A选项：1先进，1先出，把2 3 4放进去，把4拿出来，再把3拿出来，最后把2拿出来。同理，我们看C选项，把1 2 3放进去，然后把3拿出来，然后我们会发现，如果想要拿1的话，拿2是必经之路，所以此选项错误

例题3：

 思路：

1，先建立一个栈，初始化一个栈，

2，然后我们把所有的左括号放入栈里面，如果不是左括号，即是有括号；

3，其次我们要知道，本题的关键在于数量匹配和顺序匹配。所以我们要考虑一下栈是否为空（右括号的数量大于左括号的数量），然后考虑顺序匹配的问题

4，最后我们看栈是否为空，如果为空，就返回true，然后把栈毁掉

bool isVaild(char* s)
{
	ST st;// 定义一个栈
	STInit(&st);
	while (*s)
	{
		if (*s == '[' || *s == '{' || *s == '(')
		{
			STPush(&st, *s);
			s++;
		}
		else
		{
			if (STEmpty(&st))
			{
				return false;
			}
			//栈里面取左括号
			char top = STTop(&st);
			STPop(&st);
			//顺序不匹配
			if (*s == ']' && top != '[') || (8s == '}' && top != '{') || (*s == ')' && top == '(')
			{
				return false;
			}
			s++;
		}
	}
	//栈为空，返回真，说明数量都匹配
	bool ret = STEmpty(&st);
	STDestory(&pst);
	return ret;
}

好啦~栈我们就先讲到这里啦，让我们看一下队列的知识点吧

2，队列

2.1队列的概念和结构

 我们可以考虑一个问题

入队之后，出队的时候顺序是唯一一定的吗？

答案是：当然是；

从以上我们可以了解到，栈用数组的方法比较好；而队列用单链表，头删尾插的方式比较好

2.2基本操作

1定义一个队列

typedef int QueueType;
typedef struct QueueNode
{
	QueueType val;
	struct QueueNode* next;

}QNode;

为了解决二级指针以及两个指针的问题，我们可以把两个指针放入一个结构体里面，然后进行一级指针的操作即可

typedef struct Queue
{
	QNode* phead;
	QNode* ptail;
	int size;
}Queue;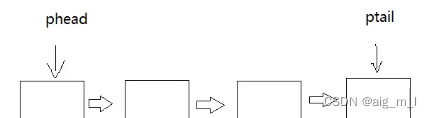

2.初始化一个队列

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->size = 0;
	pq->phead = pq->ptail = NULL;
}

3.插入到队列

	void QueuePush（Queue* pq, QDataType x)
	{
		QNode* newnode = (QNode*)malloc(sizeof(QNode));
		if (newnode == NULL)
			return -1;
		else
		{
			newnode->val = x;
			newnode->next = NULL;
		}
		if (pq->tail == NULL)
		{
			return -1;

			pq->tail = pq->phead = newnode;
		}
		else
		{
			pq->tail->next = newnode;
			pq->tail = newnode;
		}
		pq->size++;
	}

4. 头删

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	QNode* del = pq->phead;
	pq->phead = pq->phead->next;
	if (pq->phead = NULL)
		pq->tail = NULL;
}

5找头结点的值

QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	return pq->phead->val;
}

6队列是否为空

bool QueueEmpty(Queue* pq)
{
    assert(pq);

  return pq->phead=NULL;
}

7队列大小

int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

8销毁队列

void QueueDestory(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->phead;
	while (cur)
	{
		QNode* next = cur->next;
		cur = next;
	}
pq->phead=pq->ptail=NULL;
}

让我们看几道关于队列和栈的例题吧

例题1：

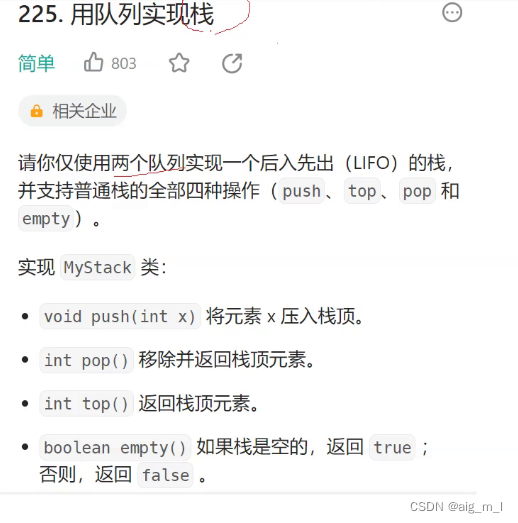
思路： 

 代码实现：

typedef struct
{
	Queue q1;
	Queue q2;

}Stack;

MyStack* CreateStack()
{
	MyStack* pst = (MyStack*)malloc(sizeof(MyStack));
	QueueInit(&pst->q1);
	QueueInit(&pst->q2);

	return pst;
}
void mystackpush(Mystack* obj, int x)
{
	Queue Empty = &obj->q1;
	Queue nonEmpty =&obj->q2;
	if (!Empty(&obj->q1))
	{
		Queue Empty = &obj->q2;
		Queue nonEmpty = &obj->q1;
	}
	//开始到数据
	while (QueueSize(nonempty) > 1)
	{
		QueuePush(Empty, QueueFront(nonempty));
		QueuePop(nonempty);
	}
	int top = QueueFront(nonempty);
	QueuePop(nonempty);
	return top;
}

int mystackTop(Mystack* obj)
{
	if (!Empty(&obj->q1))
	{
		return QueueBack(&obj->q1);
	}
	else
	{
		return QueueBack(&obj->q2);
	}
}
bool mystackEmpty(MyStack* obj)
{
	return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}
void mystackFree(Mystack* obj)
{
	QueueDestory(&obj->q1);
	QueueDestory(&obj->q2);
	free(obj);
}

例题2：

 

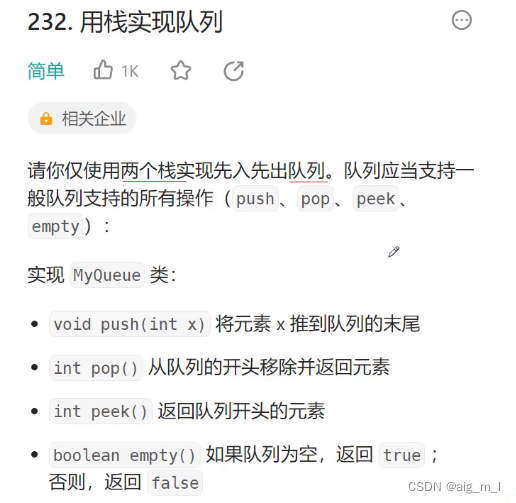
 思路：

 代码实现：

 

typedef struct
{
	int* a;
	int top;
	int capacity;
}ST;
typedef struct
{
	ST pushst;
	ST popst;
}MyQueue;
//初始化
void STInit(ST* pst)
{
	assert(pst);
	pst->a = NULL;
	pst->top = 0;
	pst->capacity = 0;
}
//压栈
void STPush(ST* pst, SLDataType x)
{
	assert(pst);
	if (pst->top == pst->capacity)
	{
		ST* newcapacity = (SLDataType*)malloc(sizeof(SLDataType);
		SLDataType* tmp = pst->capacity == 0 ? 4 : newcapacity * 2;
		if (newcapacity == 0)
		{
			return -1;
		}
		else
		{
			pst->a = tmp;
			pst->capacity = newcapacity;
			pst->a[pst->top] = x;
			pst->top++;
		}
	}
}
//返回栈顶元素
void STTop(ST* pst)
{
	assert(pst);
	assert(pst->top > 0);
	return pst->a[pst->top - 1];
}
//弹栈
void STPop(ST* pst)
{
	assert(pst);
	assert(pst->top > 0);
	pst->top--;
}
//判断是否为空
bool STEmpty(ST* pst)
{
	assert(pst);
	if (pst->top == 0)
	{
		return true;
	}
	else
	{
		return -1;
	}
}
MyQueue* myQueueCreate()
{
	MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));
	STInit(&obj->pushst);
	STInit(&obj->popst);
	return obj;
}
void myQueuePush(MyQueue* obj, int x)
{
	STPush(&obj->pushst, x);
}
返回队列开头的元素（不删除）
void myQueuepeek(MyQueue* obj)
{
	if (!STEmpty(&obj->popst))
	{
		return STTop(&obj->popst);
	}
	else
	{
		while (!STEmpty(&obj->pushst))
		{
			STPush(&obj->popst, STTop(&obj->pushst);
			STPop(&obj->pushst);
		}
		return STTop(&obj->popst);
	}
}
//从队列开头移除并返回元素
void myQueuePop(MyQueue* obj)
{
	int front = myQueuePeek(obj);
	STPop(&obj->popst);
	return front;
}
bool myQueueEmpty(MyQueue* obj)
{
	return  STEmpty(&obj->pushst) && (&obj->popst);
}
void myQueueFree(MyQueue* obj)
{
	STDestory(&obj->popst);
	STDestory(&obj->pushst);
	free(obj);
}

接下来我们看一下循环队列吧

1.判断循环队列是否为空：front==back（front指向对头，back指向队尾的下一个）

 

 如何判断队列是否为满

1.前提：front==back（当size=0时，为空，size！=0则为满）

2，再增加一个地方）

即

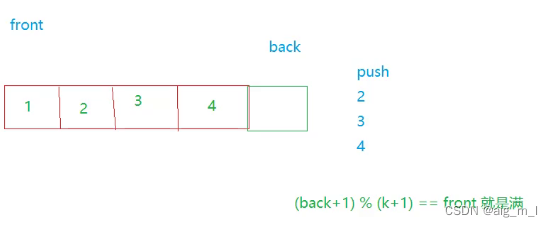
数组实现（back+1）%（k+1）==front则为满，其中，k+1指的是开辟空间的个数，k指的是有效数据数 数组实现&（k+1）是为了防止溢出

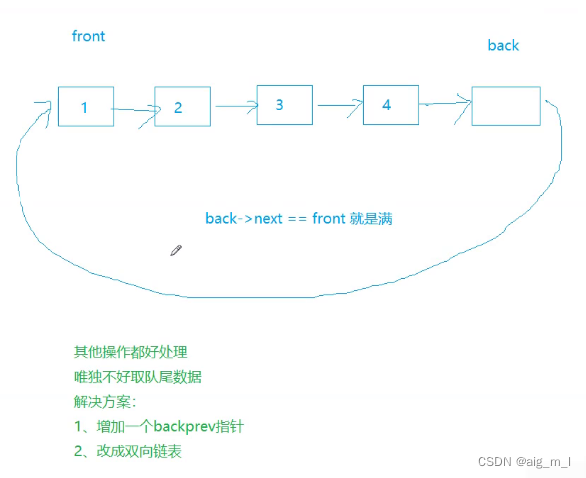
链表实现，即把上面式子去掉  %（k+1）

链表实现：

 

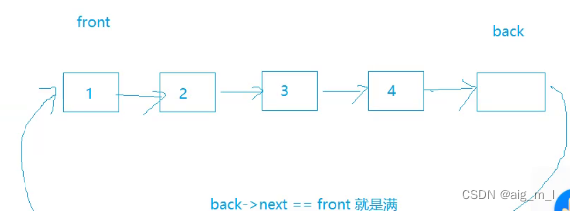
 数组实现：

 单链表缺陷以及找尾的办法：

 如何计算循环中元素的个数

typedef struct {
	int* a;
	int front;
	int back;
	int k;
}MyCircularQueue;
//初始化
MyCircularQueue* myCircularQueueCreate(int k) {
	MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
	obj->a = (int*)malloc(sizeof(int) * (k + 1));
	obj->front = 0;
	obj->back = 0;
	obj->k = 0;
	return obj;
}
//是否为空
bool myCircularQueueEmpty(MyCircularQueue* obj)
{
	return obj->front = obj - back;

}
//是否为满
bool myCircularQueueIsFull(MyCircularQueue* obj)
{
	return (obj->front) % (obj->k + 1) == obj->front;

}
//插入
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value)
{
	if (myCircularQueueIsFull(obj))
	{
		return false;
	}
	obj->a[obj->back] = value;
	obj->back++;
	obj->back % (obj->k + 1) = obj->back;
	return true;
}
//删除
bool myCircularQueueDeQueue(MyCircularQueue* obj, int value)
{

	if (myCircularQueueIsFull(obj))
	{
		return false;
	}
	++obj->front;
	obj->front % (obj->k + 1) = obj->front;
	return true;
}
//返回队头
int myCircularQueueFront(MyCircularQueue* obj)
{
	if (myCircularQueueIsFull(obj))
	{
		return false;
	}
	return obj->a[obj->front];
}
//返回队尾
int myCircularQueueRear(MyCircularQueue* obj)
{
	if (myCircularQueueIsFull(obj))
	{
		return false;
	}
	return obj->a[obj->back - 1];
}
//清空
void myCircularQueueFree(MyCircularQueue* obj)
{
	free(obj->a);
	free(obj);
}

好啦~关于栈和队列的知识点就这些啦~谢谢大家观看~


http://www.kler.cn/news/135653.html

相关文章：

  • 中国农业开启加速度，龙江农业迎来黄金期
  • 二阶段提交
  • thonny的汉字编码是UTF-8，如何才能转为GB2312?
  • LeetCode - 622. 设计循环队列（C语言，顺序存储结构，配图）
  • 逻辑漏洞（越权）
  • MySQL 的执行原理（五）
  • AI 游戏工具收集
  • 设计模式（二）-创建者模式（1）-单例模式
  • uniapp Android如何授权打开系统蓝牙Bluetooth？
  • 【ES6标准入门】JavaScript中的模块Module语法的使用细节：export命令和imprt命令详细使用，超级详细！！！
  • vue统一登录
  • C# 依赖注入如何实现
  • 数据结构【DS】栈
  • 音视频项目—基于FFmpeg和SDL的音视频播放器解析（十三）
  • 二维偏序问题
  • 从傅里叶变换，到短时傅里叶变换，再到小波分析（CWT），看这一篇就够了（附MATLAB傻瓜式实现代码）
  • 多维时序 | MATLAB实现PSO-BiGRU-Attention粒子群优化双向门控循环单元融合注意力机制的多变量时间序列预测
  • 毕业设计ASP.NET 2368酒店信息管理系统【程序源码+文档+调试运行】
  • 腐蚀监测常用技术及作用
  • 解决word之间复制公式时，公式编辑器变成图片
  • 【算法】堆排序
  • （BMS）电池管理系统技术研究与仿真
  • Selenium安装WebDriver最新Chrome驱动(含116/117/118/119)
  • 为什么阿里推荐 LongAdder ，不推荐 AtomicLong ？？
  • 蓝桥杯每日一题2023.11.20
  • WPF Visual, UIElement, FrameworkElement, Control这些类的区别
  • 【论文阅读】基于隐蔽带宽的汽车控制网络鲁棒认证（二）
  • 力扣刷题-二叉树-二叉树最小深度
  • 【STM32】RTC（实时时钟）
  • 13.真刀实枪做项目---博客系统(页面设计)