浅析RSA非对称加密算法

目录

引言

凯撒密码

对称加密

非对称加密

​编辑总结

引言

几月前在知乎上看到一个关于RSA公钥与私钥加解密的提问甚感兴趣，却一直没有时间去探究，今日浅得闲时以文记之。

在文章正式开始之前先讲一个小故事，在公元前58年时，凯撒带领他的军队征战四方，由于当时的通信手段远不及现代这样迅速便捷，书信甚至口头传文便是司空见惯的事情，即使在军队中也不例外。而这种方式带来的问题便是如何保证信息不泄露呢？对于当时的军队而言协同作战时信息泄露是非常可怕的事情，因此凯撒研究出了一种适用于当初场景下安全传输的方法，从而带领军队大获全胜。到底是什么样的方法使得凯撒在那个时期所向披靡呢？再往下看便会知道答案。

凯撒密码

引言中提到的便是著名的凯撒加密，凯撒加密的原理如下，通过使用字母表和一个偏移量v(密钥)，从而实现对明文信息的加密。需要注意的是这里的字母是循环的，即Z右移3位后便是C，以此类推。

举个简单的例子，如下为26个字母组成的明文字母表，与之对应的便是通过移位3次后获取到的密文。

明文字母表：ABCDEFGHIJKLMNOPQRSTUVWXYZ
密文字母表：DEFGHIJKLMNOPQRSTUVWXYZABC

根据上述规则，很快我们可以知道如下密文:

KHOOR,ZRUOG!

对应的原文便是:

HELLO,WORLD!

虽然凯撒密码在目前来看已经不具备任何的安全性，无法保护信息载体，但在其被应用的那个时代却是非常重要的存在，作为古典密码的代表之一，为后来的密码体系奠定了基础。除此之外，凯撒密码也可看做最为简单的对称加密算法。

对称加密

上一部分中提到了凯撒加密可以作为一个最为简单的加密算法，其原因是因为对称加密算法加密和解密使用了同样的密钥，与凯撒密码中的偏移量有异曲同工之妙。

对称加密算法的图示如下：

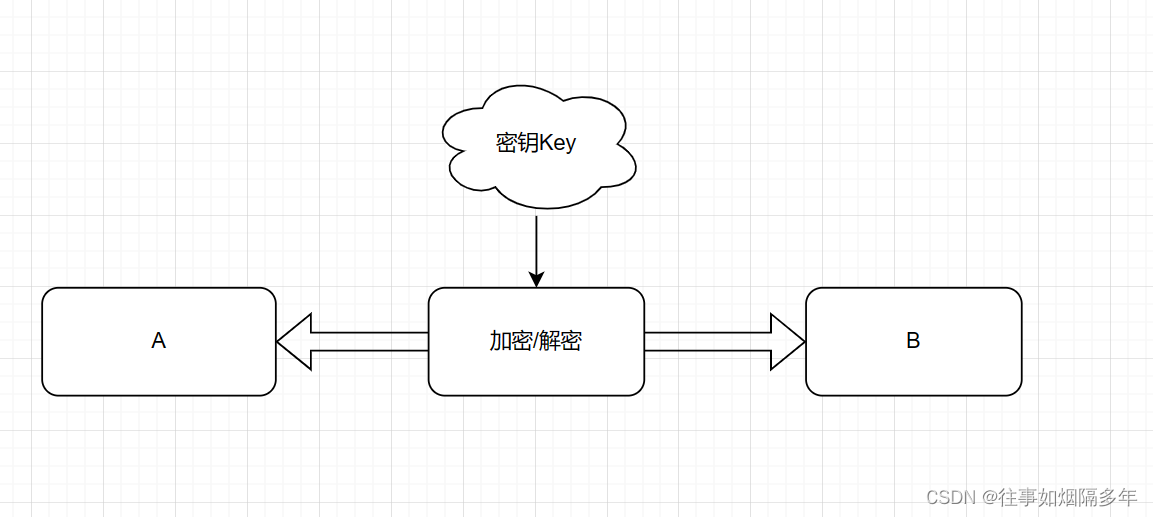
如图所示，对于通信双方A和B将使用同一个密钥来进行加密与解密，将明文数据通过密钥和加密算法结合后产生密文发送给B，B接收后通过相同密钥解出明文。

不难看出对称加密的特点是双方共用一个密钥，并且其加解密速度快，但与之而来的问题便是如果密钥Key泄露将导致通信双方的数据不再安全。

目前市面上较为主流的对称加密算法为AES，其除需要密钥Key外还需要使用一个偏移量iv，并且提供了多种的数据填充模式，本文不做过多赘述。

非对称加密

在了解了对称加密后，终于可以请出我们的今天的主角——非对称加密，相比于上述提到的对称加密，非对称加密的特点是加解密一对密钥对，准确来说一般我们都使用的是公钥加密，私钥解密。而由于大整数因式分解在目前难以实现，因此RSA的安全性较高，但相比于对称加密其效率较低。

这里提到的公钥和私钥是指在使用非对称加密算法情况下生成的密钥对，私钥一般均保存给自己所持有，公钥则可以给任何人，因为使用公钥加密后的密文只有私钥才能解，因此即使当密文被拦截时，攻击者由于没有私钥将无法解密从而获取内容。

因此当A与B想要进行通信时，可以通过B发送的公钥对消息进行加密，而B在收到消息后可以通过自己的私钥实现消息解密查看。

当然也有存在“私钥签名，公钥验签”这种说法，其依赖于消息摘要算法为基础以实现。

回到文章开头的问题，一般来讲为“公钥加密，私钥解密”，事实上私钥也可加密，但一般来说并不会这样做，由于私钥可以推出公钥使其安全性尽失，并且私钥泄露也使加密失去了意义。

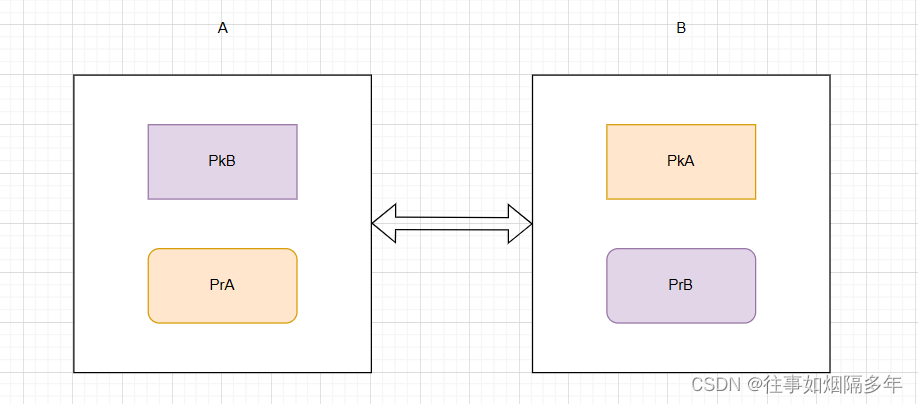
因此实际中使用RSA来加密通信信息时，事实上是通信双方各自生成了一对密钥对，双方通过交换公钥进而实现进一步通信。

总结

虽然RSA非对称加密算法提供了较高的安全性，但其性能却有所降低。本文所述以上场景为可信网络条件下，即不考虑诸如中间人攻击、公钥交换失败的情况，对于解决信息防篡改则需要引入消息摘要算法、数字签名作以辅助以确保数据的准确性和可靠性。