【数据结构】树与二叉树（廿五）：树搜索指定数据域的结点（算法FindTarget）

5.3.1 树的存储结构

5. 左儿子右兄弟链接结构

【数据结构】树与二叉树（十九）：树的存储结构——左儿子右兄弟链接结构（树、森林与二叉树的转化）
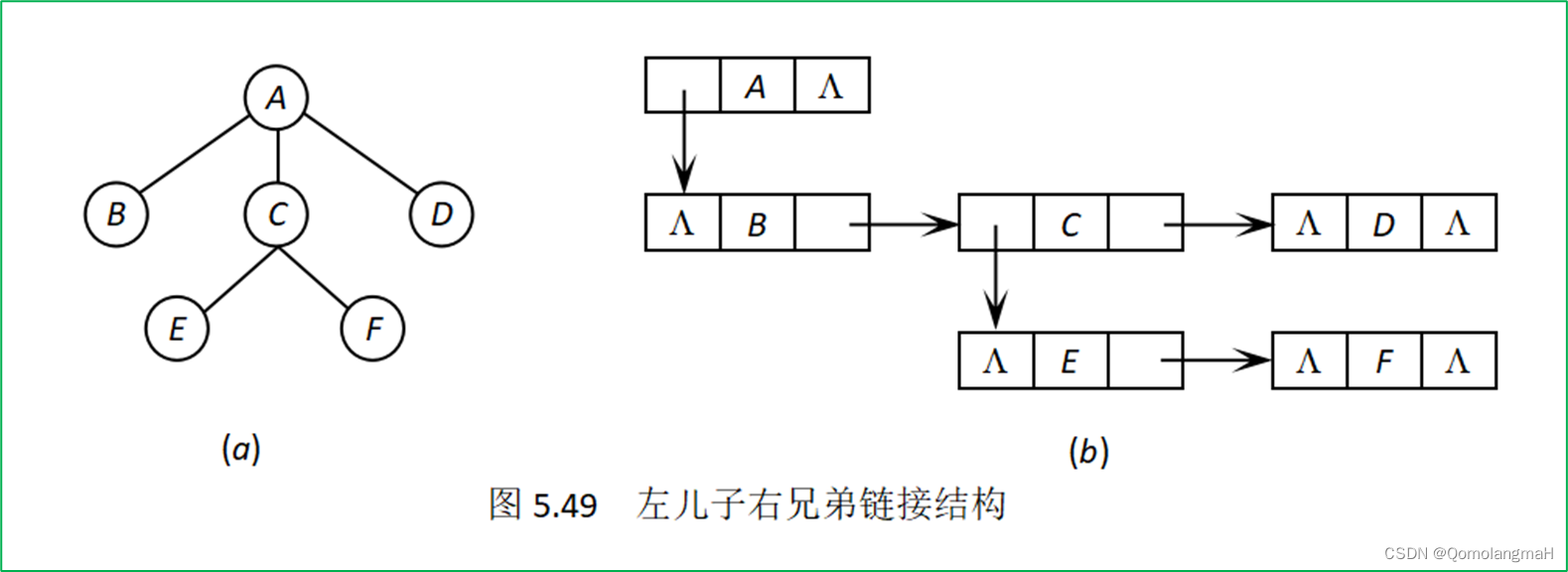
  左儿子右兄弟链接结构通过使用每个节点的三个域（FirstChild、Data、NextBrother）来构建一棵树，同时使得树具有二叉树的性质。具体来说，每个节点包含以下信息：

1. FirstChild： 存放指向该节点的大儿子（最左边的子节点）的指针。这个指针使得我们可以迅速找到一个节点的第一个子节点。
2. Data： 存放节点的数据。
3. NextBrother： 存放指向该节点的大兄弟（同一层中右边的兄弟节点）的指针。这个指针使得我们可以在同一层中迅速找到节点的下一个兄弟节点。

  通过这样的结构，整棵树可以用左儿子右兄弟链接结构表示成一棵二叉树。这种表示方式有时候被用于一些特殊的树结构，例如二叉树、二叉树的森林等。这种结构的优点之一是它更紧凑地表示树，而不需要额外的指针来表示兄弟关系。

   A
  /|\
 B C D
  / \
 E   F

A
|
B -- C -- D
     |
     E -- F

即：

      A
     / 
    B   
    \
	  C
  	 / \ 
  	E   D
  	 \
  	  F

5.3.2 获取结点的算法

1. 获取大儿子、大兄弟结点

【数据结构】树与二叉树（二十）：树获取大儿子、大兄弟结点的算法（GFC、GNB）

2. 搜索给定结点的父亲

【数据结构】树与二叉树（廿四）：树搜索给定结点的父亲（算法FindFather）

3. 搜索指定数据域的结点

a. 算法FindTarget

b. 算法解析

  算法FindTarget在以t为根指针的树中搜索数据成员等于target的节点，类似先根遍历，其时间复杂度为O(n) 。

1. 首先，将result指针设置为空。
2. 如果t为空，直接返回。
3. 如果t的数据成员等于target，表示找到了目标节点，将result指针指向t，然后返回。
4. 将指针p指向t的第一个子节点。
5. 进入一个循环，只要p不为空：
   • 递归调用FindTarget函数，传入参数p和target，并将结果存储在result中。
   • 如果result不为空，表示已经找到了目标节点，直接返回。
   • 将指针p更新为p的下一个兄弟节点。
6. 如果循环结束仍然没有找到目标节点，那么result仍然为空。

c. 代码实现

a. 使用指向指针的指针

TreeNode* FindTarget(TreeNode* t, char target) {
    if (t == NULL) {
        return NULL;
    }

    if (t->data == target) {
        return t;
    }

    TreeNode* p = t->firstChild;

    while (p != NULL) {
        struct TreeNode* resultt = FindTarget(p, target);

        if (resultt != NULL) {
            return resultt;
        }

        p = p->nextBrother;
    }
}

b. 直接返回找到的节点

void FindTarget(TreeNode* t, char target, TreeNode** result) {
    *result = NULL;

    if (t == NULL) {
        return;
    }

    if (t->data == target) {
        *result = t;
        return;
    }

    TreeNode* p = t->firstChild;

    while (p != NULL) {
        FindTarget(p, target, result);

        if (*result != NULL) {
            return;
        }

        p = p->nextBrother;
    }
}

  两种实现方式在逻辑上是等价的，主要的区别在于结果的返回方式和对指针的处理。

4. 代码整合

#include <stdio.h>
#include <stdlib.h>

// 定义树节点
typedef struct TreeNode {
    char data;
    struct TreeNode* firstChild;
    struct TreeNode* nextBrother;
} TreeNode;

// 创建树节点
TreeNode* createNode(char data) {
    TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));
    if (newNode != NULL) {
        newNode->data = data;
        newNode->firstChild = NULL;
        newNode->nextBrother = NULL;
    }
    return newNode;
}

// 释放树节点及其子树
void freeTree(TreeNode* root) {
    if (root != NULL) {
        freeTree(root->firstChild);
        freeTree(root->nextBrother);
        free(root);
    }
}

// 算法GFC：获取大儿子结点
TreeNode* getFirstChild(TreeNode* p) {
    if (p != NULL && p->firstChild != NULL) {
        return p->firstChild;
    }
    return NULL;
}

// 算法GNB：获取下一个兄弟结点
TreeNode* getNextBrother(TreeNode* p) {
    if (p != NULL && p->nextBrother != NULL) {
        return p->nextBrother;
    }
    return NULL;
}


// 队列结构
typedef struct QueueNode {
    TreeNode* treeNode;
    struct QueueNode* next;
} QueueNode;

typedef struct {
    QueueNode* front;
    QueueNode* rear;
} Queue;

// 初始化队列
void initQueue(Queue* q) {
    q->front = NULL;
    q->rear = NULL;
}

// 入队列
void enqueue(Queue* q, TreeNode* treeNode) {
    QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
    newNode->treeNode = treeNode;
    newNode->next = NULL;

    if (q->rear == NULL) {
        q->front = newNode;
        q->rear = newNode;
    } else {
        q->rear->next = newNode;
        q->rear = newNode;
    }
}

// 出队列
TreeNode* dequeue(Queue* q) {
    if (q->front == NULL) {
        return NULL; // 队列为空
    }

    TreeNode* treeNode = q->front->treeNode;
    QueueNode* temp = q->front;

    q->front = q->front->next;
    free(temp);

    if (q->front == NULL) {
        q->rear = NULL; // 队列为空
    }

    return treeNode;
}

// 层次遍历的算法
void LevelOrder(TreeNode* root) {
    if (root == NULL) {
        return;
    }

    Queue queue;
    initQueue(&queue);

    enqueue(&queue, root);

    while (queue.front != NULL) {
        TreeNode* p = dequeue(&queue);

        while (p != NULL) {
            // 访问当前结点
            printf("%c ", p->data);

            // 将大儿子结点入队列
            if (getFirstChild(p) != NULL) {
                enqueue(&queue, getFirstChild(p));
            }

            // 移动到下一个兄弟结点
            p = getNextBrother(p);
        }
    }
}

// 算法 FindTarget
void FindTarget(TreeNode* t, char target, TreeNode** result) {
    *result = NULL;

    if (t == NULL) {
        return;
    }

    if (t->data == target) {
        *result = t;
        return;
    }

    TreeNode* p = t->firstChild;

    while (p != NULL) {
        FindTarget(p, target, result);

        if (*result != NULL) {
            return;
        }

        p = p->nextBrother;
    }
}

// TreeNode* FindTarget(TreeNode* t, char target) {
//     if (t == NULL) {
//         return NULL;
//     }
//
//     if (t->data == target) {
//         return t;
//     }
//
//     TreeNode* p = t->firstChild;
//
//     while (p != NULL) {
//         struct TreeNode* resultt = FindTarget(p, target);
//
//         if (resultt != NULL) {
//             return resultt;
//         }
//
//         p = p->nextBrother;
//     }
// }


int main() {
    // 构建左儿子右兄弟链接结构的树
    TreeNode* A = createNode('A');
    TreeNode* B = createNode('B');
    TreeNode* C = createNode('C');
    TreeNode* D = createNode('D');
    TreeNode* E = createNode('E');
    TreeNode* F = createNode('F');

    A->firstChild = B;
    B->nextBrother = C;
    C->nextBrother = D;
    C->firstChild = E;
    E->nextBrother = F;

    // 要查找的目标值
    char targetValue = 'C';

    // 使用算法 FindTarget 查找结点
    // TreeNode* result = FindTarget(A, targetValue);
    TreeNode* result = NULL;
    FindTarget(A, targetValue, &result);

    // 输出结果
    if (result != NULL) {
        printf("Node with data %c found.\n", targetValue);
    } else {
        printf("Node with data %c not found.\n", targetValue);
    }
    // 层次遍历
    printf("Level Order: \n");
    LevelOrder(result);
    printf("\n");

    // 释放树节点
    freeTree(A);

    return 0;
}