231128 刷题日报
值班+刷题的第二天,早上地铁上看了一道题,以为很简单
LCR 019. 验证回文串 II
我的思路是引入计数器+左右指针,然而
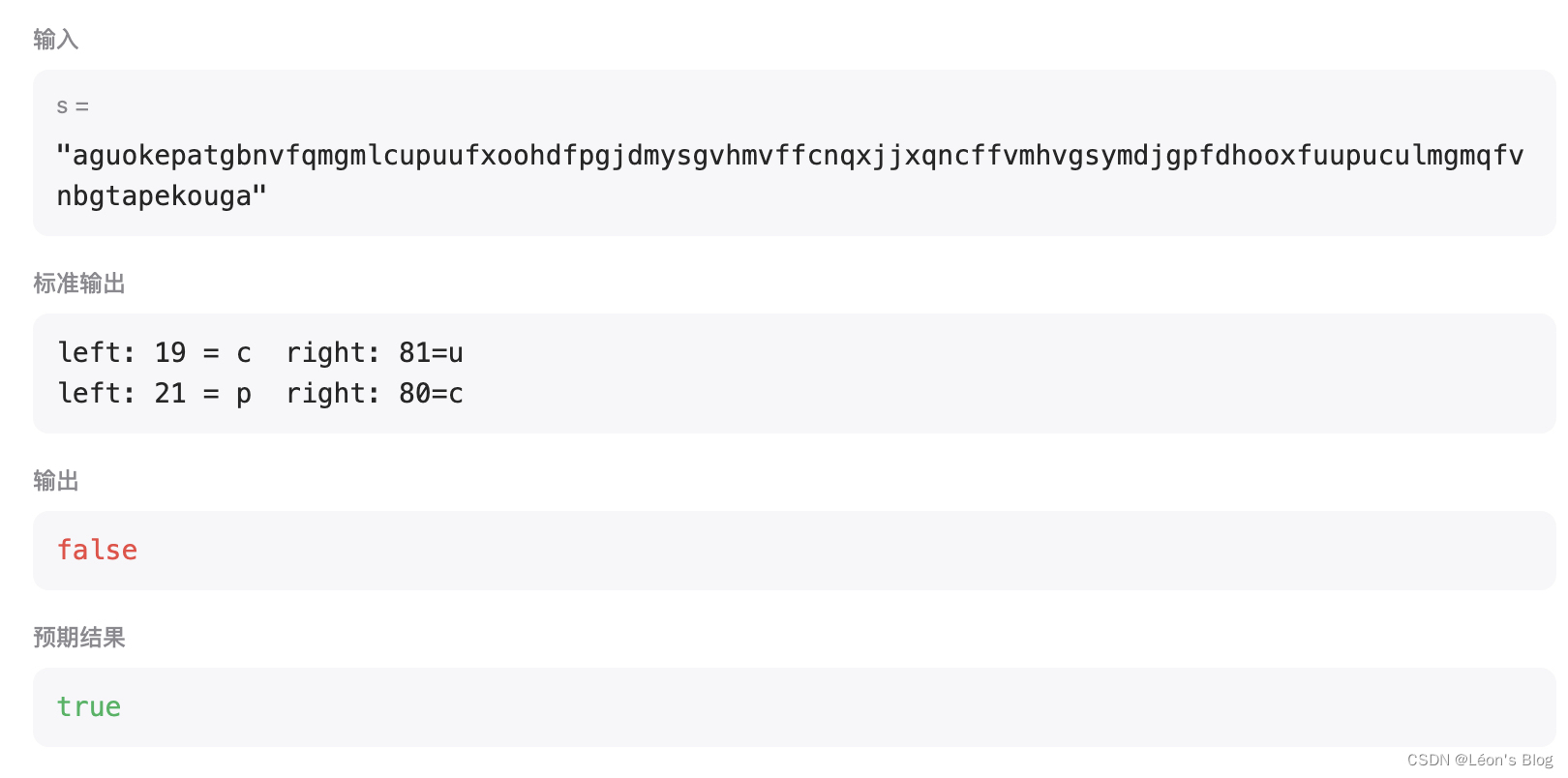
Leetcode老哥提醒了我:
你看看这个字符串“lcuxxucul”,你的默认优先删除左边,但是删除左边是false,如果删除右边就是true
所以这题还是要dp实现的
另外整理下DP
| 0-1背包 | 子集背包 | 完全背包 | |
如果限定每件物品最多只能选取 1次(即 0 或 1次),则问题称为 0-1背包问题 | 如果每件物品最多可以选取无限次,则问题称为完全背包问题 | ||
| dp数组定义 | 对于前i个物品,当前背包容量是w,这种情况下可以装的最大价值是dp[i][w] | dp[i][j] = x表示,对于前i个物品,当前背包容量是j时,若x为true,则说明背包可以恰好装满;若x为false,则说明不能恰好把背包装满。 | dp[i][j]定义如下; 只使用前i种物品,装满背包容量j,有dp[i][j]个方法 从前 i种硬币中组成金额 j所需最少的硬币数量。 |
| 状态转移 | 选:dp[i - 1][w - wt[i-1]] + val[i-1] 不选:dp[i - 1][w] | ||
| 推导式 | dp[i][w] = max(dp[i - 1][w - wt[i-1]] + val[i-1], dp[i - 1][w]); | dp[i][j] = dp[i - 1][j] || dp[i - 1][j-nums[i-1]]; | dp[i][j] = dp[i - 1][j] + dp[i][j-coins[i-1]]; |
| base case | dp[0][..] = 0 dp[..][0] = 0 没有物品或者没有背包空间时,最大价值是0 | dp[0][..] = true dp[..][0] = false 没有物品选择时,肯定没办法装满背包; 背包没有空间时,相当于背包满了。 | dp[0][..] = 0 dp[..][0] = 1 如果不使用任何硬币面值,无法凑出金额; 如果目标金额为0,那么无为而治也是一种凑法。 |
| 应用 | 494. 目标和 416. 分割等和子集 474. 一和零 1049. 最后一块石头的重量 II | 322. 零钱兑换 剑指 Offer II 103. 最少的硬币数目 518. 零钱兑换 II 279. 完全平方数 |
求最优解的背包问题中,有的题目要求恰好装满背包时的最优解,有的题目则要求不超过背包容量时的最优解。一种区别这两种问法的实现方法是在状态初始化的时候有所不同
两种问法的实现方法是在状态初始化的时候有所不同。
初始化的 dpdpdp 数组事实上就是在背包中没有放入任何物品时的合法状态:
如果要求恰好装满背包,那么在初始化时 dp[i][0]=0,其它 dp[i][1,2,...,∗] 均设为 −∞。
这是因为此时只有容量为 0的背包可能被价值为 0 的 nothing “恰好装满”,而其它容量的背包均没有合法的解,属于未定义的状态。
如果只是要求不超过背包容量而使得背包中的物品价值尽量大,初始化时应将 dp[∗][∗]全部设为 0。
这是因为对应于任何一个背包,都有一个合法解为 “什么都不装”,价值为 000。
