MATLAB-Lingo求解线性规划问题-奶制品2
奶制品的生产销售计划,给定条件不变
为了增加工厂的获利,开发了奶制品的深加工技术:用2小时和3元加工费,可将1kgA1加工成0.8kg高级奶制品B1,也可将1kgA2加工成0.75kg高级奶制品B2,每千克B1能获利44元,每千克B2能获利32元.试为该厂制定一个生产计划,使每天获利最大,进一步讨论以下2个附加问题:
- 如果投资30元可以增加供应1桶牛奶,投资3元可增加1h劳动时间,是否应作这项投资?如果每天投资150元,可赚回多少?
- 每千克高级奶制品B1,B2的获利经常有10%的波动,对制定的生产销售计划有无影响,如果每千克B1获利下降10%,计划应该变化吗?
解:
设生产 x1 千克 A1,x2千克A2, x3千克B1, x4千克 B2,x5千克 A1加工B1,x6千克A2加工B2。
目标函数:
原料供应
劳动时间
加工能力
附加约束
非负约束
Max=24*x1+16*x2+44*x3+32*x4-3*x5-3*x6;
4*x1+3*x2+4*x5+3*x6<=600;
4*x1+2*x2+6*x5+4*x6<=480;
x1+x5<=100;
x3=0.8*x5;
x4=0.75*x6;
每天销售168千克A2,19.2千克B1,24千克A1加工成B1,可使每天获利最大,利润为3460.8元
(1)增加1桶牛奶可使利润增加3.16×12=37.92元,增加1小时劳动时间可增加利润3.26元,所以应作这项投资。
如果每天投资150元,增加5桶牛奶,可赚5×37.92=189.6元;增加50小时劳动时间,可赚163元,故应增加牛奶。
作灵敏度分析
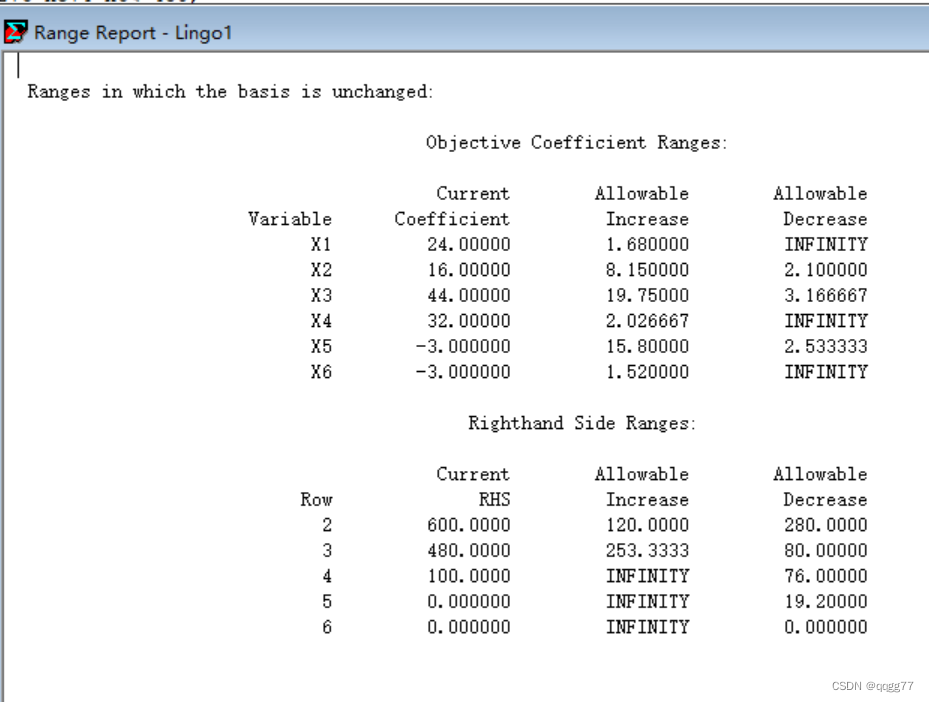
B1获利下降10%,超出X3系数允许范围
B2获利上升20%,超出X4系数允许范围
故波动对计划有影响。
生产计划应重新制定,比如将x3的系数改为44(1-10%)=39.6计算,会发现结果会有很大变化。
