当前位置： 首页 > article >正文

深度学习记录--logistic回归损失函数向量化实现

article 2024/11/16 3:22:10

前言

再次明确向量化的目的：减少for循环的使用，以更少的代码量和更快的速度来实现程序

正向传播的向量化

对于z^{i}=w^{T}x^{i}+b,i=1,2,...,m,用向量化来实现，只需要Z=np.dot(w.T,X)+b就可以完成，其中Z=\begin{bmatrix} z^{1}&z^{2}&...&z^{m} \end{bmatrix},w=\begin{bmatrix} w^{1} &w^{2} &... &w^{m} \end{bmatrix},X=\begin{bmatrix} | &| & | & |\\ x^{1}& x^{2} & ...&x{m} \\ |& | & | &| \end{bmatrix}

ps.这里b只是一个常数，但是依然可以加在每个向量里(python的广播(Broadcasting))

激活函数a^{i}=\sigma (z^{i}),i=1,2,...,m,同样用向量化实现，只需要A=\sigma (Z)就可以完成，其中A=\begin{bmatrix} a^{1} & a^{2} &... &a^{m} \end{bmatrix}

因此，正向传播的向量化，我们只用了两行代码就完成了

反向传播的向量化

与正向传播的向量化实现类似，也是用矩阵来计算

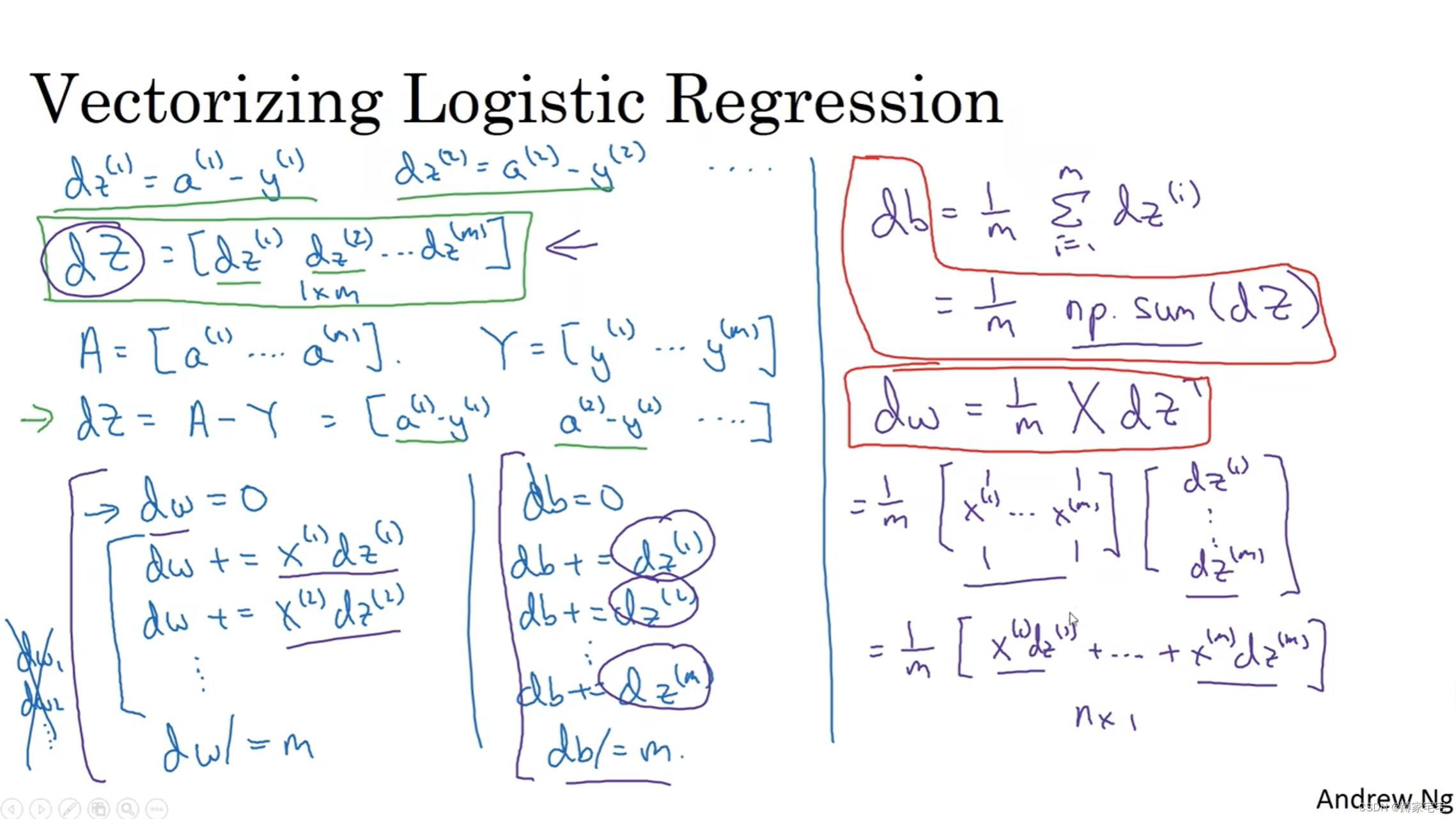
最后对w和b进行更新即可

当然，进行多次样本的训练还是要用for循环来实现，但是速度已经提升很多了


http://www.kler.cn/a/155017.html

相关文章：

  • 【Qt聊天室客户端】消息功能--发布程序
  • SpringCloud 微服务消息队列灰度方案 (RocketMQ 4.x)
  • 解读Nature：Larger and more instructable language models become less reliable
  • STM32 51单片机设计半导体制冷片温控设计
  • Python 中.title()函数和.lower()函数
  • python——面向对象
  • LLM；超越记忆《第 2 部分 》
  • Echarts地图registerMap使用的GeoJson数据获取
  • Spring boot命令执行 (CVE-2022-22947)漏洞复现和相关利用工具
  • 高斯日记(cpp+java)
  • 线程安全的问题以及解决方案
  • 【重点】【双指针】15. 三数之和
  • Vue diff 算法探秘：如何实现快速渲染
  • Gson的用法详解
  • 中兴小鲜50 ZTE 畅行50 刷机救砖演示机7543n root 虎贲 展锐 T760 解锁BL
  • 人工智能 - 人脸识别：发展历史、技术全解与实战
  • 开源免费跨平台数据同步工具-Syncthing
  • Unity3D URP 自定义范围的特效热扭曲详解
  • LLM:《第 3 部分》从数学角度评估封闭式LLM的泛化能力
  • 安全SCDN对网站蜘蛛抓取有影响吗，使用SCDN对百度蜘蛛抓取有否好处
  • CentOS7 网络配置
  • Linux的权限（一）
  • Ubuntu22.04无需命令行安装中文输入法
  • C++生成静态库和动态库
  • 智慧用电安全动态监控系统
  • centos7-docker安装与使用