循环队列中的求队列长度公式怎么来的?【数学角度】
循环队列中的队列长度怎么来的?
引入
在一个循环队列中,队列的元素个数可以通过头指针(Front,通常用F表示)和尾指针(Rear,通常用R表示)来计算。假设队列的存储空间大小为n,队列中元素的个数(即队列长度)可以通过以下公式计算:
队列长度 = (R−F+n)%n
这个公式的含义是:尾指针R减去头指针F,加上n再取模n。这是因为R - F可能为负数,通过加上n保证结果始终为正数,然后再对n取模,确保结果在队列容量范围内。
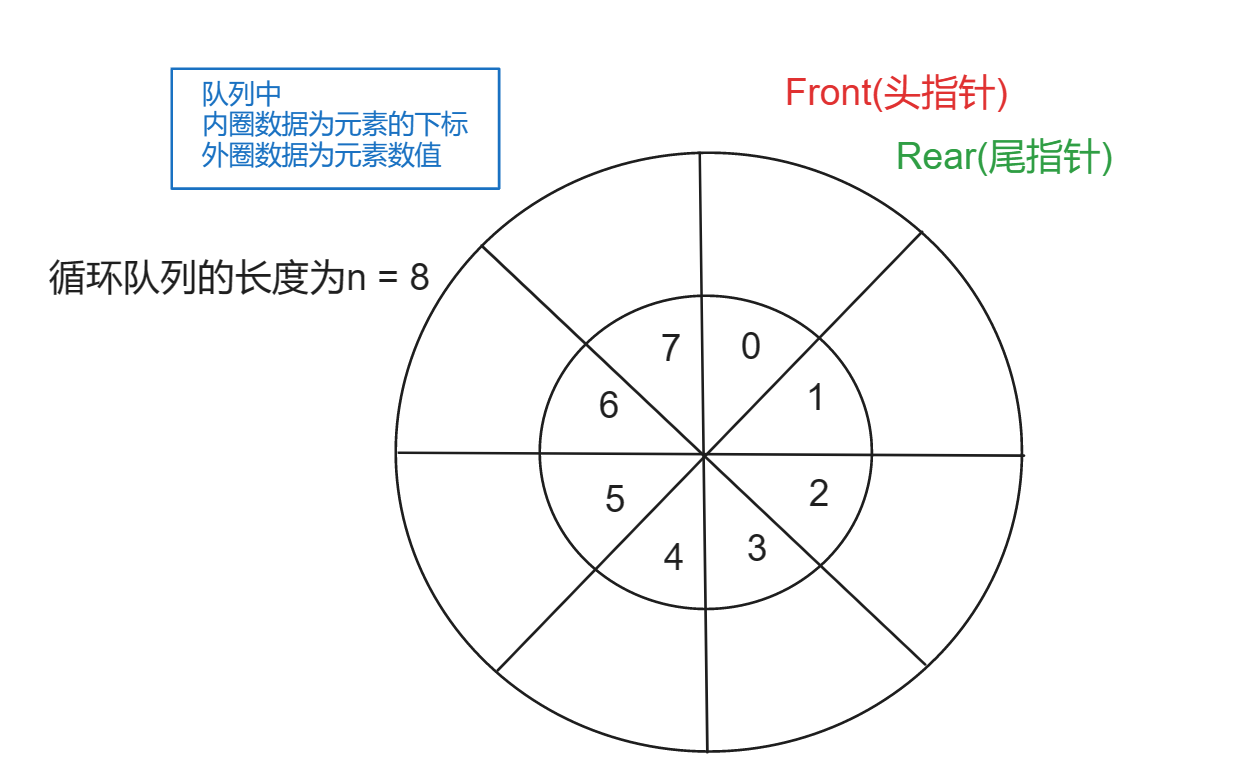
例题 + 图示
- 情况1 R > F
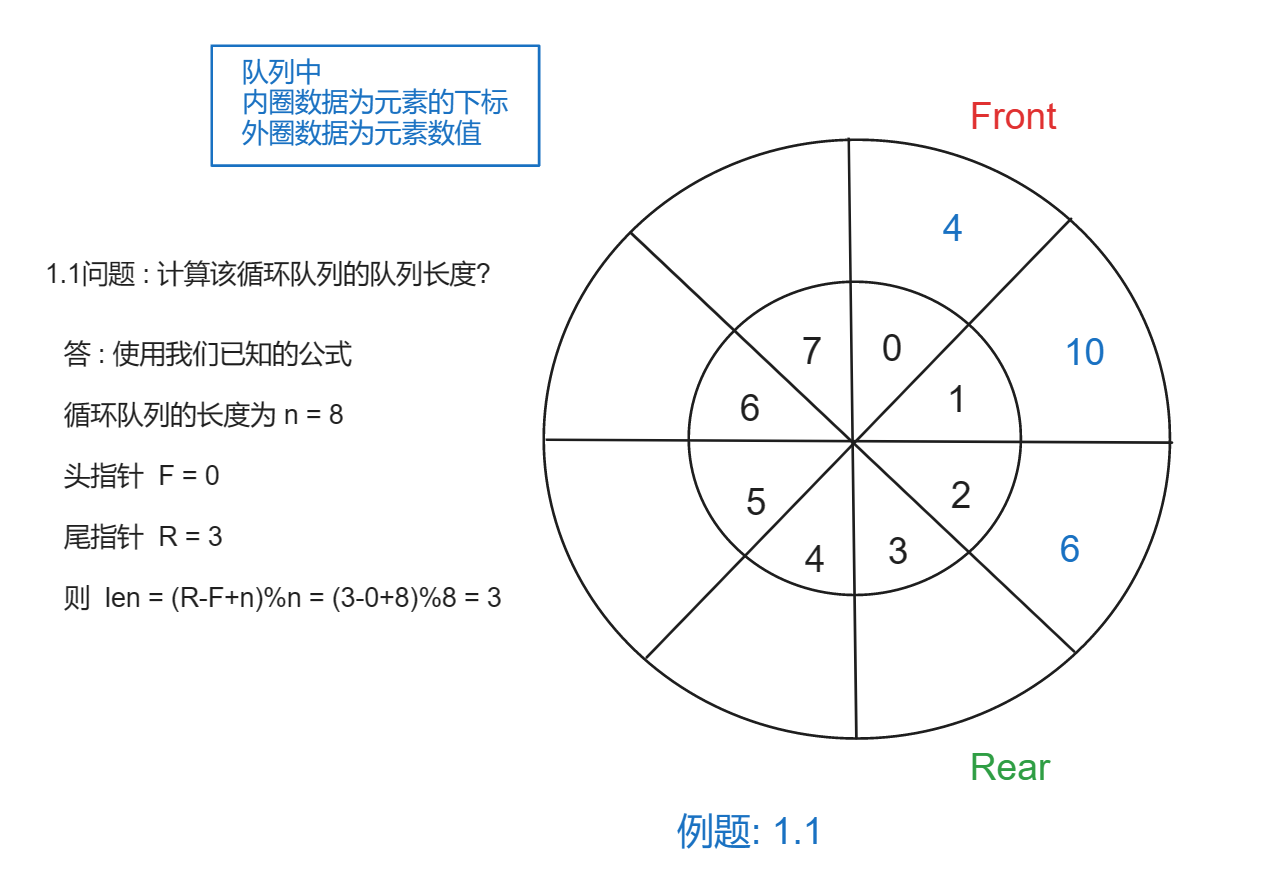
- 情况2 R < F
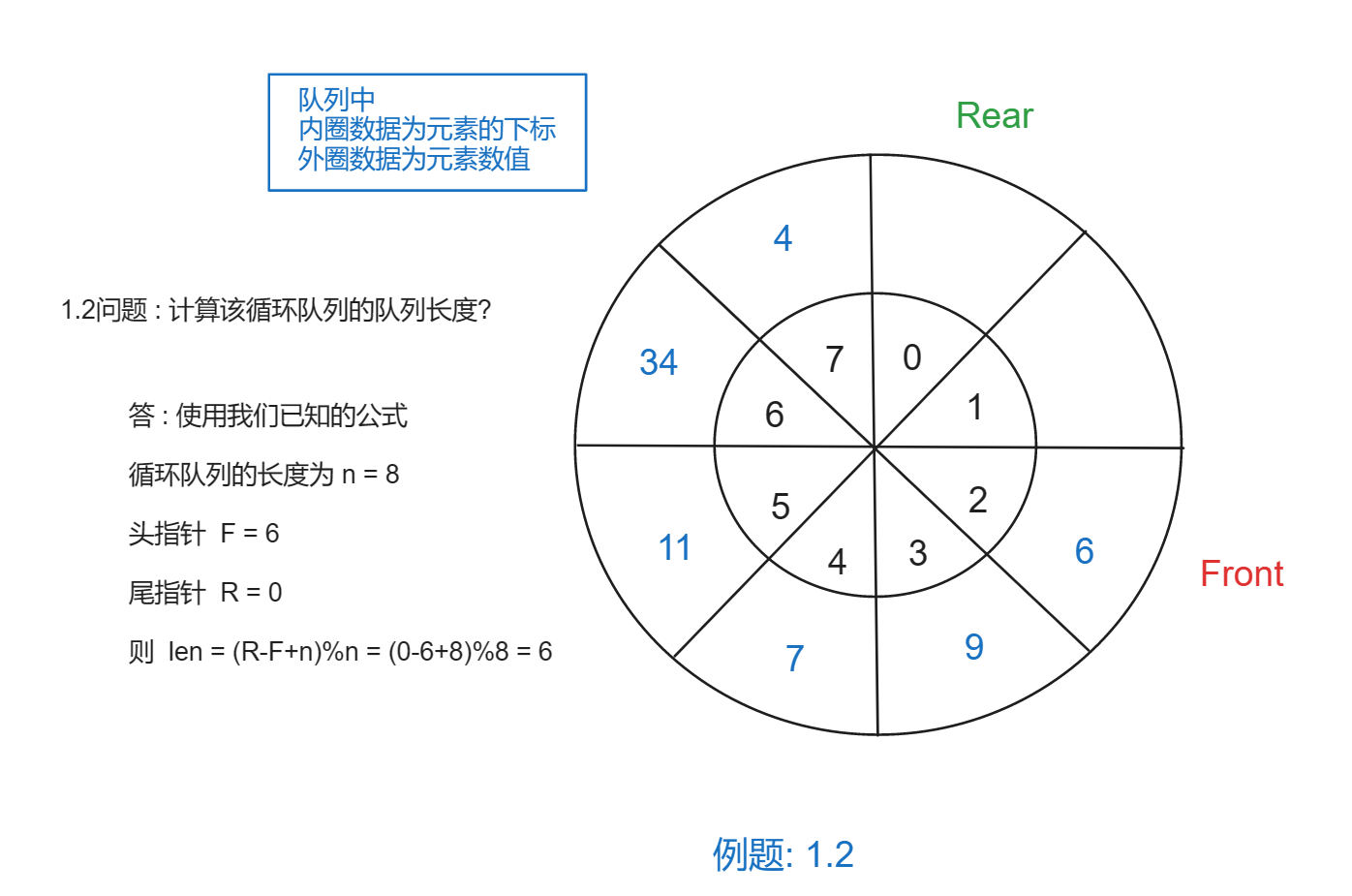
上述我们已经会使用循环队列求队列的公式了,那么这个公式是如何来的呢 ?
知其然,亦知其所以然
数学角度理解
从数学的角度来理解循环队列中队列长度的计算涉及到模运算(余数运算)的概念。首先,我们先了解一下模运算的定义:
给定整数a和正整数n,a mod n的值就是a除以n的余数。这可以表示为:
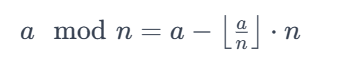
这样的定义保证了 0 ≤ a mod n < n
在循环队列中,头指针F和尾指针R的差值(R - F)可以表示队列的长度。然而,由于队列是循环的,当尾指针R超过了队列的最大容量n时,尾指针需要回到队列的开头,即回到0的位置。这时候 R−F 就可能变成负数。也就是我上述列举的例题 1.2 的情况, R-F < 0
为了得到正确的队列长度,我们使用模运算。具体来说,我们加上n,这样就将负数变成了正数,然后再取模n,确保结果在合法范围内。这就是为什么队列长度的计算公式是 (R−F+n)%n 的原因。
总结
通过这种方式,我们能够正确地计算出循环队列中的队列长度,考虑了队列循环的特殊性。这种数学定义和计算方式有助于在实际编程中处理循环队列时保持正确性。

