【华为OD题库-043】二维伞的雨滴效应-java
题目
普通的伞在二维平面世界中,左右两侧均有一条边,而两侧伞边最下面各有一个伞坠子,雨滴落到伞面,逐步流到伞坠处,会将伞坠的信息携带并落到地面,随着日积月累,地面会呈现伞坠的信息。
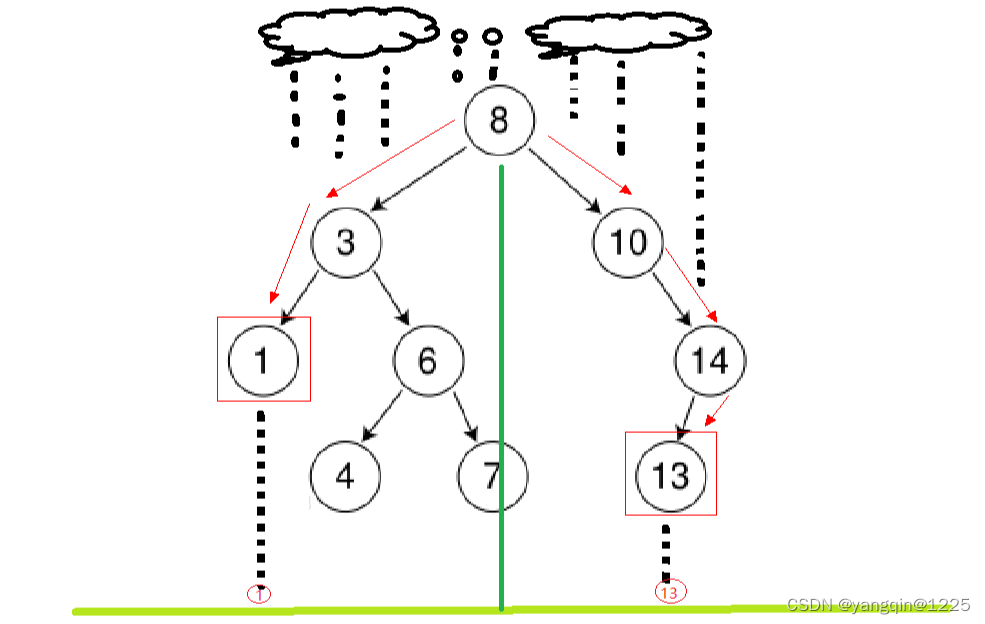
1、为了模拟伞状雨滴效应,用二叉树来模拟二维平面伞(如下图所示),现在输入一串正整数数组序列(不含0,数组成员至少是1个),若此数组序列是二叉搜索树的前序遍历的结果,那么请输出一个返回值1,否则输出0.
2、同时请将此序列构成的伞状效应携带到地面的数字信息输出来(左边伞坠信息,右边伞坠信息,详细参考示例图地面上数字),若此树不存在左或右扇坠,则对应位置返回0。同时若非二叉排序树那么左右伞坠信息也返回0.
输入描述:
1个通过空格分割的整数序列字符串,数组不含0,数组成员至少1个,输入的数组的任意两个数字都互不相同,最多1000个正整数,正整数值范围1~65535
输出描述:
输出如下三个值,以空格分隔:是否二叉排序树,左侧地面呈现的伞坠数字值,右侧地面呈现的伞坠数字值.若是二叉排序树,则输出1,否则输出0(其左右伞坠值也直接赋值0)。
若不存存在左侧或者右侧伞坠值,那么对应伞坠值直接赋值0。
示例1
输入:
8 3 1 6 4 7 10 14 13
输出:
1 1 13
说明:
1 表示是二叉搜索树前序遍历结果,1表示左侧地面呈现的伞坠数字值,13表示右侧地面呈现的伞坠数字值
思路
同leetcode:1008. 前序遍历构造二叉搜索树
本题化解为两个问题
- 根据前序遍历数组(中>左>右),判断其是否能构成二叉搜索树(左节点<中间节点<右节点)
以示例数据为例:8 3 1 6 4 7 10 14 13
根据前序遍历及二叉搜索树的特点,第一个数8应该为根节点,其后面小于8的所有数(3 1 6 4 7)在8的左边,大于8的所有数(10 14 13 )在8的右边。问题化解为两个字数组是否为二叉搜索树,用同样的办法递归判断即可。
- 设计dfs方法为:dfs(nums,start,end),当前节点为nums[start],设i=start+1,不断右移i,先找到第一个比当前节点大的数在索引,【start+1,i-1】就是左节点的部分;
- 继续右移i,直到i越界或者nums[i]小于当前值。
- 如果最后i是越界的(i=end+1),说明后面的数都比nums[start]大,满足二叉搜索树的规律,继续递归两个子数组;【start+1,i-1】和【i,end】;递归中止条件是start==end,即只有一个数字,返回true
- 否则,不满足,直接返回false
- 求左右伞坠,关键在于理解左右伞坠的定义,题目并没有明确说明,我的理解如下:
- 如果不是二叉搜索树,左右伞坠直接置0
- 如果根节点没有左子树,那么左伞坠为0,如果没有右子树,那么右伞坠为0
- 寻找左伞坠的方法,优先寻找左子树,当左节点为空时,再找右节点
- 寻找右伞坠的方法,优先寻找右子树,当右节点为空时,再找左节点
比如示例数据:8 3 1 6 4 7 10 14 13,输出1 1 13
删除一个节点:8 3 6 4 7 10 14 13,输出1 4 13
只要左子树:8 3 1 6 4 7,输出:1 1 0
只要右子树:8 10 14 13,输出:1 0 13
只要根节点:8,输出:1 0 0
题解
package hwod;
import java.util.Arrays;
import java.util.Scanner;
public class UmbrellaRainDrop {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int[] nums = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
int[] res = umbrellaRainDrop(nums);
for (int i = 0; i < res.length; i++) {
if (i != 0) System.out.print(" ");
System.out.print(res[i]);
}
System.out.println();
}
private static int[] umbrellaRainDrop(int[] nums) {
boolean isSearchTree = recur(nums, 0, nums.length - 1);
if (!isSearchTree) return new int[]{0, 0, 0};
int leftNum = findLastNum(nums, 0, nums.length - 1, true);
int rightNum = findLastNum(nums, 0, nums.length - 1, false);
return new int[]{1, leftNum, rightNum};
}
private static int findLastNum(int[] nums, int start, int end, boolean isLeft) {
if (start == end) return start == 0 ? 0 : nums[start];
int i = start + 1;
while (i <= end && nums[i] < nums[start]) i++;
//处理没有左右伞坠的情况
if (isLeft && i == start + 1 && start == 0) return 0;
if (!isLeft && i == end + 1 && start == 0) return 0;
if (isLeft) {
//先找左边,如果没有左节点,就找右节点
return i == start + 1 ? findLastNum(nums, i, end, isLeft) : findLastNum(nums, start + 1, i - 1, isLeft);
} else {
//先找右边,如果没有右节点,就找左节点
return i == end + 1 ? findLastNum(nums, start + 1, i - 1, isLeft) : findLastNum(nums, i, end, isLeft);
}
}
private static boolean recur(int[] nums, int start, int end) {
if (start > end) {
return true;
}
int i = start + 1;
while (i <= end && nums[i] < nums[start]) i++;
int tmp = i;
while (i <= end && nums[i] > nums[start]) i++;
if (i != end + 1) return false;
return recur(nums, start + 1, tmp - 1) && recur(nums, tmp, end);
}
}
推荐
如果你对本系列的其他题目感兴趣,可以参考华为OD机试真题及题解(JAVA),查看当前专栏更新的所有题目。