C++ 红黑树的封装
一.map/set的封装
在实现了红黑树的部分功能后,我们可以便可以将红黑树作为底层结构来封装map 和 set ,但是问题也随之而来。我们都知道map是k-v的数据模型,而set是k的数据模型,我们难道要去使用两棵红黑树来封装吗?显然不是这样的。
接下来我们将使用同一棵红黑树实现 map和set。
1.1 封装的基本思路
因为我们是用一棵红黑树去封装两种容器,使用我们的这棵红黑树,使用我们的这棵树就不能像以前一样写死成k-v模型的数据结构,需要稍作修改。
因为红黑树不能自己判断其是否是map/set类型,我们能做的努力就是提高其适应性,对红黑树的要求为:
既能适配 K-V模型的map,又能适配出K 模型的set。
对map和set的要求为:
需要准确的传入数据,传入时让红黑树只能适配出一个类型的容器,对不需要的部分进行切割。
1.2 红黑树节点的调整
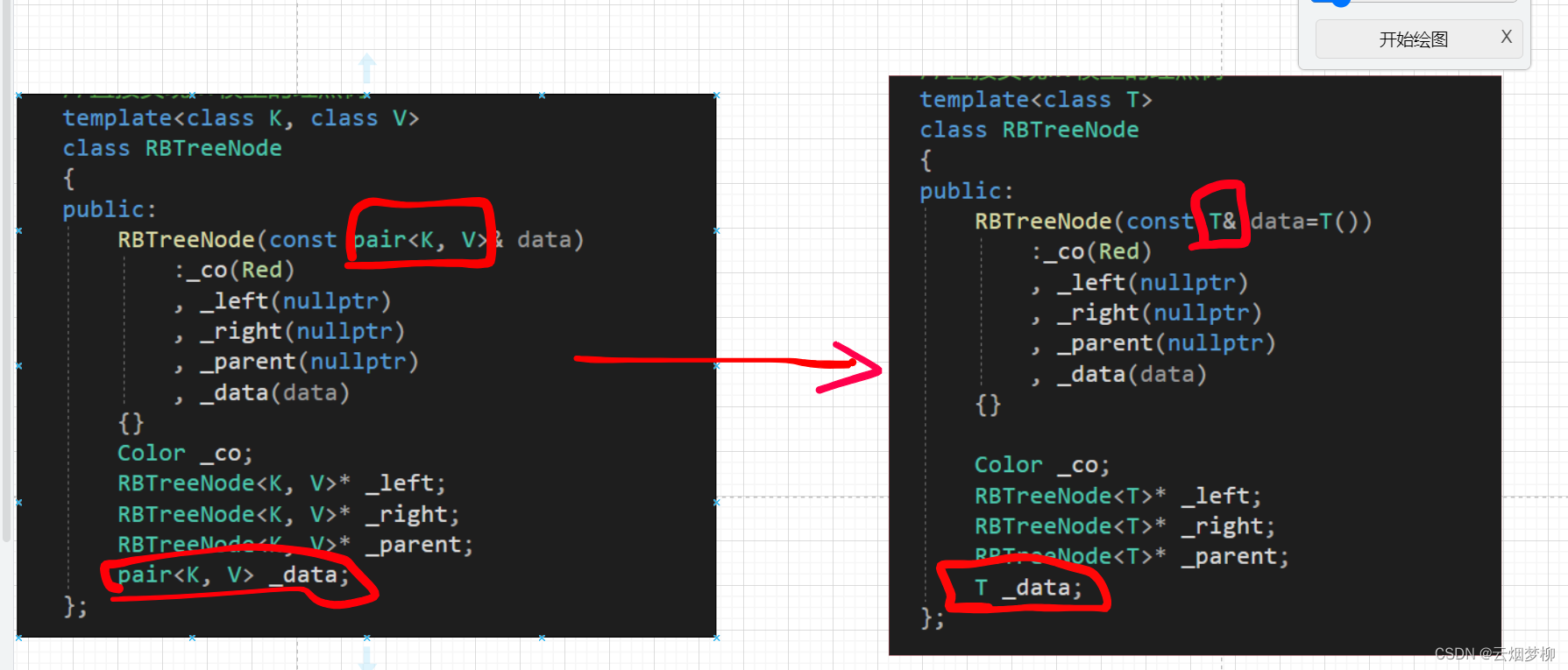
这是我们之前写出的红黑树节点,现在来看显然不太合适,因为我们已经把K-V模型写死了,不太好适配出K模型的set。
在这里,我们建议让pair类型变成 一个模糊的 T类型,至于是pair 类型还是 k类型,我们希望让map和set来准确的传入。
1.3 map 和 set 的定义
我们该如何适配map和set的底层,来让其匹配红黑树呢?
在这里,我建议让其内部的模板,暂时先有两个数据类型,第一个为 K 模型,第二个为 T模型,也就是说 当为map时,传入map<K,K>时,底层实际传入RBTree<k,pair<k,k>>,传入set<k>时,底层实际传入RBTree<K,K>。
这样有什么好处呢?
为因为我们的底层实现是红黑树,那么我们为了适应map又适应set,实际传入的代表数据参数至少得是两个,可能会有些人问:“map可以直接传入pair啊,那么为什么不直接传入一个RBTree<pair<K,V>>呢?。
因为有find的存在,map的find是按照k来进行查找的,如果直接传入pair类型,那么红黑树里面的实际类型只有一个pair,当我们查找时,根本无法按照key类型来查找,所以我们的红黑树至少得有两个模板参数。
因此,即使set是k模型,但是在这里的底层结构上,我们仍然需要传入两个k类型。
map和set基本定义如下:
#pragma once
#include"RBTree.h"
using namespace MyRBTree;
namespace MySet
{
template<class K>
class Set
{
private:
RBTree<K, K> _set;
};
} #pragma once
#include"RBTree.h"
using namespace MyRBTree;
namespace MyMap
{
template<class K,class V>
class Map
{
private:
RBTree<K, pair<K,V>> _map;
};
}1.4 仿函数 KeyOfValue
在insert中,我们经常会用到data进行一些比较,但是我们现在data的类型不固定,如果是map中的pair类型,我们就应该用其first进行比较,如果是k类型,我们就应该直接比较。
最好的解决办法是,在map和set内部分别定义一个KetOfValue 仿函数,然后将其传入红黑树模板中,因为其传入的内容不同,所以我们用来分别处理不同的数据。
如果是map中的data,因为是kv结构,所以我们取出其data.first;如果是set中的k模型,那么我们直接返回,仿函数定义如下:
#pragma once
#include"RBTree.h"
using namespace MyRBTree;
namespace MyMap
{
template<class K,class V>
class Map
{
public:
struct MapKeyOfvalue
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
private:
RBTree<K, pair<K,V>, MapKeyOfvalue> _map;
};
}#pragma once
#include"RBTree.h"
using namespace MyRBTree;
namespace MySet
{
template<class K>
class Set
{
public:
struct SetKeyOfvalue
{
const K& operator()(const K& key)
{
return key;
}
};
private:
RBTree<K, K, SetKeyOfvalue> _set;
};
} 同时我们因为要多传入一个仿函数,所以我们的模板和map,set内部的红黑树模板参数也要进行修改: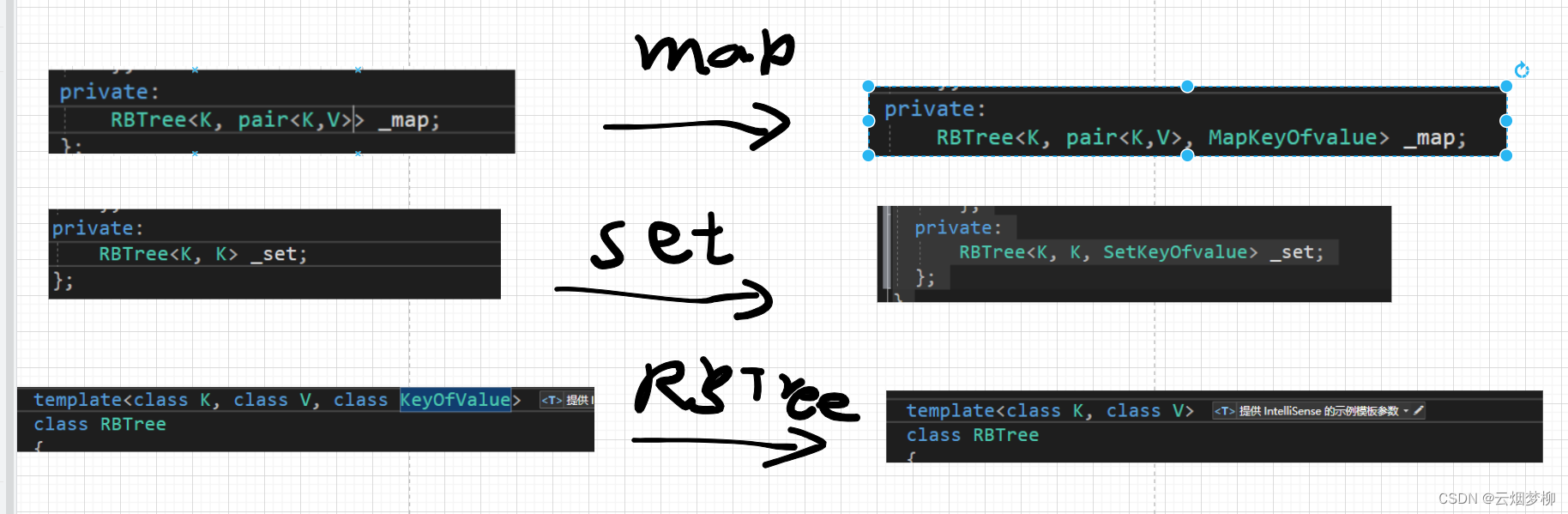
同时,我们在红黑树内部也需要对进行数据比对的函数进行修改,比如说insert和find等等。
bool Insert(const pair<K, V>& data)
{
//因为需要使用仿函数的机会不多,我们在需要用到的地方局部创建一下就可以了
//如何大多数函数都需要用到,建议定义为全局变量
KeyOfValue kot;
if (!_root)
{
_root = new Node(data);
_root->_co = Black;
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
//if (cur->_data.first < data.first)
if (kot(cur->_data)< kot(data))
{
parent = cur;
cur = cur->_right;
}
//else if (cur->_data.first > data.first)
else if (kot(cur->_data) > kot(data.first))
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(data);
cur->_co = Red;
//if (parent->_data.first < cur->_data.first)
if (kot(parent->_data) < kot(cur->_data))
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//开始判断是否需要变色
while (parent && parent->_co == Red)
{
Node* grand = parent->_parent;
if (parent == grand->_left)
{
Node* uncle = grand->_right;
if (uncle && uncle->_co == Red)
{
//这里只变色就好
parent->_co = uncle->_co = Black;
grand->_co = Red;
cur = grand;
parent = cur->_parent;
}
else
{
if (cur == parent->_left)
{
_RotateR(grand);
grand->_co = Red;
parent->_co = Black;
}
else
{
_RotateL(parent);
_RotateR(grand);
cur->_co = Black;
grand->_co = Red;
}
break;
}
}
else
{
Node* uncle = grand->_left;
if (uncle && uncle->_co == Red)
{
//这里只变色就好
parent->_co = uncle->_co = Black;
grand->_co = Red;
cur = grand;
parent = cur->_parent;
}
else
{
if (cur == parent->_right)
{
_RotateL(grand);
grand->_co = Red;
parent->_co = Black;
}
else
{
_RotateR(parent);
_RotateL(grand);
cur->_co = Black;
grand->_co = Red;
}
break;
}
}
}
_root->_co = Black;
return true;
} Node* Find(const K& key)
{
KeyOfValue kot;
Node* cur = _root;
while (cur)
{
//if (cur->_data.first < key)
if (kot(cur->_data) < key)
{
cur = cur->_right;
}
//else if (cur->_data.first > key)
else if (kot(cur->_data) > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}1.5 map/set的插入
现在,在其内部直接套用红黑树的插入即可。
namespace MySet
{
template<class K>
class Set
{
public:
struct SetKeyOfvalue
{
const K& operator()(const K& key)
{
return key;
}
};
bool insert(const K& k)
{
return _set.Insert(k);
}
private:
RBTree<K, K, SetKeyOfvalue> _set;
};
} namespace MyMap
{
template<class K,class V>
class Map
{
public:
struct MapKeyOfvalue
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
bool insert(const pair<K,V> &kv)
{
return _map.Insert(kv);
}
private:
RBTree<K, pair<K,V>, MapKeyOfvalue> _map;
};
}在map和set中先插入一些数据来看一下有没有更改错误:
这里建议在map和set内部封装进去红黑树的Inorder打印一下检查一下错误。
void Inorder()
{
_map.Inorder();
}
//判断一下是否平衡
void IsBalance()
{
_map.IsBalance();
}同时我们的Inorder函数也需要更改
void _Inorder(Node* root)
{
if (!root)
{
return;
}
//这里我们也要更改一下
_Inorder(root->_left);
//cout << root->_data.first << ":" << endl;
cout <<kot(root->_data) <<" ";
_Inorder(root->_right);
}验证一下map和set的准确性:
#include"MyMap.h"
#include"MySet.h"
void testmap()
{
MyMap::Map<int, int> _m;
_m.insert(make_pair(1, 1));
_m.insert(make_pair(2, 1));
_m.insert(make_pair(3, 1));
_m.insert(make_pair(4, 1));
_m.insert(make_pair(5, 1));
_m.Inorder();
_m.IsBalance();
cout << endl << endl;
}
void testset()
{
MySet::Set<int> _s;
_s.insert(1);
_s.insert(2);
_s.insert(3);
_s.insert(4);
_s.insert(5);
_s.Inorder();
_s.IsBalance();
cout << endl<<endl;
}
int main()
{
testmap();
testset();
return 0;
}结果为: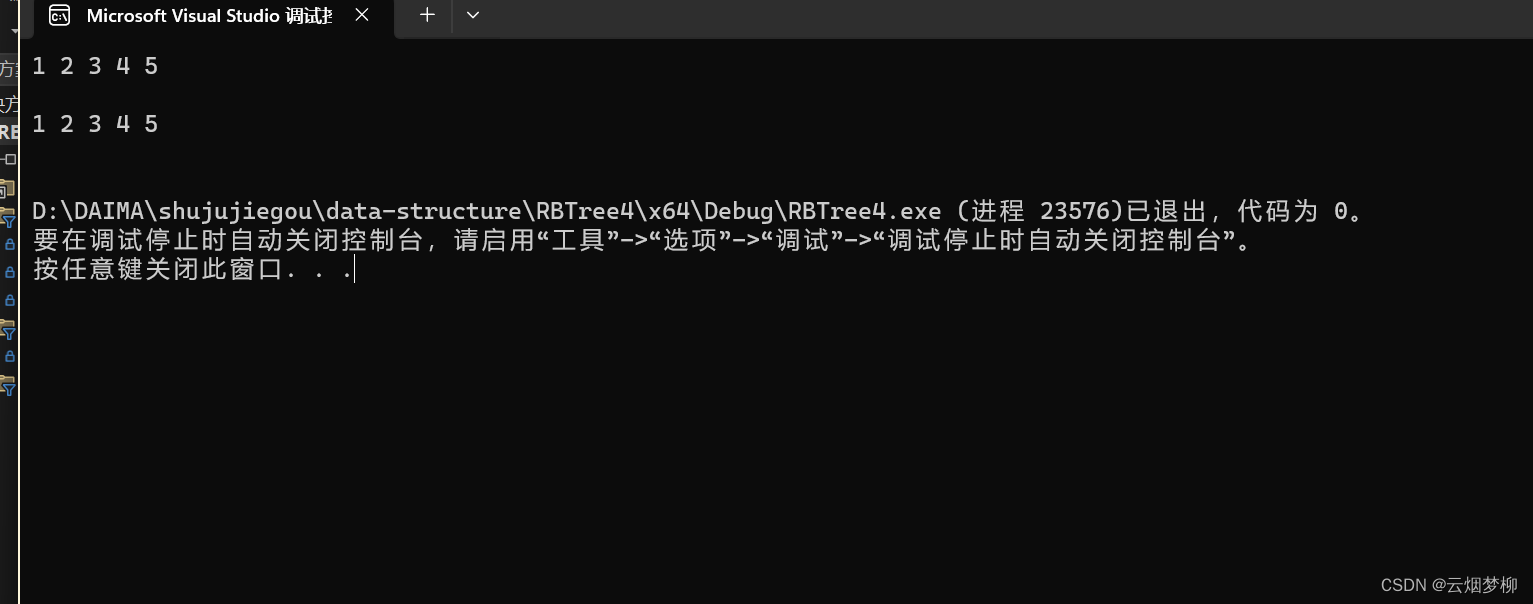
二. map和set迭代器的实现
首先,我们要明白,map/set只是相当于一层壳子,真正的底层实现永远都在红黑树的部分,迭代器也是同理,我们撰写的迭代器应该书写在红黑树部分。
迭代器的基本定义:
// 节点数据 引用/const引用 指针/const指针
template <class T, class Ref, class Ptr>
struct _RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef _RBTreeIterator<T, Ref, Ptr> self;
Node* _node;
_RBTreeIterator(Node* node)
:_node(node)
{}
};2.1 解引用运算符重载
一般用来取出其节点中存储的数据,直接返回data即可,并且一般而言是是可以修改的,因此这里我们返回其引用。
Ref operator*()
{
return _node->_data;
}2.2 成员访问运算符重载
-> 运算符一般用来返回该节点的地址,主要还是适用于map中,用来访问pair里面的first和second成员。
Ptr operator->()
{
return &(_node->_data);
}2.3 == 和 != 运算符重载
这个就比较简单了
bool operator==(const self& s)
{
return _node == s._node;
}
bool operator!=(const self& s)
{
return _node != s._node;
}2.4 begin()和end()
迭代器常用成员函数begin()与end(),其中begin()对应红黑树的最左节点,end()对应最后一个节点的下一个节点,即nullptr(这里我们并没有设置哨兵位,感兴趣的同学可以自己研究一下)
iterator begin()
{
Node* left = _root;
while (left && left->_left)
{
left = left->_left;
}
return iterator(left);
}
iterator end()
{
return iterator(nullptr);
}2.6 ++ 运算符重载
首先我们要知道,红黑树也是一个二叉搜索树,我们对其的遍历顺序也是按照中序遍历,因此,++运算符在这里指的是,中序遍历的下一个节点。
那我们该如何找寻中序遍历的下一个节点呢。
我们先来观察一部分红黑树的遍历情况: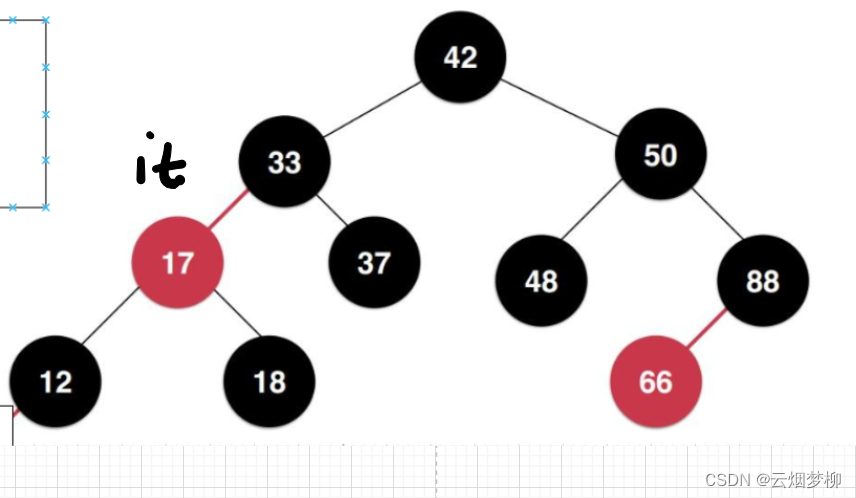
当it指向17 时,++实际上是去访问18这个节点;(17有右子树)
当it访问18时,++实际上是去访问33这个节点;(18无右子树,故向上遍历)
当it访问33时,++实际上是去访问37这个节点;(33有右子树)
当it访问37时,++实际上是去访问42这个节点;(37无右子树,向上遍历)
我们可以看出,实际上++始终围绕着右子树进行移动:
1.当所在节点有右子树时,++访问右子树的最左节点
2.当所在节点没有右子树时,++ 找孩子不是父亲右节点的祖先(这里需要进行遍历)
故得到代码:
self& operator++() //迭代器++,依旧返回迭代器
{
//如果右子树存在
if (_node->_right)
{
Node* left = _node->_right;
//则寻找右子树的最左节点
while (left->_left)
{
left = left->_left;
}
_node = left;
}
//如果右子树不存在
else
{
//找孩子不是父亲右节点的节点
Node* parent = _node->_parent;
Node* cur = _node;
//一定要先判断parent是否存在,以此来避免越界
while (parent&&cur == parent->_right)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
//迭代器后置++
self operator++(int)
{
self it(_node);
++(*this);
return it;
}
2.7 --运算符重载
--就是++ 代码思路反过来。
- 左子树不为空,进行 -- 则是指向左子树(最右节点)。
- 左子树为空,-- 找孩子不是父亲左节点的祖先(循环查找)
得到代码如下:
self& operator--()
{
//如果左子树存在
if (_node->left)
{
//找左子树的最右节点
Node* right = _node->_left;
while (right->_right)
{
right = right->_right;
}
_node = rihgt;
}
//如果左子树不存在
else
{
//找孩子不是父亲左节点的节点
Node* parent = _node->parent;
Node* cur = _node;
while (parent&&parent->_left == cur)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
//后置--
self operator--(int)
{
self it(_node);
--(*this);
return it;
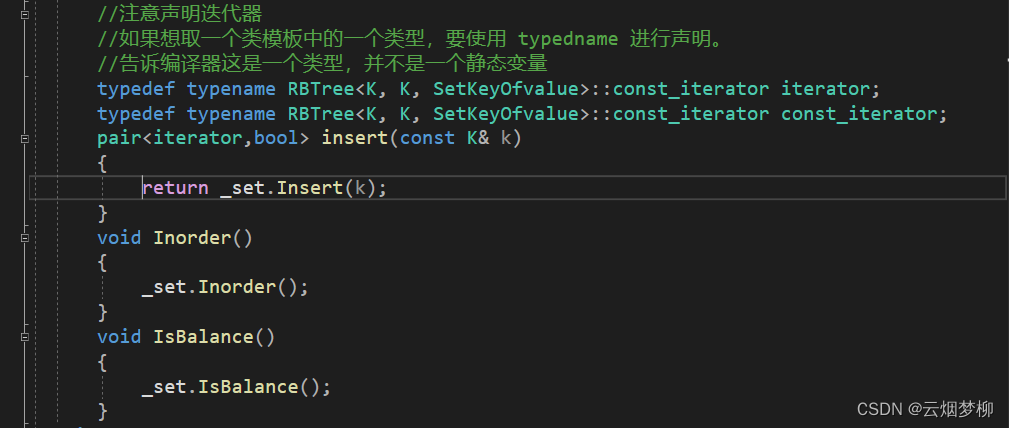
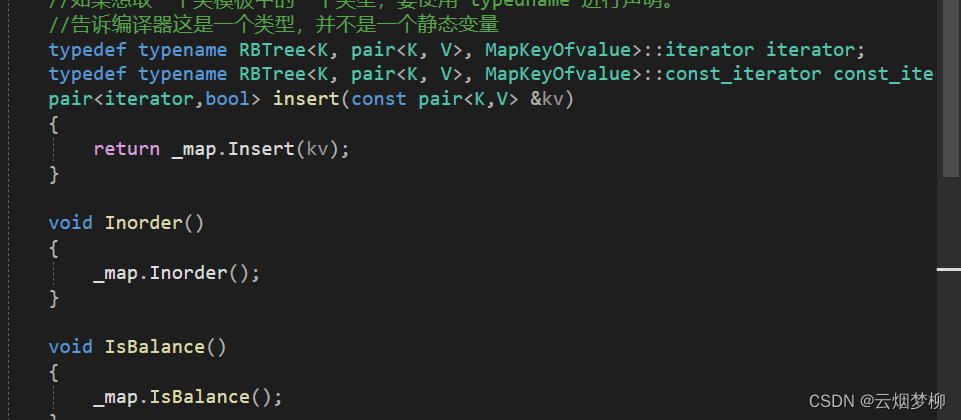
}迭代器在map和set中的封装如下:
三 map的[] 下标访问运算符重载
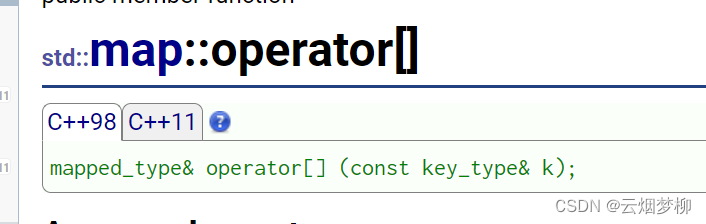
我们可以看到其返回为,mapped_type类型,这是什么呢?
map文档中有如下声明:
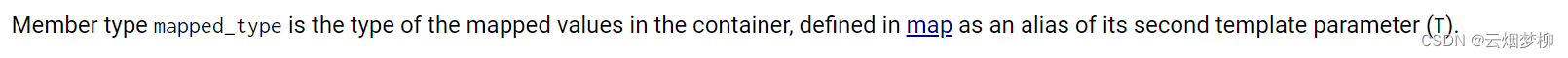
翻译一下我们得知,在map中定义为其第二个模板参数T,(我们这里为V)的别名
在官方库里面,对这个【】是这样实现的:
 太迷茫了,我们拆解来看一下:
太迷茫了,我们拆解来看一下:
里面的第一层为: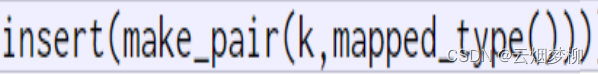
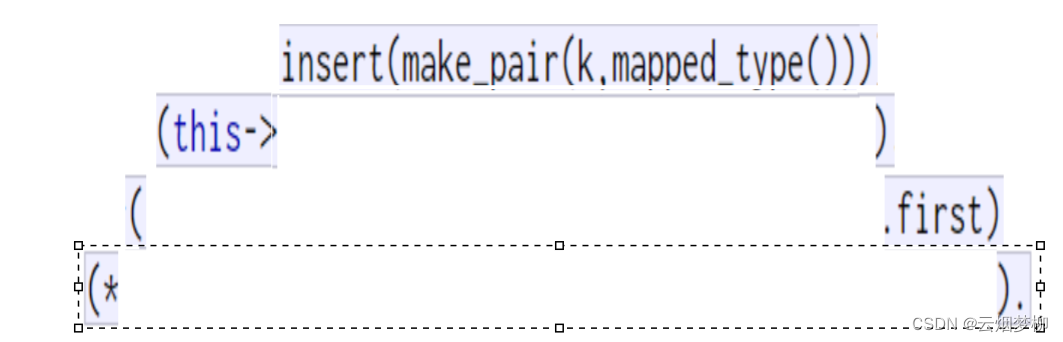
可见就是一层简单的插入 ,第一个传入的是k的值,第二个是我们map中第二个模板参数V的默认构造。
第二步,将this指针指向insert返回的这个内容。
第三步, 取出this指向的内容中的first内容,那么问题来了,我们自己定义的insert返回的内容是bool类型,我们该取这个的first吗,显然不是的,让我们看看库中的insert函数。
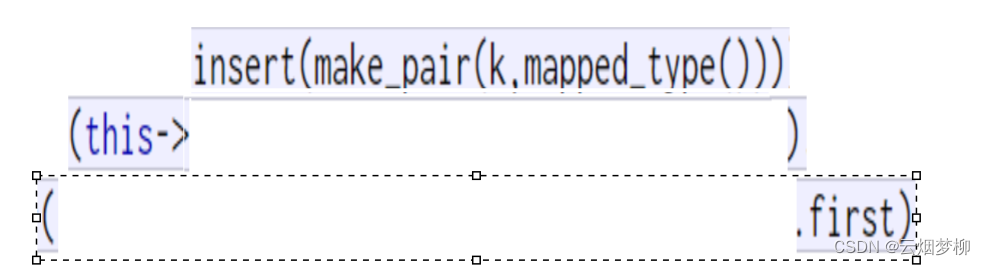
库中的返回值是一个pair类型,其内部分别是一个i迭代器和bool类型,那么这样的作法我们也就理解了,现在我们要修改一下insert。
set中虽然用不到【】但其内部和set是一样定义的。

更改结果如下(RBTree内)
typedef _RBTreeIterator<T, T&, T*> iterator;
typedef _RBTreeIterator<T, const T&, const T*> const_iterator;
iterator begin()
{
Node* left = _root;
while (left && left->_left)
{
left = left->_left;
}
return iterator(left);
}
iterator end()
{
return iterator(nullptr);
}
//bool Insert(const T& data)
pair<iterator, bool> Insert(const T& data)
{
if (!_root)
{
_root = new Node(data);
_root->_co = Black;
//如果成功,返回成功节点的迭代器和true
return make_pair(iterator(_root), true);
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
//if (cur->_data.first < data.first)
if (kot(cur->_data)< kot(data))
{
parent = cur;
cur = cur->_right;
}
//else if (cur->_data.first > data.first)
else if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else
{
//return false;
return make_pair(iterator(cur), false);
}
}
cur = new Node(data);
cur->_co = Red;
//注意这里cur可能因为旋转,改变了原来的位置,所以需要提前记录一下
Node* newnode = cur;
//if (parent->_data.first < cur->_data.first)
if (kot(parent->_data) < kot(cur->_data))
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//开始判断是否需要变色
while (parent && parent->_co == Red)
{
Node* grand = parent->_parent;
if (parent == grand->_left)
{
Node* uncle = grand->_right;
if (uncle && uncle->_co == Red)
{
//这里只变色就好
parent->_co = uncle->_co = Black;
grand->_co = Red;
cur = grand;
parent = cur->_parent;
}
else
{
if (cur == parent->_left)
{
_RotateR(grand);
grand->_co = Red;
parent->_co = Black;
}
else
{
_RotateL(parent);
_RotateR(grand);
cur->_co = Black;
grand->_co = Red;
}
break;
}
}
else
{
Node* uncle = grand->_left;
if (uncle && uncle->_co == Red)
{
//这里只变色就好
parent->_co = uncle->_co = Black;
grand->_co = Red;
cur = grand;
parent = cur->_parent;
}
else
{
if (cur == parent->_right)
{
_RotateL(grand);
grand->_co = Red;
parent->_co = Black;
}
else
{
_RotateR(parent);
_RotateL(grand);
cur->_co = Black;
grand->_co = Red;
}
break;
}
}
}
_root->_co = Black;
//return true;
return make_pair(iterator(newnode), true);
}map和set内
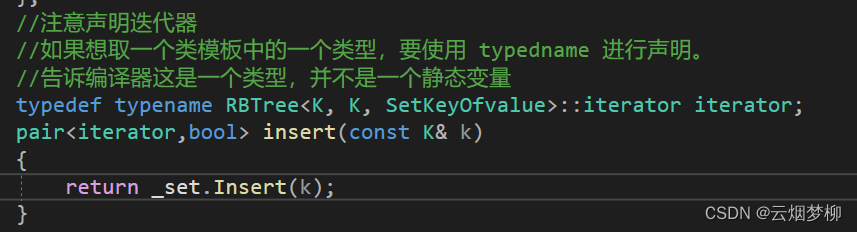
第四步,解引用返回,因为first是个迭代器类型,对其解引用返回data值
但是我们自己实现时,应该返回其data值里面的second,因为map的特性,只有second可以被修改。
故可以得出以下代码:
注意,这是定义在map里面的,并非定义在迭代器里面
V& operator[](const K& key)
{
pair<iterator, bool> result = insert(make_pair(key, V()));
//如果存在,则插入失败
//如果不存在,则插入数据
//无论是否存在,都返回 second;
return result.first->second;
}四.源代码+ 测试用例
其实map和set还有很多可以值得封装的地方,这里我们给出一个比较完整的源代码:
map:
#pragma once
#include"RBTree.h"
using namespace MyRBTree;
namespace MyMap
{
template<class K,class V>
class Map
{
public:
struct MapKeyOfvalue
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
//注意声明迭代器
//如果想取一个类模板中的一个类型,要使用 typedname 进行声明。
//告诉编译器这是一个类型,并不是一个静态变量
typedef typename RBTree<K, pair<K, V>, MapKeyOfvalue>::iterator iterator;
typedef typename RBTree<K, pair<K, V>, MapKeyOfvalue>::const_iterator const_iterator;
pair<iterator,bool> insert(const pair<K,V> &kv)
{
return _map.Insert(kv);
}
void Inorder()
{
_map.Inorder();
}
void IsBalance()
{
_map.IsBalance();
}
V& operator[](const K& key)
{
pair<iterator, bool> result = insert(make_pair(key, V()));
//如果存在,则插入失败
//如果不存在,则插入数据
//无论是否存在,都返回 second;
return result.first->second;
}
iterator begin()
{
return _map.begin();
}
iterator end()
{
return _map.end();
}
{
return _map.begin();
}
iterator end()
{
return _map.end();
}
private:
RBTree<K, pair<K,V>, MapKeyOfvalue> _map;
};
}set:
#pragma once
#include"RBTree.h"
using namespace MyRBTree;
namespace MySet
{
template<class K>
class Set
{
public:
struct SetKeyOfvalue
{
const K& operator()(const K& key)
{
return key;
}
};
//注意声明迭代器
//如果想取一个类模板中的一个类型,要使用 typedname 进行声明。
//告诉编译器这是一个类型,并不是一个静态变量
typedef typename RBTree<K, K, SetKeyOfvalue>::const_iterator iterator;
typedef typename RBTree<K, K, SetKeyOfvalue>::const_iterator const_iterator;
pair<iterator,bool> insert(const K& k)
{
return _set.Insert(k);
}
void Inorder()
{
_set.Inorder();
}
void IsBalance()
{
_set.IsBalance();
}
private:
RBTree<K, K, SetKeyOfvalue> _set;
};
} 红黑树:
#pragma once
#include<iostream>
using namespace std;
namespace MyRBTree
{
enum Color
{
Red,
Black
};
//直接实现kv模型的红黑树
template<class T>
struct RBTreeNode
{
RBTreeNode(const T& data)
:_co(Red)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
{}
Color _co;
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
T _data;
};
// 节点数据 引用/const引用 指针/const指针
template <class T, class Ref, class Ptr>
struct _RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef _RBTreeIterator<T, Ref, Ptr> self;
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &_node->_data;
}
bool operator==(const self& s)
{
return _node == s._node;
}
bool operator!=(const self& s)
{
return _node != s._node;
}
self& operator++() //迭代器++,依旧返回迭代器
{
//如果右子树存在
if (_node->_right)
{
Node* left = _node->_right;
//则寻找右子树的最左节点
while (left->_left)
{
left = left->_left;
}
_node = left;
}
//如果右子树不存在
else
{
//找孩子不是父亲右节点的节点
Node* parent = _node->_parent;
Node* cur = _node;
//一定要先判断parent是否存在,以此来避免越界
while (parent&&cur == parent->_right)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
//迭代器后置++
self operator++(int)
{
self it(_node);
++(*this);
return it;
}
self& operator--()
{
//如果左子树存在
if (_node->left)
{
//找左子树的最右节点
Node* right = _node->_left;
while (right->_right)
{
right = right->_right;
}
_node = right;
}
//如果左子树不存在
else
{
//找孩子不是父亲左节点的节点
Node* parent = _node->parent;
Node* cur = _node;
while (parent&&parent->_left == cur)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
//后置--
self operator--(int)
{
self it(_node);
--(*this);
return it;
}
_RBTreeIterator(Node* node)
:_node(node)
{}
Node* _node;
};
template<class K, class T, class KeyOfValue>
class RBTree
{
public:
typedef RBTreeNode<T> Node;
typedef _RBTreeIterator<T, T&, T*> iterator;
typedef _RBTreeIterator<T, const T&, const T*> const_iterator;
iterator begin()
{
Node* left = _root;
while (left && left->_left)
{
left = left->_left;
}
return iterator(left);
}
iterator end()
{
return iterator(nullptr);
}
const_iterator cbegin() const
{
Node* left = _root;
while (left && left->_left)
{
left = left->_left;
}
return const_iterator(left);
}
const_iterator cend() const
{
return const_iterator(nullptr);
}
//bool Insert(const T& data)
//pair<iterator,bool> Insert(const T& data)
pair<Node*, bool> Insert(const T& data)
//因为set中的iterator是 const迭代器,不可以转化为iterator类型,变成node在返回时可以构造出iterator和const迭代器
{
if (!_root)
{
_root = new Node(data);
_root->_co = Black;
//如果成功,返回成功节点的迭代器和true
return make_pair(_root, true);
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
//if (cur->_data.first < data.first)
if (kot(cur->_data)< kot(data))
{
parent = cur;
cur = cur->_right;
}
//else if (cur->_data.first > data.first)
else if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else
{
//return false;
return make_pair(cur, false);
}
}
cur = new Node(data);
cur->_co = Red;
//注意这里cur可能因为旋转,改变了原来的位置,所以需要提前记录一下
Node* newnode = cur;
//if (parent->_data.first < cur->_data.first)
if (kot(parent->_data) < kot(cur->_data))
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//开始判断是否需要变色
while (parent && parent->_co == Red)
{
Node* grand = parent->_parent;
if (parent == grand->_left)
{
Node* uncle = grand->_right;
if (uncle && uncle->_co == Red)
{
//这里只变色就好
parent->_co = uncle->_co = Black;
grand->_co = Red;
cur = grand;
parent = cur->_parent;
}
else
{
if (cur == parent->_left)
{
_RotateR(grand);
grand->_co = Red;
parent->_co = Black;
}
else
{
_RotateL(parent);
_RotateR(grand);
cur->_co = Black;
grand->_co = Red;
}
break;
}
}
else
{
Node* uncle = grand->_left;
if (uncle && uncle->_co == Red)
{
//这里只变色就好
parent->_co = uncle->_co = Black;
grand->_co = Red;
cur = grand;
parent = cur->_parent;
}
else
{
if (cur == parent->_right)
{
_RotateL(grand);
grand->_co = Red;
parent->_co = Black;
}
else
{
_RotateR(parent);
_RotateL(grand);
cur->_co = Black;
grand->_co = Red;
}
break;
}
}
}
_root->_co = Black;
//return true;
return make_pair(newnode, true);
}
void Inorder()
{
_Inorder(_root);
}
bool IsBalance()
{
return _IsBalance();
}
Node* Find(const K& key)
{
//KeyOfValue kot;
Node* cur = _root;
while (cur)
{
//if (cur->_data.first < key)
if (kot(cur->_data) < key)
{
cur = cur->_right;
}
//else if (cur->_data.first > key)
else if (kot(cur->_data) > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
//求最左节点
Node* LeftMost()
{
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return cur;
}
//求最右节点
Node* RightMost()
{
Node* cur = _root;
while (cur && cur->_right)
{
cur = cur->_right;
}
return cur;
}
private:
bool _IsBalance()
{
if (!_root) return true;
if (_root->_co == Red)
{
cout << "根节点为红色" << endl;
return false;
}
int BlackSum = 0;
Node* cur = _root;
while (cur)
{
if (cur->_co == Black) BlackSum++;
cur = cur->_left;
}
return _Check(_root, 0, BlackSum);
}
bool _Check(Node* root, int Blacknum, int BlackSum)
{
if (!root)
{
if (Blacknum != BlackSum)
{
cout << "某条路径黑色节点的数量不相等" << endl;
return false;
}
return true;
}
if (root->_co == Black)
{
++Blacknum;
}
if (root->_co == Red && root->_parent && root->_parent->_co == Red)
{
cout << "存在连续的红色节点" << endl;
return false;
}
return _Check(root->_left, Blacknum, BlackSum) && _Check(root->_right, Blacknum, BlackSum);
}
//直接创建一个全局变量,递归遍历的话消耗太高
//注意把前面我们更改的删除
//KeyOfValue kot;
void _Inorder(Node* root)
{
if (!root)
{
return;
}
//这里我们也要更改一下
_Inorder(root->_left);
//cout << root->_data.first << ":" << endl;
cout <<kot(root->_data) <<" ";
_Inorder(root->_right);
}
void _RotateR(Node* parent)
{
Node* SubL = parent->_left;
Node* SubLR = SubL->_right;
parent->_left = SubLR;
if (SubLR) SubLR->_parent = parent;
Node* pparent = parent->_parent;
SubL->_right = parent;
parent->_parent = SubL;
if (_root == parent)
{
_root = SubL;
SubL->_parent = nullptr;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = SubL;
}
else
{
pparent->_right = SubL;
}
SubL->_parent = pparent;
}
}
void _RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
subR->_left = parent; //将subR的左指针指向parent
Node* pparent = parent->_parent;
parent->_parent = subR;//将parent的父指针指向subR
if (subRL)
subRL->_parent = parent;
if (_root == parent) //判断parent是否是头节点
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = subR;
}
else
{
pparent->_right = subR;
}
subR->_parent = pparent;
}
}
KeyOfValue kot;
Node* _root = nullptr;
};
}