当前位置：首页 > article >正文

二叉树的层平均值[中等]

article 2024/9/25 21:27:27

优质博文：IT-BLOG-CN

一、题目

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

示例 1：

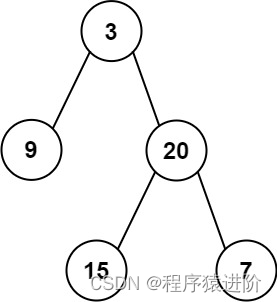
输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第0层的平均值为3,第1层的平均值为14.5,第2层的平均值为11。
因此返回[3, 14.5, 11]。

示例 2:

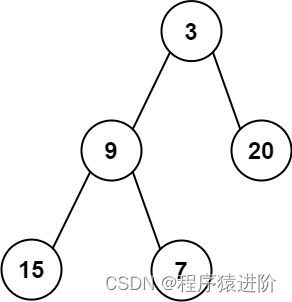
输入：root = [3,9,20,15,7]
输出：[3.00000,14.50000,11.00000]

树中节点数量在[1, 104]范围内
-231 <= Node.val <= 231 - 1

二、代码

【1】深度优先搜索： 使用深度优先搜索计算二叉树的层平均值，需要维护两个数组，counts用于存储二叉树的每一层的节点数，sums用于存储二叉树的每一层的节点值之和。搜索过程中需要记录当前节点所在层，如果访问到的节点在第i层，则将counts[i]的值加1，并将该节点的值加到sums[i]。遍历结束之后，第i层的平均值即为sums[i]/counts[i]。

class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Integer> counts = new ArrayList<Integer>();
        List<Double> sums = new ArrayList<Double>();
        dfs(root, 0, counts, sums);
        List<Double> averages = new ArrayList<Double>();
        int size = sums.size();
        for (int i = 0; i < size; i++) {
            averages.add(sums.get(i) / counts.get(i));
        }
        return averages;
    }

    public void dfs(TreeNode root, int level, List<Integer> counts, List<Double> sums) {
        if (root == null) {
            return;
        }
        if (level < sums.size()) {
            sums.set(level, sums.get(level) + root.val);
            counts.set(level, counts.get(level) + 1);
        } else {
            sums.add(1.0 * root.val);
            counts.add(1);
        }
        dfs(root.left, level + 1, counts, sums);
        dfs(root.right, level + 1, counts, sums);
    }
}

时间复杂度： O(n)，其中n是二叉树中的节点个数。深度优先搜索需要对每个节点访问一次，对于每个节点，维护两个数组的时间复杂度都是O(1)，因此深度优先搜索的时间复杂度是O(n)。遍历结束之后计算每层的平均值的时间复杂度是O(h)，其中h是二叉树的高度，任何情况下都满足h≤n。因此总时间复杂度是O(n)。
空间复杂度： O(n)，其中n是二叉树中的节点个数。空间复杂度取决于两个数组的大小和递归调用的层数，两个数组的大小都等于二叉树的高度，递归调用的层数不会超过二叉树的高度，最坏情况下，二叉树的高度等于节点个数。

【2】广度优先搜索： 也可以使用广度优先搜索计算二叉树的层平均值。从根节点开始搜索，每一轮遍历同一层的全部节点，计算该层的节点数以及该层的节点值之和，然后计算该层的平均值。如何确保每一轮遍历的是同一层的全部节点呢？我们可以借鉴层次遍历的做法，广度优先搜索使用队列存储待访问节点，只要确保在每一轮遍历时，队列中的节点是同一层的全部节点即可。具体做法如下：
1、初始时，将根节点加入队列；
2、每一轮遍历时，将队列中的节点全部取出，计算这些节点的数量以及它们的节点值之和，并计算这些节点的平均值，然后将这些节点的全部非空子节点加入队列，重复上述操作直到队列为空，遍历结束。

由于初始时队列中只有根节点，满足队列中的节点是同一层的全部节点，每一轮遍历时都会将队列中的当前层节点全部取出，并将下一层的全部节点加入队列，因此可以确保每一轮遍历的是同一层的全部节点。具体实现方面，可以在每一轮遍历之前获得队列中的节点数量size，遍历时只遍历size个节点，即可满足每一轮遍历的是同一层的全部节点。

class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Double> averages = new ArrayList<Double>();
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            double sum = 0;
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode node = queue.poll();
                sum += node.val;
                TreeNode left = node.left, right = node.right;
                if (left != null) {
                    queue.offer(left);
                }
                if (right != null) {
                    queue.offer(right);
                }
            }
            averages.add(sum / size);
        }
        return averages;
    }
}

时间复杂度： O(n)，其中n是二叉树中的节点个数。广度优先搜索需要对每个节点访问一次，时间复杂度是O(n)。需要对二叉树的每一层计算平均值，时间复杂度是O(h)，其中h是二叉树的高度，任何情况下都满足h≤n。因此总时间复杂度是O(n)。
空间复杂度： O(n)，其中n是二叉树中的节点个数。空间复杂度取决于队列开销，队列中的节点个数不会超过n。