👨‍🏫🥰🥳需要机械臂相关资源的同学可以在评论区中留言哦🤖😽🦄 

指南目录📖：

🎉🎉机械臂速成小指南（零点五）：机械臂相关资源🎉🎉

机械臂速成小指南（零）：指南主要内容及分析方法

机械臂速成小指南（一）：机械臂发展概况

机械臂速成小指南（二）：机械臂的应用

机械臂速成小指南（三）：机械臂的机械结构

机械臂速成小指南（四）：机械臂关键部件之减速机

机械臂速成小指南（五）：末端执行器

机械臂速成小指南（六）：步进电机驱动器

机械臂速成小指南（七）：机械臂位姿的描述方法

机械臂速成小指南（八）：运动学建模（标准DH法）

机械臂速成小指南（九）：正运动学分析

机械臂速成小指南（十）：可达工作空间

机械臂速成小指南（十一）：坐标系的标准命名

机械臂速成小指南（十二）：逆运动学分析

机械臂速成小指南（十三）：轨迹规划概述

机械臂速成小指南（十四）：多项式插值轨迹规划

机械臂速成小指南（十五）：线性规划

机械臂速成小指南（十六）：带抛物线过渡的线性规划

机械臂速成小指南（十七）：直线规划 

机械臂速成小指南（十八）：圆弧规划

机械臂速成小指南（十九）：机械臂的电路板抓取实验

机械臂速成小指南（二十）：机械臂的位姿重复性实验

机械臂速成小指南（二十一）：几何雅可比矩阵

机械臂速成小指南（二十二）：机械臂逆运动学的数值解方法

机械臂速成小指南（二十三）：Paul方法求解机械臂运动学逆解（含matlab代码）

机械臂速成小指南（二十四）：逆运动学的雅可比方法

🦾🌏🪐以下为正文🦾🌏🪐

        几何法与代数法都属于位置级的逆运动学解法，即最终所求得的是机械臂关节位置变量的解析表达式，这些方法针对不同机械臂的具体解算过程是不一样的，而且机械臂必须满足一个必要条件,即机械臂的逆解存在解析解。前面的章节中我们已经研究过，并不是所有机械臂的逆解都存在解析解，因此，需要其他的方法求解该类机械臂的逆解。

        下面，我们来看另外一种机械臂的逆运动学解法：速度级的雅可比方法（Jacobian方法）。

 一、雅可比矩阵的定义及特点

        速度级的雅可比方法对于不同机械臂的逆解解算过程是一样的，而且不需要机械臂的逆解存在解析解，是一种通用的逆运动学求解方法。与位置级的逆运动学求解方法相比，该方法的缺点是计算量大(求雅可比矩阵)、速度慢，优点是通用性强。

        我们以一个两自由度机械臂为例，如下图所示

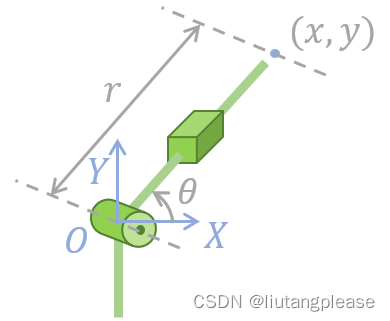
        我们首先使用几何法建立其运动学模型

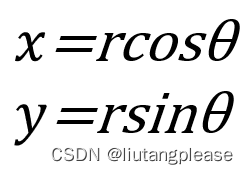
        并且r、theta≠C

         对于上列方程两边分别对时间t求导,可得

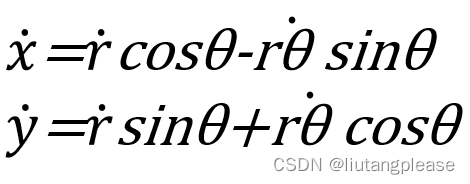
        将上式整理成矩阵形式为:

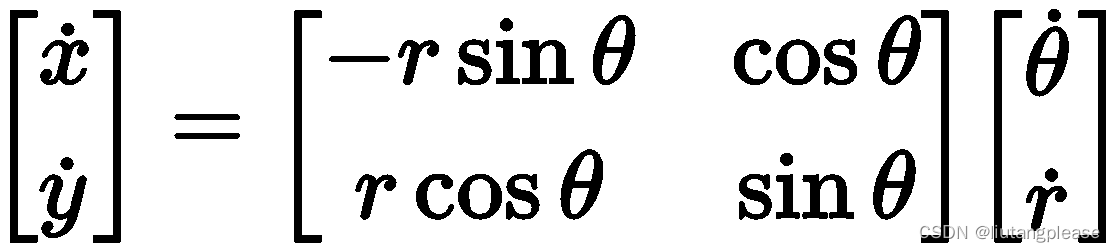
        上式中，等号左边是机械臂的末端运动速度,等号右边是机械臂的关节速度与一个矩阵
的乘积，该矩阵就是机械臂的雅可比矩阵(虚线框中)。上式可简写为：

        雅可比矩阵的数学意义是,表示从机械臂关节速度到机械臂操作速度的广义传动比或映射关系。需要注意的是,该广义传动比非定值。对于任意机械臂的雅可比矩阵可写成如下通式：

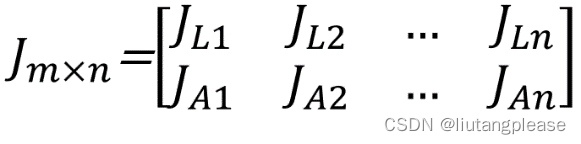
        这里，m等于机械臂工作空间的维数，n等于机械臂关节空间的维数，J_Li表示线速度的传动比，J_Ai表示角速度的传动比。

        根据m和n的数值关系，可将机械臂分成以下三种类型

1.         1. n>m：冗余度机械臂，如7自由度机械臂；
   1.         2. n=m：常规机械臂，如6自由度机械臂；
      1.         3. n＜m：欠驱动机械臂，如特殊结构的空间5自由度机械臂。

        对于常规机械臂，雅可比矩阵J是方阵，如果J满秩,可以直接利用公式

        进行逆解计算。但不是对于所有的关节角值，J的逆都存在，在某些位形时，如果|J|=0,则机械臂处于奇异位形或奇异状态，J的逆不存在，不能直接进行逆解计算，需要采用特殊的解法。

        对于冗余机械臂和欠驱动机械臂，由于雅可比矩阵非方阵，因此需要采用特殊的矩阵阵逆方法(如广义逆法)求得雅可比矩阵的逆，由公式

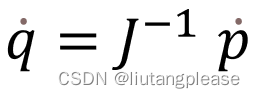
        求得机械臂逆解的特解。

        机械臂的雅可比矩阵有下列特点：

1. 平面机械臂的雅可比矩阵最多有 3 行；
2. 空间机械臂的雅可比矩阵最多有6行；
3. 具有n个关节的空间机械臂的雅可比矩阵是6Xn阶；
4. 雅可比矩阵的前3行代表线速度的传递，后3行代表角速度的传递；
5. 雅可比矩阵的每一列代表对应的关节速度对机械臂末端线速度和角速度的影响。

        将雅可比矩阵写成分块的形式，则机械臂末端的线速度和角速度可以表示成各个关节速度的线性函数。