简单介绍一些其他的树

目录

N叉树（N-ary Tree）:

B树（B-tree）:

B+树（B+ Tree）:

AVL树（AVL Tree）:

红黑树（Red-Black Tree）:

Trie树（Trie Tree）:

树堆（Treap）:

最小生成树（Minimum Spanning Tree，MST）:

区间树（Interval Tree）:

优缺点

B与B+树

B树（B-tree）：

优点：

缺点：

B+树（B+ Tree）：

优点：

缺点：

AVL树（AVL Tree）:

优点：

缺点：

红黑树（Red-Black Tree）:

优点：

缺点：

Trie树（Trie Tree）:

优点：

缺点：

区间树（Interval Tree）:

优点：

缺点：

我的其他博客

除了二叉树之外，存在许多不同类型的树，这些树在计算机科学和其他领域中都有广泛的应用。以下是一些常见的树结构：

1. N叉树（N-ary Tree）:

   • 特点： 每个节点可以有多于两个的子节点。
   • 应用： 常见于文件系统、组织结构等场景，例如Unix文件系统。

2. B树（B-tree）:

   • 特点： 平衡搜索树，节点可以包含多个键和子节点。用于数据库和文件系统。
   • 应用： 数据库索引、文件系统、存储引擎等，B树通过保持树的平衡来提高检索性能。

3. B+树（B+ Tree）:

   • 特点： B树的变种，数据存储在叶子节点上，非叶子节点仅包含键值。提高范围查询性能。
   • 应用： 数据库索引，特别是用于范围查询的场景。

4. AVL树（AVL Tree）:

   • 特点： 自平衡二叉搜索树，通过旋转操作保持树的平衡，任何节点的两个子树高度最多相差1。
   • 应用： 数据库索引、实时系统中需要快速搜索的场景。

5. 红黑树（Red-Black Tree）:

   • 特点： 自平衡二叉搜索树，引入颜色信息，保持平衡。常用于实现关联容器。
   • 应用： C++的std::map和std::set等标准库实现。

6. Trie树（Trie Tree）:

   • 特点： 也称前缀树，用于存储动态集或关联数组，高效地支持字符串的插入、删除和查找。
   • 应用： 字典、拼写检查、自动补全等字符串相关的应用。

7. 树堆（Treap）:

   • 特点： 随机化搜索树，同时满足二叉堆和二叉搜索树的性质。节点包含键值和随机优先级。
   • 应用： 用于高效地维护一个动态集合，支持快速的插入、删除和查找。

8. 最小生成树（Minimum Spanning Tree，MST）:

   • 特点： 无环连通子图，包含所有顶点，所有边权重之和最小。
   • 应用： 网络设计、电缆布线、图像分割等，Prim和Kruskal算法常用于求解最小生成树。

9. 区间树（Interval Tree）:

   • 特点： 用于存储和搜索包含一维区间的数据结构，通常实现为平衡搜索树。
   • 应用： 时间调度、数据库查询、地理信息系统等需要区间查询的场景。

这只是树结构的一小部分，还有许多其他类型的树在不同的应用中得到应用。每种树结构都有其独特的性质，适用于特定的问题和场景

优缺点

B与B+树

B树（B-tree）：

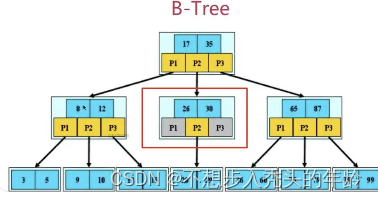
优点：

1. 高度平衡： B树是一种自平衡树，保持较低的高度，确保基本操作（插入、删除、查找）的性能较稳定。

2. 适应性强： B树适用于磁盘和内存等各种存储介质，因为它的节点数量相对较少，每个节点可以包含多个键和子节点。

3. 范围查询效率： B树在范围查询上的性能相对较好，因为每个节点都包含一定范围的键，减少了遍历的次数。

缺点：

1. 非常规节点： 节点的结构相对复杂，包含多个键和子节点，因此实现和维护相对复杂。

2. 可能引发频繁的分裂和合并： 插入和删除操作可能导致节点的分裂和合并，增加了管理的复杂性。

B+树（B+ Tree）：

优点：

1. 有序存储： B+树的叶子节点形成有序链表，有助于范围查询和遍历。

2. 高度平衡： 类似于B树，B+树保持相对平衡的高度，保证了良好的性能。

3. 适合范围查询： B+树对范围查询的支持更好，由于数据仅存在于叶子节点，范围查询可以直接沿着链表进行。

4. 适用于大规模数据库： 在大规模数据库中，B+树的性能通常优于B树。

缺点：

1. 非适应性： 对于单个查询，B+树的性能可能略逊于B树，因为B+树的节点链表可能导致额外的指针遍历。

2. 不适合随机查询： 在执行单个查找时，B+树的性能可能不如B树，因为需要通过链表遍历叶子节点。

AVL树（AVL Tree）:

优点：

1. 自平衡性： AVL树保持平衡，确保查询操作的时间复杂度是稳定的，不容易退化成链表。

缺点：

1. 维护成本高： AVL树在插入和删除操作时需要进行旋转操作，增加了维护成本。

2. 内存开销大： 相对于其他树结构，AVL树需要额外的平衡信息，导致内存开销较大。

红黑树（Red-Black Tree）:

优点：

1. 相对平衡： 红黑树的自平衡性较AVL树更为灵活，对于某些应用而言，维护成本较低。

2. 较低的维护成本： 插入和删除操作中的旋转次数较少，相比AVL树更容易维护。

缺点：

1. 相对不那么平衡： 与AVL树相比，红黑树在保持平衡时高度可能相对较高，导致查询操作的性能略逊于AVL树。

Trie树（Trie Tree）:

优点：

1. 高效的字符串操作： Trie树适用于大量字符串的插入、删除和查询操作。

2. 前缀搜索： 可以轻松实现前缀搜索，查找具有相同前缀的所有字符串。

缺点：

1. 内存开销大： Trie树的空间复杂度较高，对于存储大量字符串可能会导致内存开销较大。

区间树（Interval Tree）:

优点：

1. 高效的区间查询： 区间树适用于需要高效处理区间重叠查询的应用场景。

缺点：

1. 构建和维护成本高： 区间树的构建和维护相对较复杂，可能需要更多的时间和资源。

我的其他博客

HTTP与HTTTPS的区别-CSDN博客

什么情况下会产生StackOverflowError（栈溢出）和OutOfMemoryError（堆溢出）怎么排查-CSDN博客

谈谈我对HashMap扩容机制的理解及底层实现-CSDN博客

Redis 两种持久化方式 AOF 和 RDB-CSDN博客MySQL中的锁（简单）-CSDN博客

JDK、JRE、JVM的特点和关联-CSDN博客

面向对象的三大特征-CSDN博客

雪花算法生成id-CSDN博客

浅谈开源和闭源的认知-CSDN博客

浅谈开源和闭源的认知-CSDN博客

TCP三次握手 四次挥手-CSDN博客