维基百科文章爬虫和聚类:高级聚类和可视化

一、说明
维基百科是丰富的信息和知识来源。它可以方便地构建为带有类别和其他文章链接的文章,还形成了相关文档的网络。我的 NLP 项目下载、处理和应用维基百科文章上的机器学习算法。
在我的上一篇文章中,KMeans 聚类应用于一组大约 300 篇维基百科文章。如果没有任何预期的标签,则只能通过检查哪些文章被分组在一起以及哪个单词最常出现来接近聚类结果。结果并不令人信服,例如有关人工智能的文章与有关太空探索的文章归为一类。
为了提高聚类结果,本文实现了三个不同的目标。首先,可视化文档矢量化结果并绘制聚类。其次,应用不同的矢量化方法。第三,使用额外的聚类算法。
本文的技术背景是Python v3.11和scikit-learn v1.2.2。所有示例也应该适用于较新的库版本。
本文最初出现在我的博客admantium.com上。
二、相关境况
本文是有关使用 Python 进行 NLP 的博客系列的一部分。在我之前的文章中,我介绍了如何使用该WikipediaReader对象从“机器学习”、“航天器”和“Python(编程语言)”文章中下载 100 个子页面,创建了约 300 篇文章的语料库。这些文章,仅仅是文本文件,由一个对象进一步处理WikipediaCorpus,以总结所有文章的整体。然后创建一个 Pandas DataFrame 对象,其中包含每篇文章的标题、文本、预处理文本和标记。最后,将预处理后的文本矢量化并用作聚类算法的输入。
2.1 目标 1:可视化
第一个目标是更好地理解文档的向量空间。在到目前为止的文章系列中,使用 SciKit Learn 内置的 .zip 文件将词袋词典转换为向量DictVectorizer。以下代码片段显示了它的应用并给出了对结果向量的印象:
from sklearn.feature_extraction import DictVectorizer
vectorizer = DictVectorizer(sparse= False )
x_train = vectorizer.fit_transform(X[ 'bow' ])
print ( type (x_train))
#numpy.ndarray
print (x_train)
#[[ 15. 0. 10 . ... 0.0.0.]
# [662. 0. 430. ... 0. 0. 0.]
# [316. 0.143....0.0.0.]
#...
#[319. 0.217. ... 0.0.0.]
# [158. 0.147. ... 0.0.0.]
# [328. 0. 279. ... 0. 0. 0.]]
print (x_train.shape)
# (272, 52743)
print (vectorizer.get_feature_names_out())
# array([',', ',1', '. ', ..., 'zy', 'zygomaticus', 'zygote'], dtype=object)
print ( len (vectorizer.get_feature_names_out()))
# 52743如您所见,生成的向量有 52743 个维度。
为了绘制它们,我们将使用 PCA 进行降维,然后绘制它。通过以下代码实现对训练数据应用 2D PCA,然后绘制绘图:
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
def pca_reduce ( vec_list,dimensions= 2 ):
return PCA(dimensions).fit_transform(vec_list)
def d2_plot ( data ):
plt.plot(data, 'o' )
d2_plot( pca_reduce(x_train, 2 ))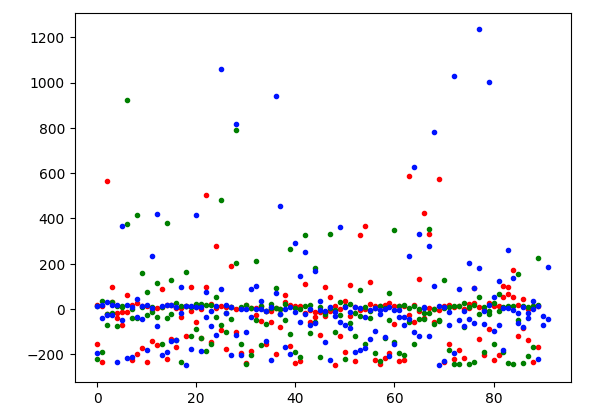
数据点没有明显的分离,它们或多或少以 y 轴为中心,具有零值和一些异常值。当使用另一种降维机制时,这个图会改变吗?
以下代码将TruncatedSVD应用于数据。
import matplotlib.pyplot as plt
from sklearn.decomposition import TruncatedSVD
def pca_reduce ( vec_list,dimensions= 2 ):
return TruncatedSVD(dimensions, n_iter= 40 ).fit_transform(vec_list)
def d2_plot ( data ):
plt.plot(data, '. ' )
d2_plot(pca_reduce(x_train, 2 ))该图看起来有点不同,y 轴上值小于 0 的异常值较少。
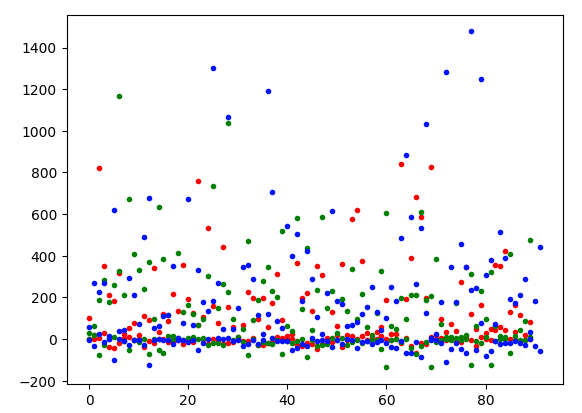
最后,让我们以 3D 图表的形式查看数据。
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
def pca_reduce ( vec_list,dimensions ):
return PCA(dimensions).fit_transform(vec_list)
def d3_plot ( data ):
Fig = plt.figure()
ax = Fig.add_subplot(projection = '3d' )
for _, v in enumerate (data[: 90 ]):
ax.scatter(v[ 0 ],v[ 1 ], v[ 2 ],marker= '.' , color= 'r' )
for _, v in enumerate (data[ 90 : 180 ]):
ax.scatter(v[ 0 ],v[ 1 ], v[ 2 ],marker= '.' , color= 'g' )
for _, v在 enumerate (data[ 180 :]) 中:
ax.scatter(v[ 0 ],v[ 1 ], v[ 2 ],marker = '.' , color= 'b' )
plt.show()
d3_plot(pca_reduce( x_train, 3 ))在此图中,数据点也非常密切相关。
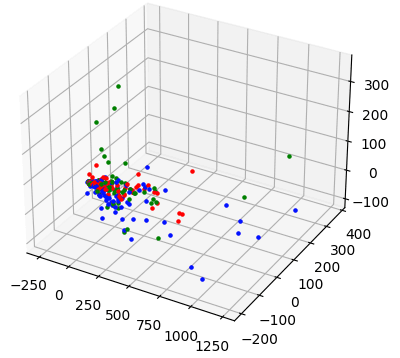
这些可视化显示了使用词袋文档表示的一个明显缺点:生成的向量彼此接近,使得聚类算法难以正确分离文档。为了更好地区分数据,我们需要使用另一种向量化方法并直观地比较得到的向量空间。
2.2 目标 2:应用不同的矢量化方法
假设更改向量化方法可以导致更好的分离向量,从而获得更好的聚类,本节介绍两种不同的向量化方法:Tfidf 和 WordVectors。
2.2.1 Tfidf矢量化
SciKit Learn 具有内置的 Tfidf Vector,可应用于原始文本数据。preprocessed在该项目的设置过程中,生成了原始数据的特殊表示,其中所有单词都表示为其引理,并且删除了大多数停用词。将根据该数据计算 Tfidf 向量。
这是相关代码:
from sklearn.feature_extraction.text import TfidfVectorizer
x_train = X['preprocessed'].tolist()
vectorizer = TfidfVectorizer()
x_train = vectorizer.fit_transform(x_train)
print(x_train.shape)
# (272, 40337)
print(x_train)
# (0, 1002) 0.010974360184074128
# (0, 5031) 0.011294684416460914
# (0, 30935) 0.013841666362619034
# (0, 1004) 0.010228010133798603
# (0, 22718) 0.009819505656781956
# (0, 1176) 0.012488241517746365
# (0, 4398) 0.012488241517746365
# (0, 8803) 0.015557383558602929
# (0, 36287) 0.028985349686940432生成的向量空间只有 40337 维。对结果向量应用 2D 和 3D PCA 得出以下图表:
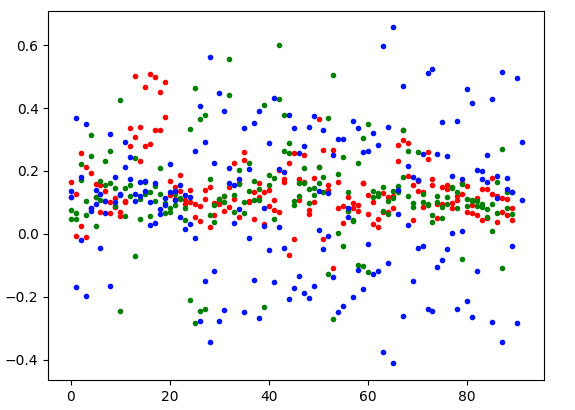
2D 图表显示了数据点之间更清晰的分离,而在 3D 图表中,我们看到红色和绿色标记点之间存在一些差异。
2.2.2 词向量向量化
词向量用多维值表示每个词,该多维值表示其在训练的语料库材料的上下文中的含义。正如前面的文章所述,存在不同的预训练词向量表示,Gensim 库提供它们方便的下载。
在以下示例中,使用具有 50 个维度的 Glove Gigaword 预训练向量。DataFrame 对象已经定义了一个token从预处理文本派生的列表(只有引理,没有停用词),并从中创建一个包含单词向量的新列。
import gensim.downloader as api
import numpy as np
vocab = corpus.vocab()
vector_lookup = api.load('glove-wiki-gigaword-50')
word_vector(tokens):
return np.array([
vector_lookup[token]
for token in tokens
if token in vocab and token in vector_lookup
])
X['word_vector'] = X['tokens'].apply(lambda tokens: word_vector(tokens))运行此代码会生成以下增强的 DataFrame 对象:
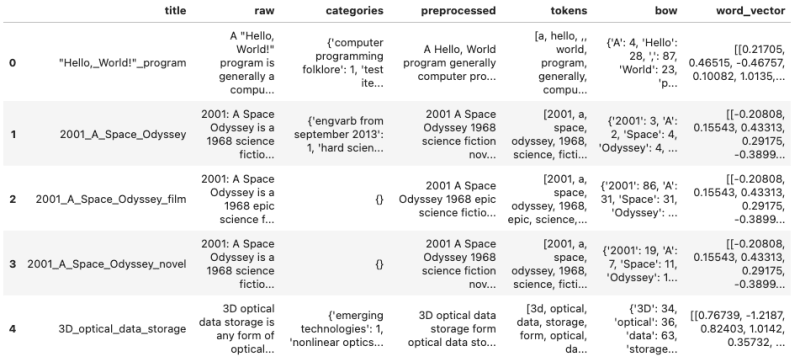
在目前的形式中,词向量具有不同的长度。详细打印它们的长度并绘制直方图是通过以下代码实现的:
word_vector_length = np.array([len(tokens) for tokens in X['word_vector'].to_numpy().flatten()])
print(word_vector_length[:5])
# [760, 157, 7566, 2543, 2086]
bins=int(np.max(word_vector_length)/1000)
plt.hist(x=word_vector_length, bins=bins, density=False)
plt.show()
print(f'Mean: {word_vector_length.mean()}')
# Mean: 2248.904411764706直方图清楚地表明较短的文章文本是常态:
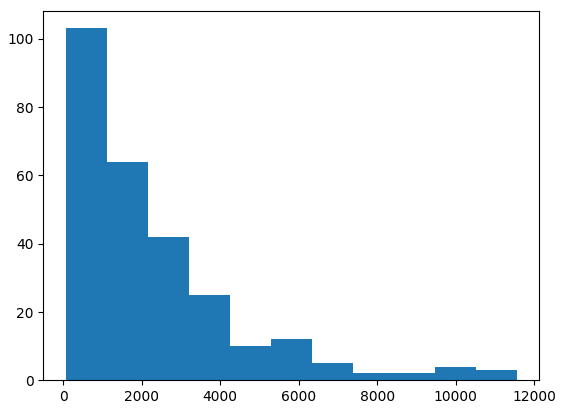
要应用 PCA,需要填充和截断向量。我选择最大字长为 6000,这意味着填充/截断为 300000。
def pad_word_vectors(vec_list, padding_value):
res = []
for vec in vec_list:
con = np.array([v for v in vec]).reshape(-1)
con_padded = np.pad(con, (0, padding_value))
con_truncated = con_padded[:padding_value]
res.append(con_truncated)
return np.array(res)
def pca_reduce(vec_list, n_components):
return PCA(n_components).fit_transform(vec_list)
X = pd.read_pickle('ml29_01_word_vectors.pkl')
x_train = X['word_vector'].to_numpy()
x_train_padded = pad_word_vectors(x_train,300000)
x_train_2d = pca_reduce(x_train_padded,2)
x_train_3d = pca_reduce(x_train_padded,3)截断和填充的向量表示为 2D 和 3D 向量:
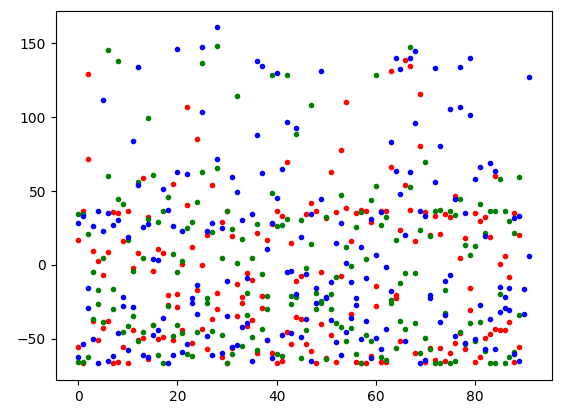
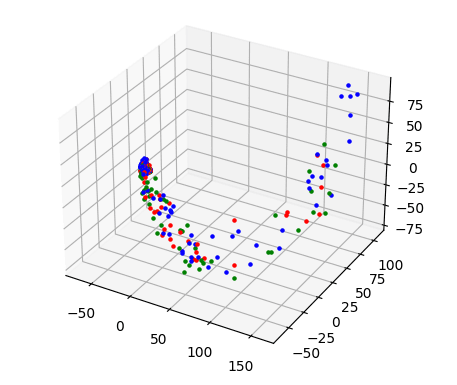
两张图都显示了数据点的清晰分离。
总结一下:DictVectorizer词袋的首字母使文档彼此非常接近。使用 Tfidf,尤其是 WordVectors 显然可以更好地分发文档。
2.3 目标 3:应用聚类算法
KMeans 只是众多聚类算法中的一种。根据这篇关于主题建模的博客文章的建议,应该根据数据的可分离程度来选择聚类算法。例如,K 均值适用于小数据集上的低维值,而当簇的密度和大小可变且数据通常为高维时,基于密度的空间聚类 (DBSCAN) 效果更好。这两种方法都创建平面集群,而另一组算法创建层次集群,例如Ward或由HDBSCAN Paython 库实现的基于层次密度的空间聚类方法。
基于此,我决定使用DBSCAN和OPtics算法,文档称其更适合大型数据集。KMeans 用作基线。
2.3.1 使用 Tfidf 向量进行聚类
KMeans 与 Tfidf
使用 KMeans 时,需要预先给出预期的簇数。尝试不同的数字并检查结果文档分布是关键。
下面的代码展示了创建8个集群的结果:
model = KMeans(n_clusters=8, random_state=0, n_init="auto").fit(x_train)
print(model)
# KMeans(n_init='auto', random_state=0)
print(model.get_params())
#{'algorithm': 'lloyd', 'copy_x': True, 'init': 'k-means++', 'max_iter': 300, 'n_clusters': 8, 'n_init': 'auto', 'random_state': 0, 'tol': 0.0001, 'verbose': 0}
print(model.labels_)
#[4 6 6 6 6 4 2 4 2 4 2 4 2 2 2 2 2 2 2 2 4 4 4 4 4 4 2 4 3 4 0 6 5 6 3 2 4
# 1 4 5 4 0 1 2 1 1 2 2 0 6 2 1 2 1 5 5 2 2 7 2 5 5 5 5 5 4 4 2 4 1 2 2 2 2
# 5 2 2 2 4 0 5 5 2 6 6 2 5 0 0 5 0 1 4 4 2 5 0 2 2 2 6 6 4 6 0 0 5 2 2 4 4
# 0 0 5 1 1 1 1 6 2 0 2 2 5 4 2 4 4 4 1 2 1 2 2 2 0 4 4 4 4 2 4 3 6 3 3 7 7
# 3 3 1 2 2 2 2 4 4 1 1 4 4 2 2 2 0 2 2 4 6 6 2 4 0 0 7 6 4 6 7 2 4 6 6 1 7
# 4 1 1 1 4 7 4 4 4 4 4 6 5 7 4 4 7 2 6 4 5 6 6 6 6 6 3 4 5 1 1 5 3 3 5 1 6
# 3 3 6 1 6 6 1 1 6 6 6 6 3 3 2 3 1 3 1 3 3 6 1 6 5 6 5 3 6 6 1 3 3 3 3 5 6
# 5 6 6 3 7 2 3 2 1 4 6 3 1]视觉表示显示簇的分离不均匀:
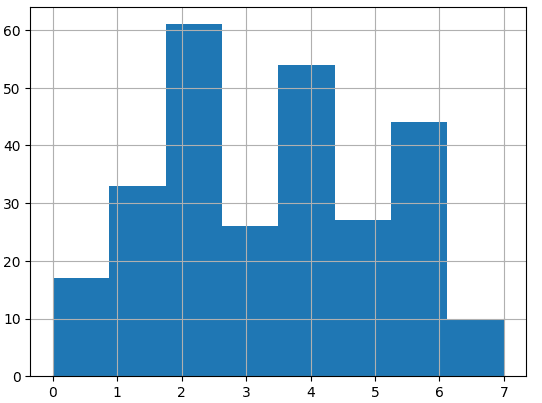
让我们尝试创建 5 个集群。
model = KMeans(n_clusters=8, random_state=0, n_init="auto").fit(x_train)
print(model.labels_)
# [0 2 2 2 4 0 2 0 4 3 3 4 3 3 3 3 3 3 3 3 0 0 0 0 0 4 3 4 4 4 3 4 2 4 4 3 4
# 4 0 2 3 0 1 3 4 2 4 3 0 4 3 1 3 2 2 2 3 3 0 3 2 2 2 4 4 4 0 3 0 2 3 3 3 3
# 1 3 3 3 4 3 1 4 3 2 2 3 2 0 0 2 0 1 4 4 3 2 0 3 2 2 2 2 0 2 2 0 1 3 2 4 0
# 0 3 4 1 1 1 1 2 3 3 3 3 4 0 3 4 0 0 1 3 1 3 3 3 3 0 0 0 0 3 0 4 2 4 4 0 0
# 4 4 4 3 3 3 3 4 0 1 1 4 0 3 3 3 3 3 3 4 1 2 3 4 0 3 0 4 4 2 0 3 0 2 1 1 0
# 4 1 1 2 4 0 0 0 0 0 0 2 2 0 0 0 0 4 4 4 2 2 2 2 1 2 4 0 2 1 1 2 4 4 4 1 2
# 4 4 2 2 2 2 2 1 4 2 2 2 4 4 3 4 1 4 1 4 4 2 2 2 2 2 2 4 4 2 2 4 4 4 4 2 2
# 2 2 2 4 0 3 4 3 2 0 4 2 1]5 个簇的直方图显示出明显的分离:
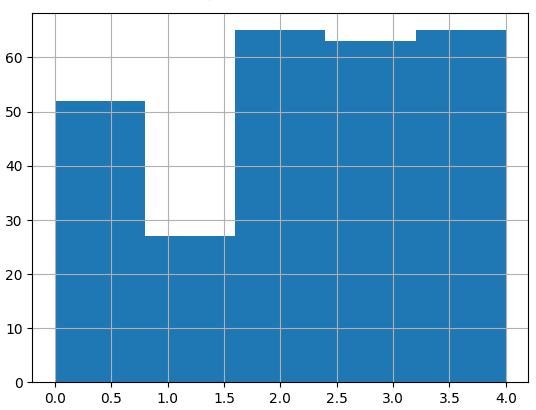
在 3D 图中绘制文档也很有前途:

2.4 DBSCAN 与 Tfidf
以下代码片段加载 pickles 数据、提取预处理文本并应用 Tfidf 矢量器。然后,通过实例化 SciKit learn 对象来创建 DBSCAN 算法。
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.cluster import DBSCAN
import pandas as pd
X = pd.read_pickle('ml29_01.pkl')
x_train = X['preprocessed'].tolist()
vectorizer = TfidfVectorizer()
x_train = vectorizer.fit_transform(x_train)使用没有任何参数化的 DBSCAN 会产生非常令人惊讶的结果:
model = DBSCAN()
print(model.get_params())
# {'algorithm': 'auto', 'eps': 0.5, 'leaf_size': 30, 'metric': 'euclidean', 'metric_params': None, 'min_samples': 5, 'n_jobs': None, 'p': None}
print(model.labels_)
# [-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# ...
# -1 -1 -1 -1 -1 -1 -1 -1]该值-1表示数据噪声太大,无法聚类。这是什么原因呢?是因为 Tfidf 向量稀疏吗?这可以通过 TruncatedSVD 来解决。
from sklearn.decomposition import TruncatedSVD
def pca_reduce(vec_list, n_components):
return TruncatedSVD(n_components).fit_transform(vec_list)
x_train_3d = pca_reduce(x_train, 3)
model = DBSCAN().fit(x_train_3d)
print(model.get_params())
# {'algorithm': 'auto', 'eps': 0.5, 'leaf_size': 30, 'metric': 'euclidean', 'metric_params': None, 'min_samples': 5, 'n_jobs': None, 'p': None}
print(model.labels_)
# [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
# 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
# ...
# 0 0 0 0 0 0 0 0 0 0 0 0 0]现在,所有文档都被放入唯一的向量中。
三、带 Tfidf 的光学器件
光学算法无法在sparseTfODF 矢量化器返回的矩阵类型上运行。需要预先通过应用 Numpy 转换方法将其转换为稠密矩阵。
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.cluster import OPTICS
X = pd.read_pickle('ml29_01.pkl')
x_train = X['preprocessed'].tolist()
vectorizer = TfidfVectorizer()
x_train = vectorizer.fit_transform(x_train).todense()应用具有一个参数的 OPTICS 算法可得出以下结果:
model = OPTICS(min_samples=10).fit(np.array(x_train))
print(model.get_params())
#{'algorithm': 'auto', 'cluster_method': 'xi', 'eps': None, 'leaf_size': 30, 'max_eps': inf, 'memory': None, 'metric': 'minkowski', 'metric_params': None, 'min_cluster_size': None, 'min_samples': 10, 'n_jobs': None, 'p': 2, 'predecessor_correction': True, 'xi': 0.05}
print(model.labels_)
#[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
# 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
# ...
# 0 0 0 0 0 0 0 0 0 0 0 0 0]不幸的是,所有文档都被再次放入一个且只有一个簇中。
四、Tfidf使用总结
使用 Tfidf 向量仅显示 KMeans 聚类的良好结果。尤其是5个簇时,可以实现明显的分离。相反,DBSCAN 和 Optics 仅将所有文档放置在同一簇中。
4.1 使用 WordVector 进行聚类-带有词向量的 KMeans
应用字向量遵循与上述相同的过程,从 DataFrame 加载其表示,然后对 300.000 个值(6000 个字)应用填充和截断。
这次,KMeans 展现了一个惊喜:当使用 300.000 长度的向量时,所有文档也被放入一个簇中:
x_train_padded = pad_word_vectors(x_train,300000)
n_clusters = 5
model = KMeans(n_clusters, random_state=0, n_init="auto").fit(x_train_padded )
print(model.labels_)
# [2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
# 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
# 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2
# 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 4 2 2 2 2
# 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2
# 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
# 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2
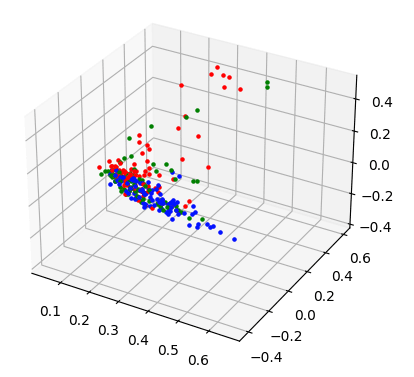
# 2 2 2 2 2 2 2 2 2 2 2 2 2]将它们简化为 3D 向量可实现良好的分离:
x_train_padded = pad_word_vectors(x_train,300000)
x_train_3d = pca_reduce(x_train_padded,3)
n_clusters = 5
model = KMeans(n_clusters, random_state=0, n_init="auto").fit(x_train_3d)
print(model.labels_)
#[0 0 1 2 2 2 2 0 0 0 0 4 0 3 0 4 0 2 4 3 4 4 1 0 3 4 0 3 4 0 0 0 4 4 4 4 0
# 4 2 0 0 0 3 2 4 4 2 3 0 4 0 3 0 3 1 2 0 0 0 0 4 0 0 1 4 2 1 1 2 1 0 0 0 0
# 0 2 2 4 0 4 0 0 2 2 3 4 4 4 0 0 0 0 2 2 4 2 1 4 1 2 2 2 3 4 1 3 0 0 3 0 4
# 4 0 0 2 1 4 2 1 4 0 0 3 0 4 2 2 2 4 1 0 0 1 4 3 0 2 3 4 4 0 4 4 2 0 2 0 0
# 4 3 1 0 0 4 0 4 2 1 2 2 3 0 0 0 4 0 0 3 0 2 0 3 0 0 0 3 0 0 0 3 0 2 4 2 0
# 3 0 0 2 4 0 3 1 0 0 4 4 3 0 0 1 0 3 4 4 1 2 0 1 0 4 3 3 2 4 0 1 1 0 0 1 3
# 3 2 3 2 4 0 4 1 4 4 0 0 4 4 4 2 4 0 0 2 2 3 1 1 2 1 1 0 0 4 1 3 4 3 3 1 2
# 1 3 3 0 3 3 4 4 4 2 0 4 1]以下是所有簇的直方图和 3D 表示:
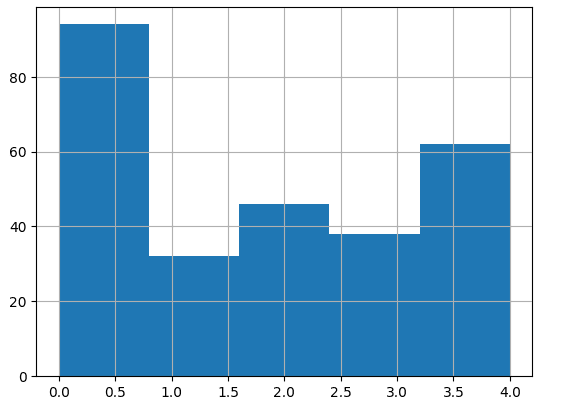
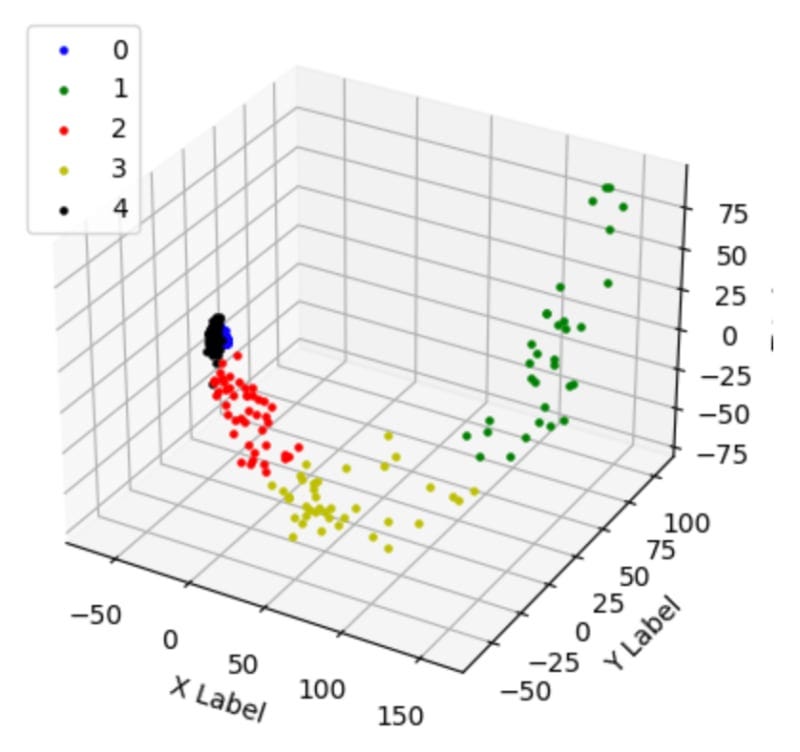
另外,让我们看看集群 1 和 5 的词云。

可以看出,集群1是关于Python、软件、系统和模型的。

第 5 组是关于航天器、卫星和太空的。这种区别对我来说看起来很有希望。
4.2 数据库扫描
让我们看看DBSCAN如何处理新的集群数据。
x_train_padded = pad_word_vectors(x_train,300000)
model = DBSCAN().fit(x_train_3d)
print(model.labels_)
# [-1 0 -1 -1 -1 -1 -1 0 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# -1 -1 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1
# 0 -1 -1 -1 0 -1 -1 -1 -1 0 0 -1 -1 0 0 -1 -1 -1 -1 -1 -1 -1 0 -1
# -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 0 0 -1 0 -1 -1
# -1 -1 -1 -1 -1 0 0 -1 0 -1 -1 -1 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1
# -1 -1 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# -1 -1 -1 -1 -1 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# -1 -1 -1 -1 -1 -1 -1 -1] 不幸的是,使用 300.000 维将所有结果放入 1 个簇中。通过 3D PCA 减少向量,一些文档仍然被检测为-1,噪声太大的数据。
为了改善 DBSCAN 结果,我尝试了不同的参数,例如DBSCAN(eps=1.0, min_samples=10, algorithm='brute',但无济于事 - 聚类结果仍然存在。另一种选择是定义自定义距离函数,但我没有在本文的范围内应用它。
五、光学
使用 300.000 维向量时,OPTICS 算法显示相同的结果:
x_train_padded = pad_word_vectors(x_train,300000)
model = OPTICS(min_samples=10).fit(np.array(x_train_padded))
print(model.labels_)
# [-1 0 -1 -1 -1 -1 -1 0 0 -1 0 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1
# -1 -1 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 0 0 -1 -1 -1 -1 -1 -1
# 0 -1 -1 -1 0 -1 -1 -1 0 0 0 -1 -1 0 0 -1 -1 -1 -1 -1 -1 -1 0 -1
# 0 -1 0 -1 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 0 -1 0 0 -1 -1 -1 -1
# -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# -1 -1 -1 0 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 0 0 -1 0 0 -1
# -1 -1 -1 -1 -1 0 0 -1 0 -1 -1 -1 -1 -1 -1 -1 0 -1 0 -1 -1 -1 -1 -1
# -1 -1 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 0
# -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# -1 -1 -1 -1 -1 -1 -1 -1 -1 0 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
# -1 -1 -1 -1 -1 0 -1 -1]但在绘制 3D 版本时,簇开始出现。
x_train_3d = pca_reduce(x_train_padded,3)
model = OPTICS(min_samples=10).fit(np.array(x_train_3d))
print(model.labels_)
# [-1 2 5 -1 -1 -1 -1 2 2 0 2 3 -1 -1 1 3 -1 -1 4 -1 4 3 5 -1
# -1 3 0 -1 4 1 2 0 -1 4 -1 -1 -1 4 -1 -1 2 2 -1 -1 -1 -1 -1 -1
# 2 -1 1 -1 2 -1 5 -1 2 2 2 1 4 2 2 5 4 -1 5 5 -1 5 2 0
# 2 0 2 -1 -1 3 0 -1 2 1 -1 -1 -1 3 3 -1 2 0 2 2 -1 -1 4 -1
# 5 -1 5 -1 -1 -1 -1 3 -1 -1 1 2 -1 -1 3 3 -1 1 -1 5 4 -1 5 3
# 2 -1 -1 0 -1 -1 -1 -1 -1 5 -1 1 5 4 -1 1 -1 -1 4 4 1 4 -1 -1
# -1 -1 -1 2 3 -1 5 1 1 4 0 -1 -1 5 -1 -1 -1 0 2 2 -1 2 2 -1
# -1 -1 -1 -1 0 2 2 -1 2 1 -1 -1 1 -1 -1 -1 2 -1 2 1 -1 4 0 -1
# 5 -1 1 3 3 -1 2 1 5 -1 -1 4 -1 -1 -1 1 5 -1 -1 -1 -1 -1 -1 2
# -1 5 -1 1 5 -1 -1 -1 -1 -1 -1 2 -1 5 4 -1 -1 1 3 -1 4 -1 -1 1
# -1 -1 -1 -1 5 5 -1 5 5 2 2 -1 5 -1 -1 -1 -1 -1 -1 -1 -1 -1 0 -1
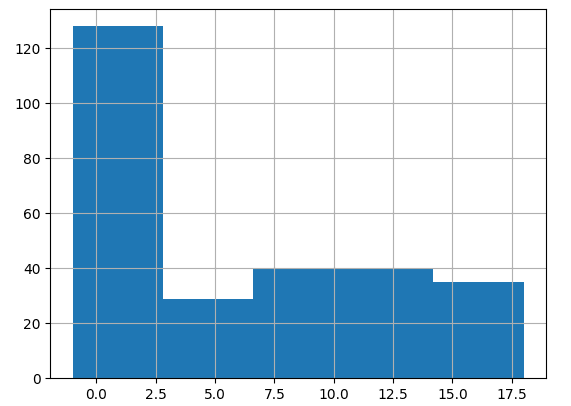
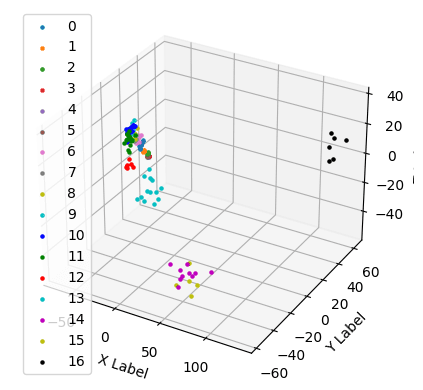
# -1 -1 -1 -1 -1 2 -1 -1]经过一些参数调整,我最终得到了以下表示:
model = OPTICS(min_samples=5, metric='minkowski').fit(np.array(x_train_3d))
print(model.get_params())
# {'algorithm': 'auto', 'cluster_method': 'xi', 'eps': None, 'leaf_size': 30, 'max_eps': inf, 'memory': None, 'metric': 'minkowski', 'metric_params': None, 'min_cluster_size': None, 'min_samples': 5, 'n_jobs': None, 'p': 2, 'predecessor_correction': True, 'xi': 0.05}
print(model.labels_)
# [-1 -1 18 -1 -1 12 -1 -1 3 -1 4 8 6 15 -1 9 6 -1 10 -1 10 8 -1 -1
# -1 8 0 16 10 -1 4 0 11 10 9 11 -1 10 13 -1 5 -1 15 13 11 9 14 -1
# 5 9 -1 15 -1 -1 -1 -1 3 5 -1 -1 10 -1 -1 18 10 -1 -1 -1 -1 -1 -1 0
# -1 0 2 14 -1 7 0 10 3 -1 14 13 -1 8 -1 9 5 0 3 3 -1 -1 10 -1
# -1 11 -1 -1 13 -1 15 -1 -1 16 -1 4 16 -1 -1 -1 -1 -1 -1 18 10 13 18 7
# 4 -1 17 -1 11 -1 -1 12 11 -1 -1 1 -1 10 -1 -1 12 17 10 10 -1 10 9 -1
# 6 12 -1 -1 7 -1 18 1 -1 11 0 -1 -1 -1 -1 14 15 0 4 4 11 5 3 -1
# -1 -1 6 16 -1 4 4 -1 -1 -1 -1 16 1 13 -1 13 5 17 2 1 13 10 0 -1
# -1 -1 1 7 8 -1 5 -1 -1 -1 15 10 9 19 13 -1 -1 -1 9 -1 -1 13 9 2
# 19 18 6 -1 -1 15 17 12 -1 13 9 2 11 -1 10 11 6 -1 8 9 10 -1 9 -1
# 7 14 12 -1 18 -1 13 18 19 4 2 -1 18 15 11 17 15 19 -1 19 -1 -1 0 -1
# 15 11 10 11 14 3 11 -1]直方图和 3D 绘图显示簇是分开的:
WordVectors 使用总结
WordVectors 产生了令人惊讶的结果。一般来说,使用 300.000 维的原始向量是不适用的:由每个文本的词序决定的数据方差太大,无法找到有意义的聚类。需要应用降维技术。然后,KMeans 再次显示出最好的分离度,其次是 OPTICS。
六、结论
文档分类结果取决于输入数据的形状以及分类算法。在将简单的词袋向量与 KMeans 结合使用时出现相当令人失望的结果后,本文将 Tfidf 和词向量与 KMeans、DBSCAN 和 Optics 结合起来。这些实验中最关键的学习点是:a)Tfidf 提供了干净的分离,无需降维即可使用,b)WordVectors 只能在降维后应用,c)KMeans 提供良好的聚类结果,无需任何参数化, d) OPTICS 也提供了很好的集群,但其参数需要调整。
