PID是控制中非常经典的一个模型，利用P(比例)、I(微分)、D(积分)三者相互合作来实现对一个信号的闭环控制，同时可以让信号波形平滑变化而不是突变。以下主要是结合一个python实现的控制速度的程序来模拟PID的过程。

参考博客：电机控制进阶——PID速度控制_pid速度控制算法_码农爱学习的博客-CSDN博客 

目录

简述 

P(比例)

I(微分)

D(积分)

基于Python的速度调整

Kp=0.01,Ki=0,Kd=0

Kp=0.01,Ki=0.01,Kd=0

Kp=0.01,Ki=0.01,Kd=0.01

简述 

    PID控制分为增量式和位置式两种控制方式，因为位置式用的比较多，因此我就以位置式的为主展开（增量式我参考的博客中有，如果有兴趣可以自行了解）。

    位置式PID控制主要由P(比例)、I(微分)、D(积分)三个部分组成，下面是一个简单的结构框图。

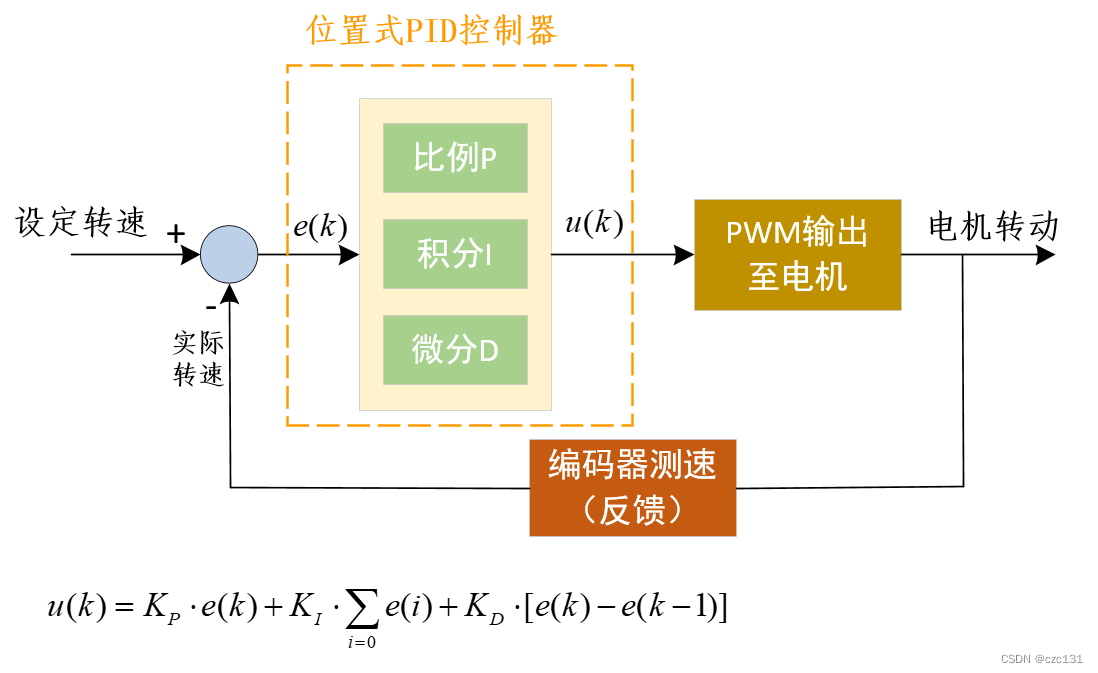
     假设当前设定的是速度，可以看到利用目标速度-实际速度，可以得到一个误差，根据这个误差经过P、I、D三种量的运算求和得到当前需要的修正量对实际值修正，然后使得最终实际值不断接近目标值。

下面是对PID单独的解释：

P(比例)

    P大致反映的改变量大小，与当前值和目标值的差距大小有关，差距越大，那么这个量也越大。      就拿推箱子举例，离目的地越远，那么你用的力也就越大，这样才能更快达到目的地，相反，要是距离目的地很近了，这时候就需要少点用力，不然就就会偏离目标更远。

I(微分)

    I大致反映的是阻力的大小，在连续情况中反映为导数，而在一般工程学的离散情况中就是两次测量误差的差值，也就是此次误差和上一次误差的差分。 

    这其实就是相当于阻力的作用， 无论你怎么调整，我都反向变化，这在最后平衡附近震荡时是很有效的，能够显著降低震荡幅度。

D(积分)

    D大致是针对不同阶段的调整做法，与调整的误差和有关。

    这个量主要是解决静态平衡的问题，假如有一个池子，有一个预期水位，有放水有漏水，一次调整周期内，放水为u，漏水为u，那么调整后水位依旧如此，下一个状态和上一个状态完全一致，那么P和I也是和上一个状态完全一致，那么调整后还是这个状态，就陷入了死循环，此时就需要D这个量，由于这个量是和误差和直接相关，那么每次调整，误差都会增加，那么下次调整的量就会和这次的不一样，就可以打破这个死循环。

基于Python的速度调整

下面主要是针对PID模型建立速度调整的模型，就以将速度从60调整至100为例，最终的精度要求是0.001，可以感受一下各个量的作用。

为了稳定的效果，我将几个系数都设置的比较小，大了很有可能就最终直接NaN了，可以自行调参设置。

代码如下：

from matplotlib import pyplot as plt

def PID(now_v,expc_v):
    Kp = 0.01
    Ki = 0
    Kd = 0
    sum_err = 0
    v_list = []
    err = expc_v - now_v
    err_last = err  # 上一次的输出,先初始化为一致
    cnt = 0
    while abs(err) > 0.001:  # 误差还在范围外
        err = expc_v - now_v
        sum_err += err
        uk = Kp*err + Ki * sum_err + Kd * (err-err_last) # 确定本次输出
        # now_v = now_v + uk + random.uniform(0,0)  # 更新当前速度,加入一个扰动
        now_v = now_v + uk
        err_last = err
        v_list.append(now_v)
        cnt += 1
    print(cnt)
    plt.plot(v_list)
    plt.show()

if __name__ == '__main__':
    PID(60,100)

Kp=0.01,Ki=0,Kd=0

此时表示的是仅利用P来控制，运行后发现下面的调整过程

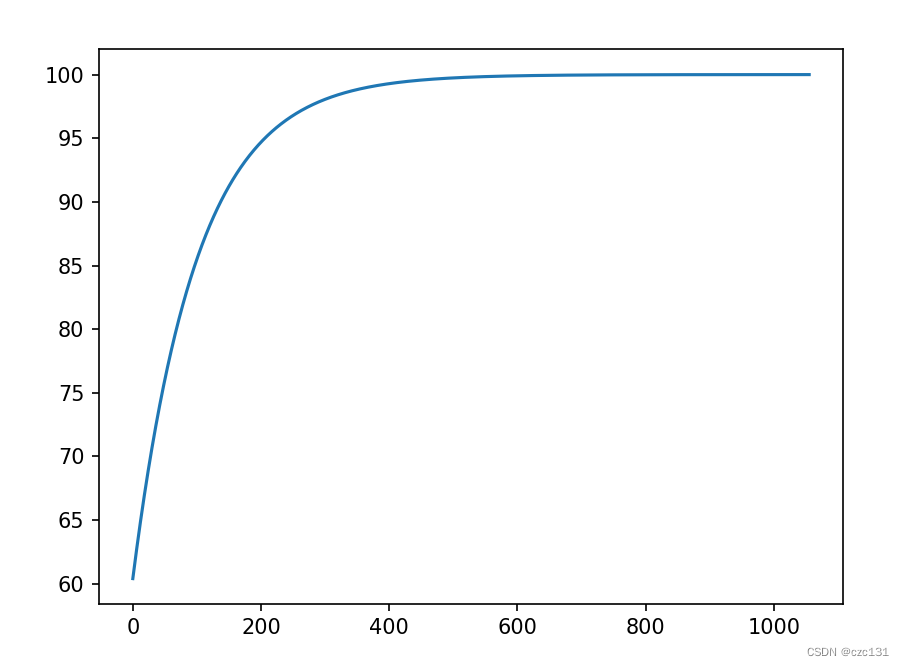
看上去非常理想，因为这种情况本身就比较理想， 如果我加入了一个扰动项，那么就会变成下面这样，将速度加入随机扰动项。

now_v = now_v + uk + random.uniform(-0.1,0.1)  # 更新当前速度,加入一个扰动

 经过测试，比较小的扰动还是可以很快收敛，但是如果扰动比较大，比如为(-2,2)，那么就会像下面这样

 到了五千轮左右才收敛，随着误差的增大，这个此时会变得更多，因此仅仅靠P来控制仅适用于理想情况。

Kp=0.01,Ki=0.01,Kd=0

此时加入了I这个量，这个量在前面说主要是为了消除震荡，可以很好消除外部的一些影响，同样设置(-2,2)的随机扰动，如下：

 发现在2500轮左右就实现了精度的要求，不过从实验来看，效果并不是很明显，可能是因为参数还没有调好。

Kp=0.01,Ki=0.01,Kd=0.01

这种情况下就是加入了累积误差项的调整，就是完整的PID过程。

还是在(-2,2)的随机误差情况下，这种组合的相对调整次数确实会少一点。

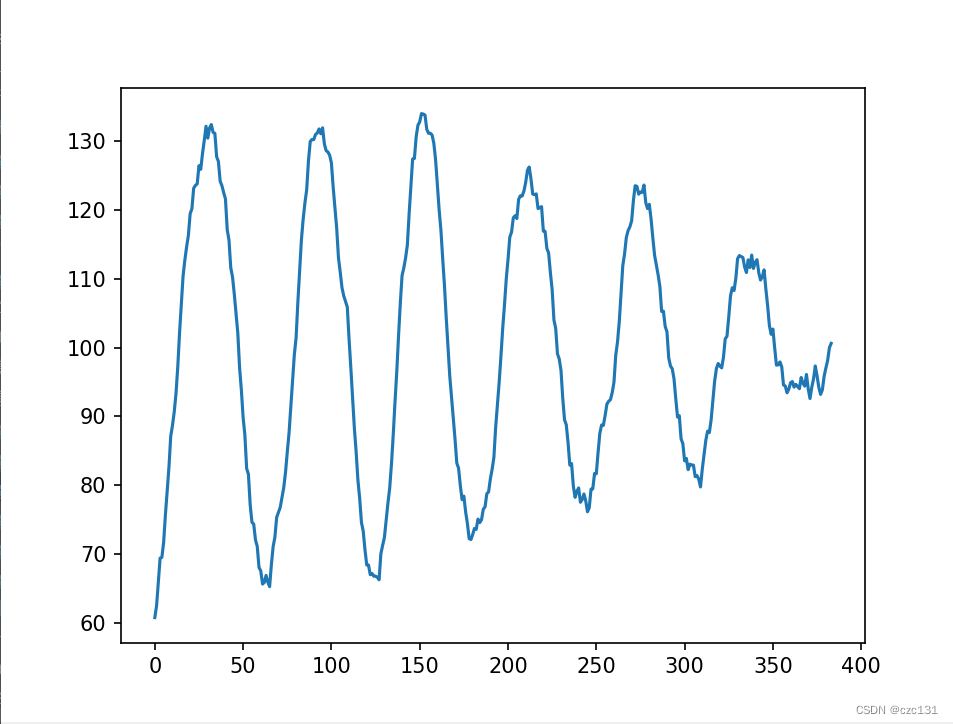
 以上就是关于PID的一些个人理解，就是简单调试，没有真正调参，就当是做个记录了。