3.3 泰勒公式例题分析
例1 写出函数f(x)=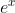
带有拉格朗日余项的n阶麦克劳林公式
我的答案：
一、信息
1.f(x)的表达式
2.目标求这个f(x)的n阶麦克劳林公式
二、分析
条件1：告诉我f(x)的表达式为我后续带入公式做准备
条件2：告诉我用什么公式和此次求解的方向
三、思考
疑问：
怎么求麦克劳林公式呢？
解答：
这就要回忆麦克劳林公式的有关记忆区域了，找到它(传送门：3.3 泰勒公式)，从记忆空间中我们发现麦克劳林的公式为：
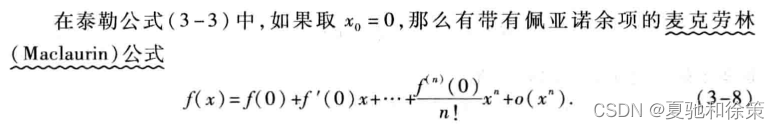
通过观察，我们发现要求这个公式其实很简单，我们只需要求f(0)的n次导数和n的阶乘即可，因此求解这个公式的问题的关键就转换成求解导数和阶乘的问题。
四、解答过程
五、演绎推理检查
为什么它的问题没有余项？
六、正确答案对比：
例2
一、信息
与例一一致
二、分析
与例一一致
三、思考
疑问：
前面都一样但是从前四次就发现f(x)的导数和例一有所不同，不仅如此在n次求导后并不确定他是那一次，那该怎么做下去呢？
解答：
这个时候就要用到分类讨论的思想了。
我们把它分为四种情况分别求出他们的麦克劳林公式
错了哈哈哈哈哈哈哈~
四、过程
五、演绎推理
六、正确答案对比
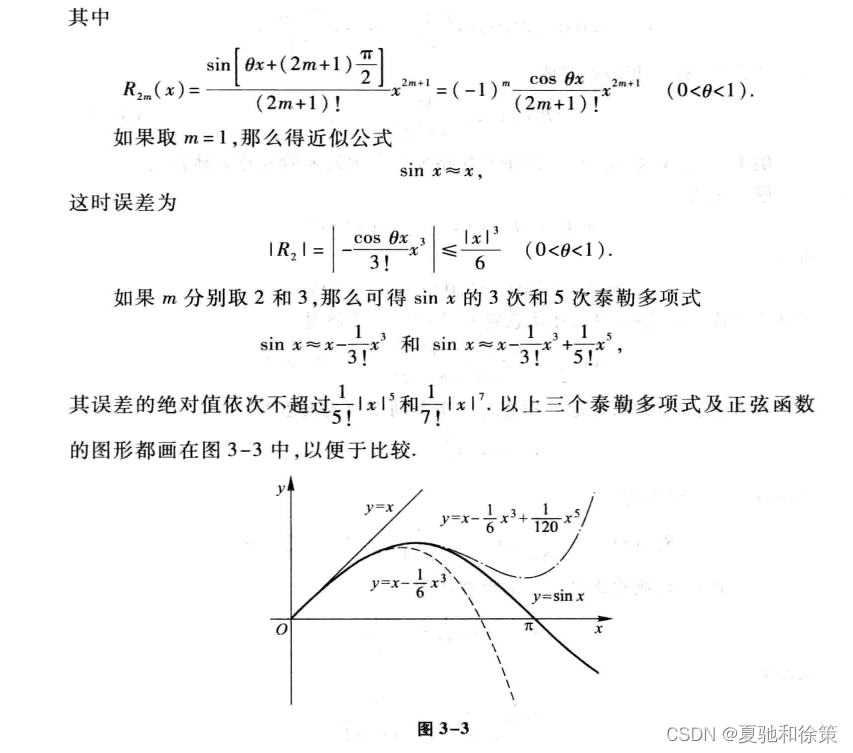
七、举一反三(理论转换实践的观念)
例三：
一、信息
1.利用有余项的麦克劳林公式求极限
2.表达式
二、分析
条件1告诉我此次要用的工具
条件2告诉我表达式
三、思考
1.麦克劳林公式带余项的，那么我们首先要回忆这个公式，
六、答案对比
