【每日一题】
文章目录
- C++ 技术点
- 多边三角形剖分的最低得分(dp思路,选不选问题)
- 移动石子到连续(思路)
C++ 技术点
1. string类型使用find函数。
int index = s.find("@");
if (inde != string:npos){
xx
}
2. transform函数,将整个字符串做整体改变。
transform(s.begin(), s.end(), s.begin(), ::tolower);
多边三角形剖分的最低得分(dp思路,选不选问题)

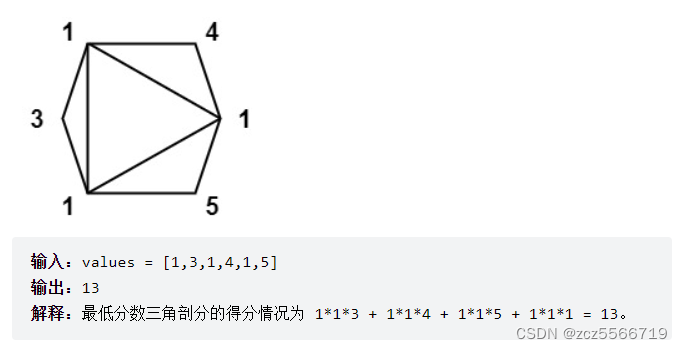
- dp定义:dp[i][j]表示点 i 到点 j 的多边形的最小值。
- dp转移:转移方程的思路两种。选不选、选哪个。现在本题只有选哪个这个思路。因此
dp[i][j] = min(dp[i][j], dp[i,k]+dp[k,j]+cal(i,j,k))。 - 枚举次序:求解dp[i][j]的时候是需要提前知道dp[i][k](k<j)这个更小的问题的,因此此时 j 是正序枚举;同样的对于dp[k][j]则是需要知道 k 才能知道 i 的,因此 i 是倒序枚举。
- dp初始值:在枚举次序分析以后,我们知道dp[i][i],dp[i][i+1] = 0, 其他的初始化为INT_MAX;
class Solution {
public:
int minScoreTriangulation(vector<int> &v) {
int n = v.size(), f[n][n];
memset(f, 0, sizeof(f));
for (int i = n - 3; i >= 0; --i)
for (int j = i + 2; j < n; ++j) {
f[i][j] = INT_MAX;
for (int k = i + 1; k < j; ++k)
f[i][j] = min(f[i][j], f[i][k] + f[k][j] + v[i] * v[j] * v[k]);
}
return f[0][n - 1];
}
};
移动石子到连续(思路)

比较有思维量的题目。首先我们需要思考下最终的结果是处于什么区间上的,也就是我们需要选在一个长度为 k 的区间最后将所有的石子搬运到这个区间上。
另外我们还需要思考,如何实现最大和最小的移动。
- 最大:以左右端点作为其中一个端点进行移动。这两个点之间的所有端点都是需要一次操作的。
- 最小:首先设计一个滑动窗,窗的两侧为实际存在的石子,并且左右两侧的石子的距离是小于 n 的最大距离。此时我们可以分情况讨论:
- 如果左右端点差为n,完全不需要动,返回0;
- 两个端点的距离差[stone[l], stone[r] ]恰好为n-1,石子数量也为n-1,也就是n-1个全部都是连续的。此时外面还剩一个,无论在什么位置,最多两次就可以连续。(认为右侧不动)
- 否则,填上中间的空挡即可。
class Solution {
public:
vector<int> numMovesStonesII(vector<int>& stones) {
int n = stones.size();
sort(stones.begin(), stones.end());
// max = max(stones[n-2] - stones[0] -1, stones[n-1]-stones[1]-1)
// min = 在一个滑动窗内 k个,因此需要n-k次
// 如果有n-1个是紧密相连的。那么 需要两次
if(stones[n-1]- stones[0]+1 == n){
return {0, 0};
}
int max_v = max(stones[n-2] - stones[0] +1, stones[n-1]-stones[1]+1)-(n-1);
int min_v = max_v;
int r = 1;
for (int l = 0;l<n;l++){
while(r < n && stones[r]-stones[l]+1 <= n){
r++;
}
r--;
// 左端点l到右端点r是连续的
if (r-l+1 == n-1 && stones[r]-stones[l]+1 == n-1){
min_v = min(min_v, 2);
}else{
min_v = min(min_v, n-(r-l+1));
}
}
return {min_v, max_v};
}
};
